Bag of Policies for Distributional Deep Exploration

Efficient exploration in complex environments remains a major challenge for reinforcement learning (RL). Compared to previous Thompson sampling-inspired mechanisms that enable temporally extended exploration, i.e., deep exploration, we focus on deep exploration in distributional RL. We develop here a general purpose approach, Bag of Policies (BoP), that can be built on top of any return distribution estimator by maintaining a population of its copies. BoP consists of an ensemble of multiple heads that are updated independently. During training, each episode is controlled by only one of the heads and the collected state-action pairs are used to update all heads off-policy, leading to distinct learning signals for each head which diversify learning and behaviour. To test whether optimistic ensemble method can improve on distributional RL as did on scalar RL, by e.g. Bootstrapped DQN, we implement the BoP approach with a population of distributional actor-critics using Bayesian Distributional Policy Gradients (BDPG). The population thus approximates a posterior distribution of return distributions along with a posterior distribution of policies. Another benefit of building upon BDPG is that it allows to analyze global posterior uncertainty along with local curiosity bonus simultaneously for exploration. As BDPG is already an optimistic method, this pairing helps to investigate if optimism is accumulatable in distributional RL. Overall BoP results in greater robustness and speed during learning as demonstrated by our experimental results on ALE Atari games.

On Over-Squashing in Message Passing Neural Networks: The Impact of Width, Depth, and Topology

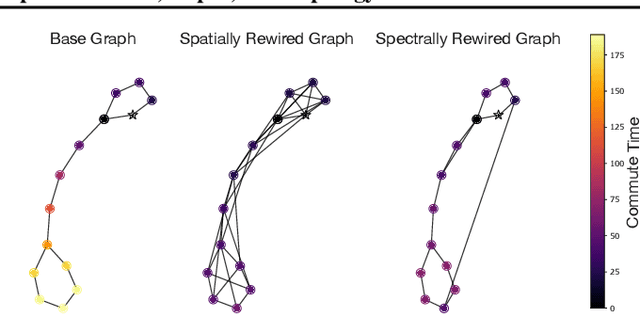
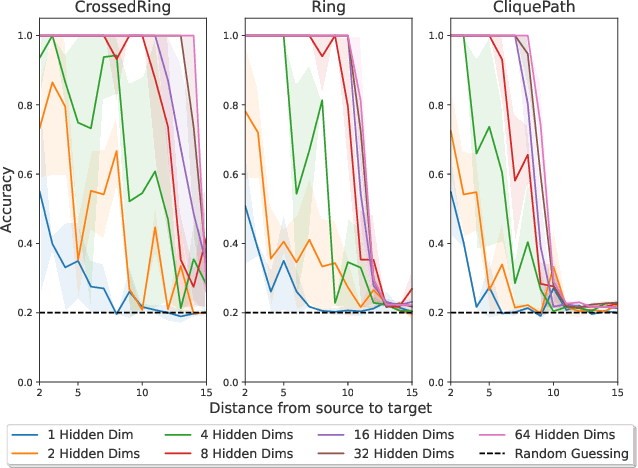
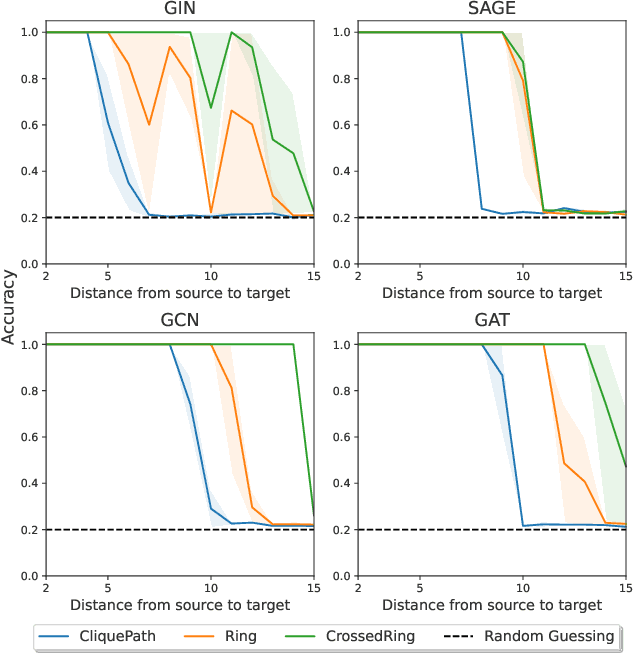
Message Passing Neural Networks (MPNNs) are instances of Graph Neural Networks that leverage the graph to send messages over the edges. This inductive bias leads to a phenomenon known as over-squashing, where a node feature is insensitive to information contained at distant nodes. Despite recent methods introduced to mitigate this issue, an understanding of the causes for over-squashing and of possible solutions are lacking. In this theoretical work, we prove that: (i) Neural network width can mitigate over-squashing, but at the cost of making the whole network more sensitive; (ii) Conversely, depth cannot help mitigate over-squashing: increasing the number of layers leads to over-squashing being dominated by vanishing gradients; (iii) The graph topology plays the greatest role, since over-squashing occurs between nodes at high commute (access) time. Our analysis provides a unified framework to study different recent methods introduced to cope with over-squashing and serves as a justification for a class of methods that fall under `graph rewiring'.

Schedule-Robust Online Continual Learning

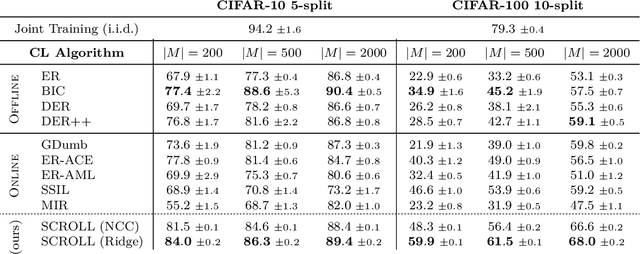
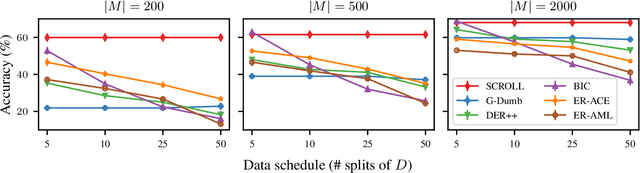
A continual learning (CL) algorithm learns from a non-stationary data stream. The non-stationarity is modeled by some schedule that determines how data is presented over time. Most current methods make strong assumptions on the schedule and have unpredictable performance when such requirements are not met. A key challenge in CL is thus to design methods robust against arbitrary schedules over the same underlying data, since in real-world scenarios schedules are often unknown and dynamic. In this work, we introduce the notion of schedule-robustness for CL and a novel approach satisfying this desirable property in the challenging online class-incremental setting. We also present a new perspective on CL, as the process of learning a schedule-robust predictor, followed by adapting the predictor using only replay data. Empirically, we demonstrate that our approach outperforms existing methods on CL benchmarks for image classification by a large margin.

Meta Optimal Transport

We study the use of amortized optimization to predict optimal transport (OT) maps from the input measures, which we call Meta OT. This helps repeatedly solve similar OT problems between different measures by leveraging the knowledge and information present from past problems to rapidly predict and solve new problems. Otherwise, standard methods ignore the knowledge of the past solutions and suboptimally re-solve each problem from scratch. Meta OT models surpass the standard convergence rates of log-Sinkhorn solvers in the discrete setting and convex potentials in the continuous setting. We improve the computational time of standard OT solvers by multiple orders of magnitude in discrete and continuous transport settings between images, spherical data, and color palettes. Our source code is available at http://github.com/facebookresearch/meta-ot.

Heterogeneous manifolds for curvature-aware graph embedding

Graph embeddings, wherein the nodes of the graph are represented by points in a continuous space, are used in a broad range of Graph ML applications. The quality of such embeddings crucially depends on whether the geometry of the space matches that of the graph. Euclidean spaces are often a poor choice for many types of real-world graphs, where hierarchical structure and a power-law degree distribution are linked to negative curvature. In this regard, it has recently been shown that hyperbolic spaces and more general manifolds, such as products of constant-curvature spaces and matrix manifolds, are advantageous to approximately match nodes pairwise distances. However, all these classes of manifolds are homogeneous, implying that the curvature distribution is the same at each point, making them unsuited to match the local curvature (and related structural properties) of the graph. In this paper, we study graph embeddings in a broader class of heterogeneous rotationally-symmetric manifolds. By adding a single extra radial dimension to any given existing homogeneous model, we can both account for heterogeneous curvature distributions on graphs and pairwise distances. We evaluate our approach on reconstruction tasks on synthetic and real datasets and show its potential in better preservation of high-order structures and heterogeneous random graphs generation.

Enabling risk-aware Reinforcement Learning for medical interventions through uncertainty decomposition

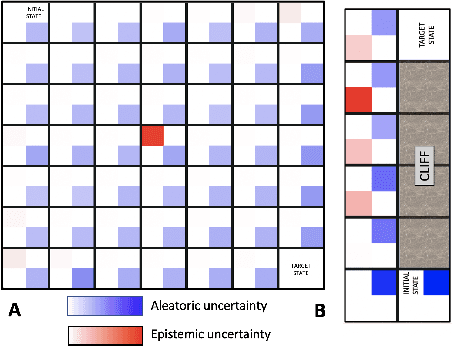
Reinforcement Learning (RL) is emerging as tool for tackling complex control and decision-making problems. However, in high-risk environments such as healthcare, manufacturing, automotive or aerospace, it is often challenging to bridge the gap between an apparently optimal policy learnt by an agent and its real-world deployment, due to the uncertainties and risk associated with it. Broadly speaking RL agents face two kinds of uncertainty, 1. aleatoric uncertainty, which reflects randomness or noise in the dynamics of the world, and 2. epistemic uncertainty, which reflects the bounded knowledge of the agent due to model limitations and finite amount of information/data the agent has acquired about the world. These two types of uncertainty carry fundamentally different implications for the evaluation of performance and the level of risk or trust. Yet these aleatoric and epistemic uncertainties are generally confounded as standard and even distributional RL is agnostic to this difference. Here we propose how a distributional approach (UA-DQN) can be recast to render uncertainties by decomposing the net effects of each uncertainty. We demonstrate the operation of this method in grid world examples to build intuition and then show a proof of concept application for an RL agent operating as a clinical decision support system in critical care

Generalization Properties of Optimal Transport GANs with Latent Distribution Learning

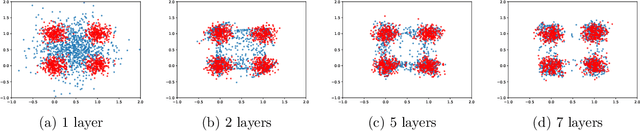
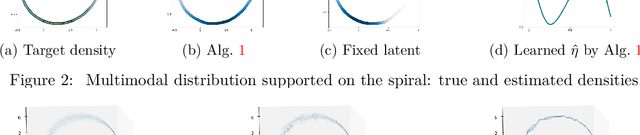
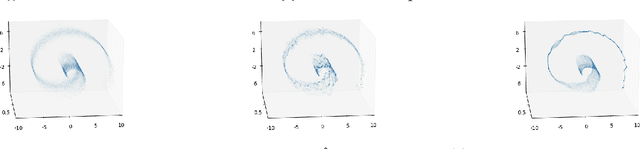
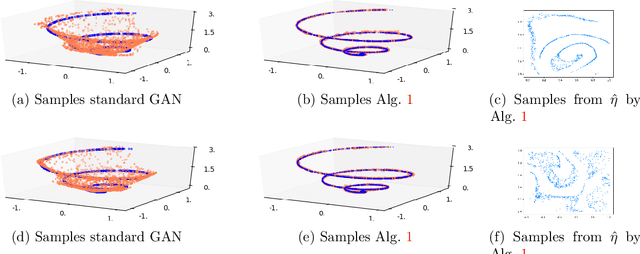
The Generative Adversarial Networks (GAN) framework is a well-established paradigm for probability matching and realistic sample generation. While recent attention has been devoted to studying the theoretical properties of such models, a full theoretical understanding of the main building blocks is still missing. Focusing on generative models with Optimal Transport metrics as discriminators, in this work we study how the interplay between the latent distribution and the complexity of the pushforward map (generator) affects performance, from both statistical and modelling perspectives. Motivated by our analysis, we advocate learning the latent distribution as well as the pushforward map within the GAN paradigm. We prove that this can lead to significant advantages in terms of sample complexity.

Aligning Time Series on Incomparable Spaces

Dynamic time warping (DTW) is a useful method for aligning, comparing and combining time series, but it requires them to live in comparable spaces. In this work, we consider a setting in which time series live on different spaces without a sensible ground metric, causing DTW to become ill-defined. To alleviate this, we propose Gromov dynamic time warping (GDTW), a distance between time series on potentially incomparable spaces that avoids the comparability requirement by instead considering intra-relational geometry. We derive a Frank-Wolfe algorithm for computing it and demonstrate its effectiveness at aligning, combining and comparing time series living on incomparable spaces. We further propose a smoothed version of GDTW as a differentiable loss and assess its properties in a variety of settings, including barycentric averaging, generative modeling and imitation learning.

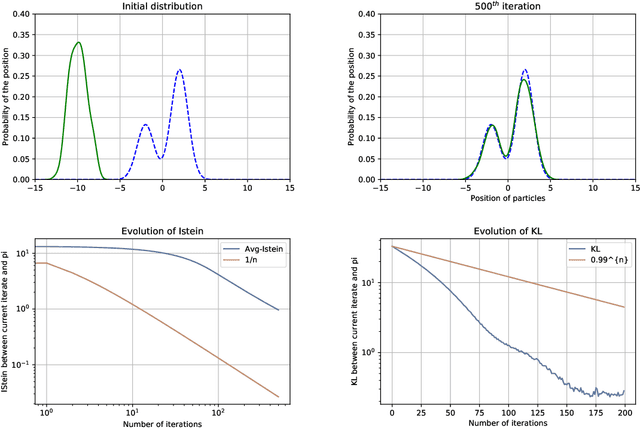
A Non-Asymptotic Analysis for Stein Variational Gradient Descent

We study the Stein Variational Gradient Descent (SVGD) algorithm, which optimises a set of particles to approximate a target probability distribution $\pi\propto e^{-V}$ on $\mathbb{R}^d$. In the population limit, SVGD performs gradient descent in the space of probability distributions on the KL divergence with respect to $\pi$, where the gradient is smoothed through a kernel integral operator. In this paper, we provide a novel finite time analysis for the SVGD algorithm. We obtain a descent lemma establishing that the algorithm decreases the objective at each iteration, and provably converges, with less restrictive assumptions on the step size than required in earlier analyses. We further provide a guarantee on the convergence rate in Kullback-Leibler divergence, assuming $\pi$ satisfies a Stein log-Sobolev inequality as in Duncan et al. (2019), which takes into account the geometry induced by the smoothed KL gradient.

Wasserstein Proximal Gradient

We consider the task of sampling from a log-concave probability distribution. This target distribution can be seen as a minimizer of the relative entropy functional defined on the space of probability distributions. The relative entropy can be decomposed as the sum of a functional called the potential energy, assumed to be smooth, and a nonsmooth functional called the entropy. We adopt a Forward Backward (FB) Euler scheme for the discretization of the gradient flow of the relative entropy. This FB algorithm can be seen as a proximal gradient algorithm to minimize the relative entropy over the space of probability measures. Using techniques from convex optimization and optimal transport, we provide a non-asymptotic analysis of the FB algorithm. The convergence rate of the FB algorithm matches the convergence rate of the classical proximal gradient algorithm in Euclidean spaces. The practical implementation of the FB algorithm can be challenging. In practice, the user may choose to discretize the space and work with empirical measures. In this case, we provide a closed form formula for the proximity operator of the entropy.