On Combining Expert Demonstrations in Imitation Learning via Optimal Transport

Imitation learning (IL) seeks to teach agents specific tasks through expert demonstrations. One of the key approaches to IL is to define a distance between agent and expert and to find an agent policy that minimizes that distance. Optimal transport methods have been widely used in imitation learning as they provide ways to measure meaningful distances between agent and expert trajectories. However, the problem of how to optimally combine multiple expert demonstrations has not been widely studied. The standard method is to simply concatenate state (-action) trajectories, which is problematic when trajectories are multi-modal. We propose an alternative method that uses a multi-marginal optimal transport distance and enables the combination of multiple and diverse state-trajectories in the OT sense, providing a more sensible geometric average of the demonstrations. Our approach enables an agent to learn from several experts, and its efficiency is analyzed on OpenAI Gym control environments and demonstrates that the standard method is not always optimal.

Optimal Transport for Offline Imitation Learning

With the advent of large datasets, offline reinforcement learning (RL) is a promising framework for learning good decision-making policies without the need to interact with the real environment. However, offline RL requires the dataset to be reward-annotated, which presents practical challenges when reward engineering is difficult or when obtaining reward annotations is labor-intensive. In this paper, we introduce Optimal Transport Reward labeling (OTR), an algorithm that assigns rewards to offline trajectories, with a few high-quality demonstrations. OTR's key idea is to use optimal transport to compute an optimal alignment between an unlabeled trajectory in the dataset and an expert demonstration to obtain a similarity measure that can be interpreted as a reward, which can then be used by an offline RL algorithm to learn the policy. OTR is easy to implement and computationally efficient. On D4RL benchmarks, we show that OTR with a single demonstration can consistently match the performance of offline RL with ground-truth rewards.

Matching Normalizing Flows and Probability Paths on Manifolds

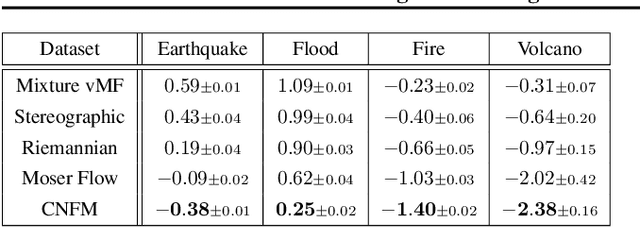
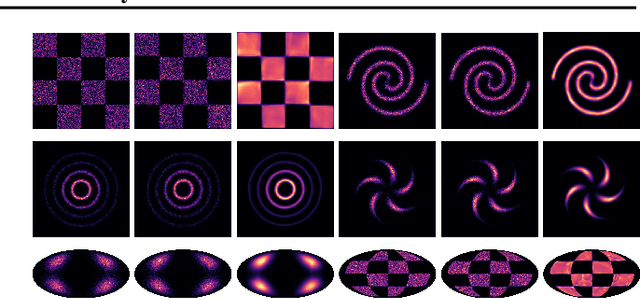
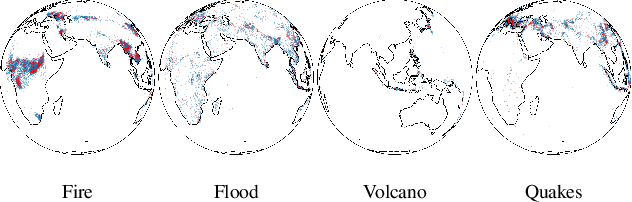
Continuous Normalizing Flows (CNFs) are a class of generative models that transform a prior distribution to a model distribution by solving an ordinary differential equation (ODE). We propose to train CNFs on manifolds by minimizing probability path divergence (PPD), a novel family of divergences between the probability density path generated by the CNF and a target probability density path. PPD is formulated using a logarithmic mass conservation formula which is a linear first order partial differential equation relating the log target probabilities and the CNF's defining vector field. PPD has several key benefits over existing methods: it sidesteps the need to solve an ODE per iteration, readily applies to manifold data, scales to high dimensions, and is compatible with a large family of target paths interpolating pure noise and data in finite time. Theoretically, PPD is shown to bound classical probability divergences. Empirically, we show that CNFs learned by minimizing PPD achieve state-of-the-art results in likelihoods and sample quality on existing low-dimensional manifold benchmarks, and is the first example of a generative model to scale to moderately high dimensional manifolds.

Meta Optimal Transport

We study the use of amortized optimization to predict optimal transport (OT) maps from the input measures, which we call Meta OT. This helps repeatedly solve similar OT problems between different measures by leveraging the knowledge and information present from past problems to rapidly predict and solve new problems. Otherwise, standard methods ignore the knowledge of the past solutions and suboptimally re-solve each problem from scratch. Meta OT models surpass the standard convergence rates of log-Sinkhorn solvers in the discrete setting and convex potentials in the continuous setting. We improve the computational time of standard OT solvers by multiple orders of magnitude in discrete and continuous transport settings between images, spherical data, and color palettes. Our source code is available at http://github.com/facebookresearch/meta-ot.

Cross-Domain Imitation Learning via Optimal Transport

Cross-domain imitation learning studies how to leverage expert demonstrations of one agent to train an imitation agent with a different embodiment or morphology. Comparing trajectories and stationary distributions between the expert and imitation agents is challenging because they live on different systems that may not even have the same dimensionality. We propose Gromov-Wasserstein Imitation Learning (GWIL), a method for cross-domain imitation that uses the Gromov-Wasserstein distance to align and compare states between the different spaces of the agents. Our theory formally characterizes the scenarios where GWIL preserves optimality, revealing its possibilities and limitations. We demonstrate the effectiveness of GWIL in non-trivial continuous control domains ranging from simple rigid transformation of the expert domain to arbitrary transformation of the state-action space.

Riemannian Convex Potential Maps

Modeling distributions on Riemannian manifolds is a crucial component in understanding non-Euclidean data that arises, e.g., in physics and geology. The budding approaches in this space are limited by representational and computational tradeoffs. We propose and study a class of flows that uses convex potentials from Riemannian optimal transport. These are universal and can model distributions on any compact Riemannian manifold without requiring domain knowledge of the manifold to be integrated into the architecture. We demonstrate that these flows can model standard distributions on spheres, and tori, on synthetic and geological data. Our source code is freely available online at http://github.com/facebookresearch/rcpm

Sliced Multi-Marginal Optimal Transport

We study multi-marginal optimal transport, a generalization of optimal transport that allows us to define discrepancies between multiple measures. It provides a framework to solve multi-task learning problems and to perform barycentric averaging. However, multi-marginal distances between multiple measures are typically challenging to compute because they require estimating a transport plan with $N^P$ variables. In this paper, we address this issue in the following way: 1) we efficiently solve the one-dimensional multi-marginal Monge-Wasserstein problem for a classical cost function in closed form, and 2) we propose a higher-dimensional multi-marginal discrepancy via slicing and study its generalized metric properties. We show that computing the sliced multi-marginal discrepancy is massively scalable for a large number of probability measures with support as large as $10^7$ samples. Our approach can be applied to solving problems such as barycentric averaging, multi-task density estimation and multi-task reinforcement learning.

Healing Products of Gaussian Processes

Gaussian processes (GPs) are nonparametric Bayesian models that have been applied to regression and classification problems. One of the approaches to alleviate their cubic training cost is the use of local GP experts trained on subsets of the data. In particular, product-of-expert models combine the predictive distributions of local experts through a tractable product operation. While these expert models allow for massively distributed computation, their predictions typically suffer from erratic behaviour of the mean or uncalibrated uncertainty quantification. By calibrating predictions via a tempered softmax weighting, we provide a solution to these problems for multiple product-of-expert models, including the generalised product of experts and the robust Bayesian committee machine. Furthermore, we leverage the optimal transport literature and propose a new product-of-expert model that combines predictions of local experts by computing their Wasserstein barycenter, which can be applied to both regression and classification.

Correlated Bandits for Dynamic Pricing via the ARC algorithm

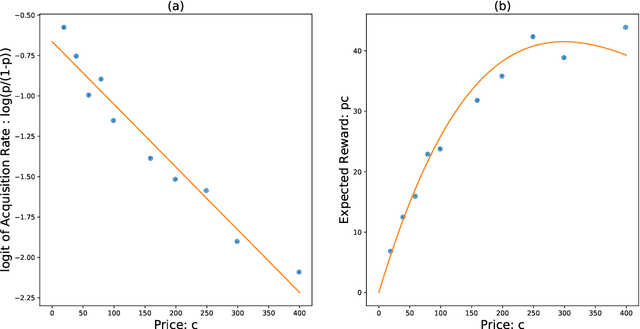
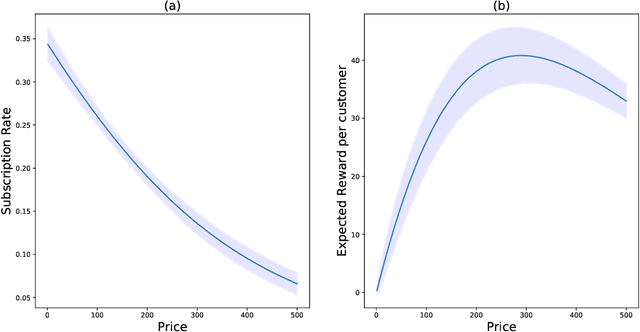
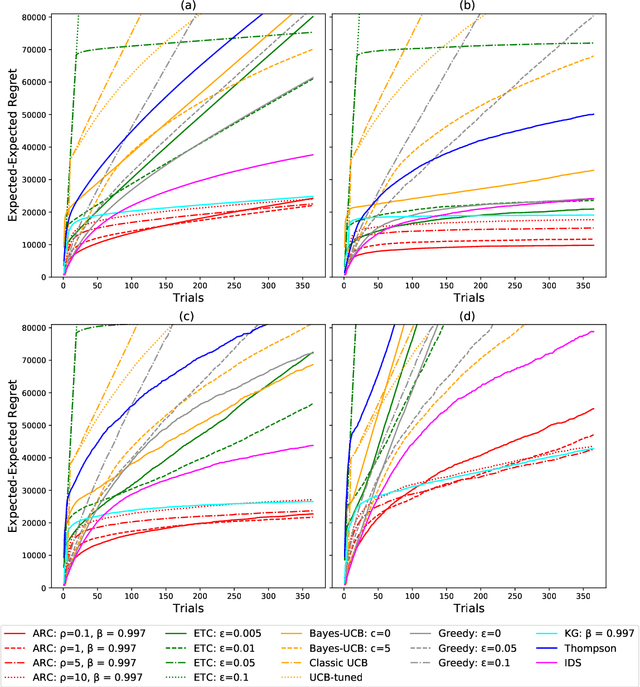
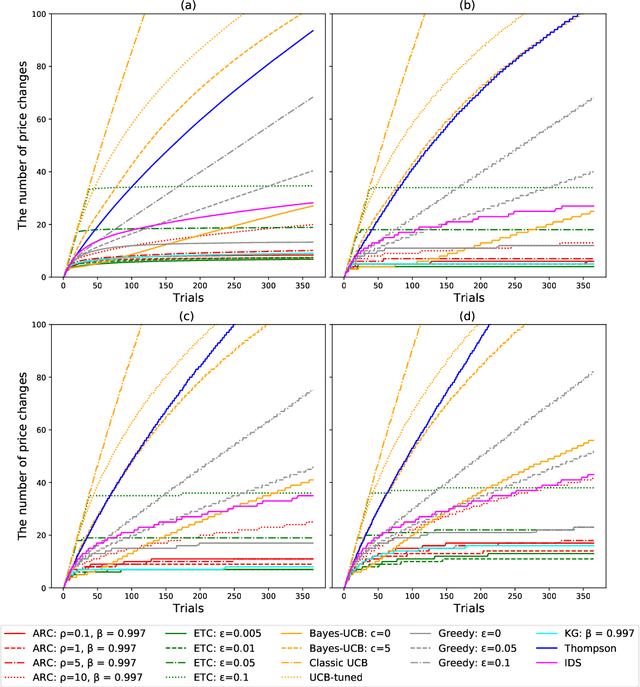
The Asymptotic Randomised Control (ARC) algorithm provides a rigorous approximation to the optimal strategy for a wide class of Bayesian bandits, while retaining reasonable computational complexity. In particular, it allows a decision maker to observe signals in addition to their rewards, to incorporate correlations between the outcomes of different choices, and to have nontrivial dynamics for their estimates. The algorithm is guaranteed to asymptotically optimise the expected discounted payoff, with error depending on the initial uncertainty of the bandit. In this paper, we consider a batched bandit problem where observations arrive from a generalised linear model; we extend the ARC algorithm to this setting. We apply this to a classic dynamic pricing problem based on a Bayesian hierarchical model and demonstrate that the ARC algorithm outperforms alternative approaches.

Estimating Barycenters of Measures in High Dimensions

Barycentric averaging is a principled way of summarizing populations of measures. Existing algorithms for estimating barycenters typically parametrize them as weighted sums of Diracs and optimize their weights and/or locations. However, these approaches do not scale to high-dimensional settings due to the curse of dimensionality. In this paper, we propose a scalable and general algorithm for estimating barycenters of measures in high dimensions. The key idea is to turn the optimization over measures into an optimization over generative models, introducing inductive biases that allow the method to scale while still accurately estimating barycenters. We prove local convergence under mild assumptions on the discrepancy showing that the approach is well-posed. We demonstrate that our method is fast, achieves good performance on low-dimensional problems, and scales to high-dimensional settings. In particular, our approach is the first to be used to estimate barycenters in thousands of dimensions.