$ε$-Policy Gradient for Online Pricing

Combining model-based and model-free reinforcement learning approaches, this paper proposes and analyzes an $\epsilon$-policy gradient algorithm for the online pricing learning task. The algorithm extends $\epsilon$-greedy algorithm by replacing greedy exploitation with gradient descent step and facilitates learning via model inference. We optimize the regret of the proposed algorithm by quantifying the exploration cost in terms of the exploration probability $\epsilon$ and the exploitation cost in terms of the gradient descent optimization and gradient estimation errors. The algorithm achieves an expected regret of order $\mathcal{O}(\sqrt{T})$ (up to a logarithmic factor) over $T$ trials.

Insurance pricing on price comparison websites via reinforcement learning

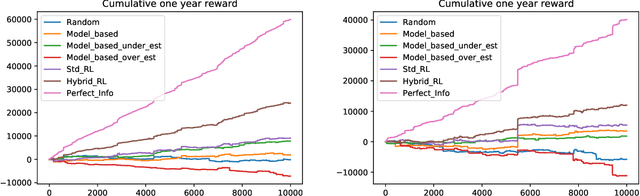
The emergence of price comparison websites (PCWs) has presented insurers with unique challenges in formulating effective pricing strategies. Operating on PCWs requires insurers to strike a delicate balance between competitive premiums and profitability, amidst obstacles such as low historical conversion rates, limited visibility of competitors' actions, and a dynamic market environment. In addition to this, the capital intensive nature of the business means pricing below the risk levels of customers can result in solvency issues for the insurer. To address these challenges, this paper introduces reinforcement learning (RL) framework that learns the optimal pricing policy by integrating model-based and model-free methods. The model-based component is used to train agents in an offline setting, avoiding cold-start issues, while model-free algorithms are then employed in a contextual bandit (CB) manner to dynamically update the pricing policy to maximise the expected revenue. This facilitates quick adaptation to evolving market dynamics and enhances algorithm efficiency and decision interpretability. The paper also highlights the importance of evaluating pricing policies using an offline dataset in a consistent fashion and demonstrates the superiority of the proposed methodology over existing off-the-shelf RL/CB approaches. We validate our methodology using synthetic data, generated to reflect private commercially available data within real-world insurers, and compare against 6 other benchmark approaches. Our hybrid agent outperforms these benchmarks in terms of sample efficiency and cumulative reward with the exception of an agent that has access to perfect market information which would not be available in a real-world set-up.

Optimal scheduling of entropy regulariser for continuous-time linear-quadratic reinforcement learning

This work uses the entropy-regularised relaxed stochastic control perspective as a principled framework for designing reinforcement learning (RL) algorithms. Herein agent interacts with the environment by generating noisy controls distributed according to the optimal relaxed policy. The noisy policies, on the one hand, explore the space and hence facilitate learning but, on the other hand, introduce bias by assigning a positive probability to non-optimal actions. This exploration-exploitation trade-off is determined by the strength of entropy regularisation. We study algorithms resulting from two entropy regularisation formulations: the exploratory control approach, where entropy is added to the cost objective, and the proximal policy update approach, where entropy penalises the divergence of policies between two consecutive episodes. We analyse the finite horizon continuous-time linear-quadratic (LQ) RL problem for which both algorithms yield a Gaussian relaxed policy. We quantify the precise difference between the value functions of a Gaussian policy and its noisy evaluation and show that the execution noise must be independent across time. By tuning the frequency of sampling from relaxed policies and the parameter governing the strength of entropy regularisation, we prove that the regret, for both learning algorithms, is of the order $\mathcal{O}(\sqrt{N}) $ (up to a logarithmic factor) over $N$ episodes, matching the best known result from the literature.

Exploration-exploitation trade-off for continuous-time episodic reinforcement learning with linear-convex models

We develop a probabilistic framework for analysing model-based reinforcement learning in the episodic setting. We then apply it to study finite-time horizon stochastic control problems with linear dynamics but unknown coefficients and convex, but possibly irregular, objective function. Using probabilistic representations, we study regularity of the associated cost functions and establish precise estimates for the performance gap between applying optimal feedback control derived from estimated and true model parameters. We identify conditions under which this performance gap is quadratic, improving the linear performance gap in recent work [X. Guo, A. Hu, and Y. Zhang, arXiv preprint, arXiv:2104.09311, (2021)], which matches the results obtained for stochastic linear-quadratic problems. Next, we propose a phase-based learning algorithm for which we show how to optimise exploration-exploitation trade-off and achieve sublinear regrets in high probability and expectation. When assumptions needed for the quadratic performance gap hold, the algorithm achieves an order $\mathcal{O}(\sqrt{N} \ln N)$ high probability regret, in the general case, and an order $\mathcal{O}((\ln N)^2)$ expected regret, in self-exploration case, over $N$ episodes, matching the best possible results from the literature. The analysis requires novel concentration inequalities for correlated continuous-time observations, which we derive.

Correlated Bandits for Dynamic Pricing via the ARC algorithm

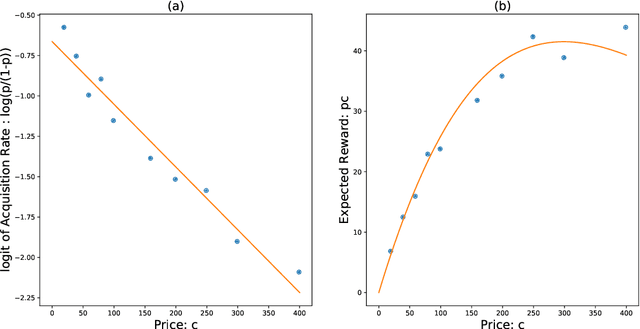
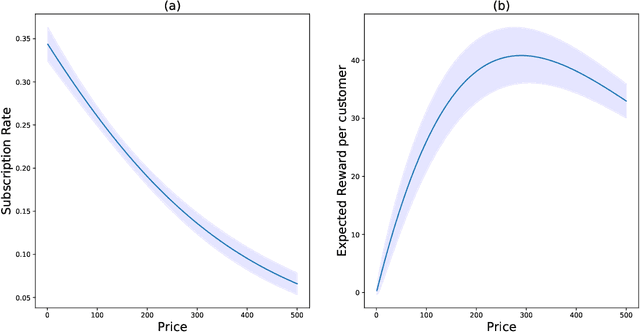
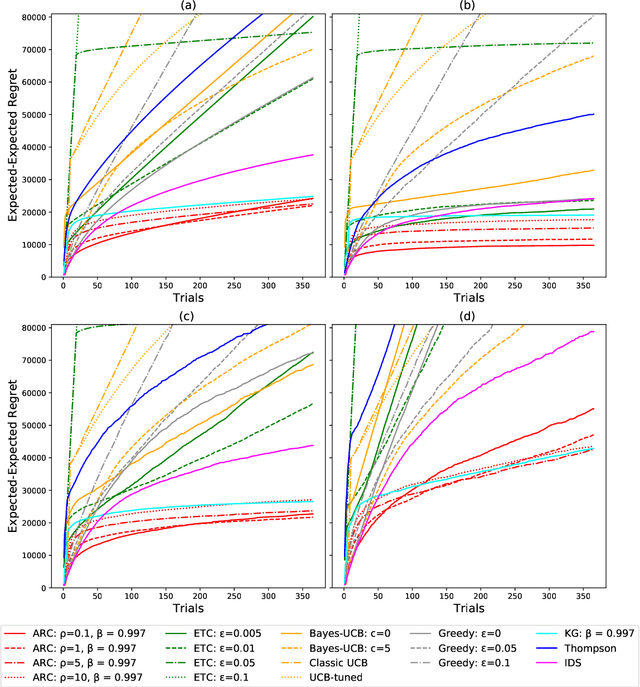
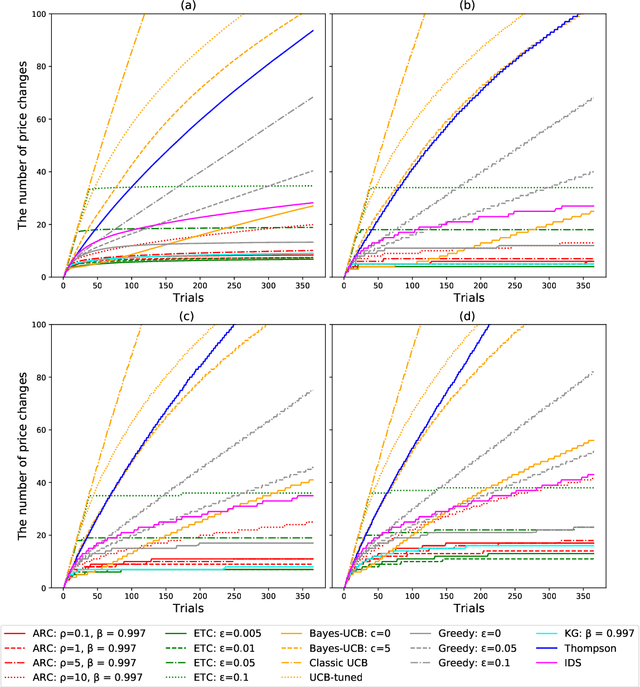
The Asymptotic Randomised Control (ARC) algorithm provides a rigorous approximation to the optimal strategy for a wide class of Bayesian bandits, while retaining reasonable computational complexity. In particular, it allows a decision maker to observe signals in addition to their rewards, to incorporate correlations between the outcomes of different choices, and to have nontrivial dynamics for their estimates. The algorithm is guaranteed to asymptotically optimise the expected discounted payoff, with error depending on the initial uncertainty of the bandit. In this paper, we consider a batched bandit problem where observations arrive from a generalised linear model; we extend the ARC algorithm to this setting. We apply this to a classic dynamic pricing problem based on a Bayesian hierarchical model and demonstrate that the ARC algorithm outperforms alternative approaches.

Asymptotic Randomised Control with applications to bandits

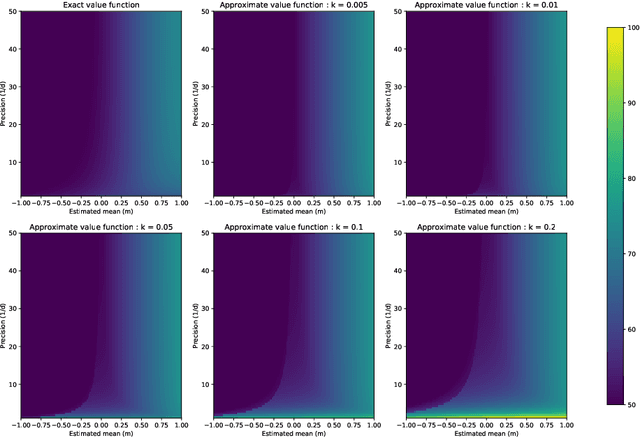
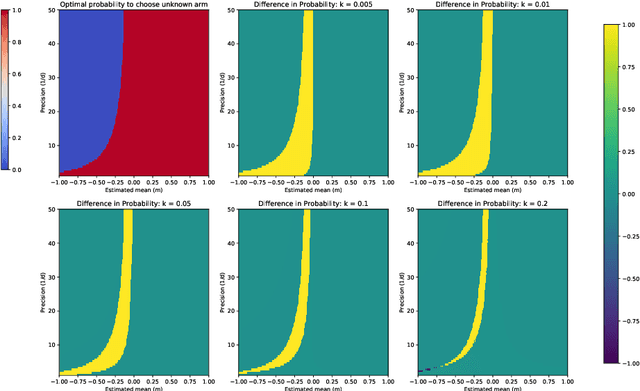
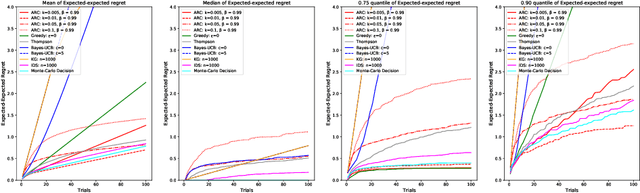
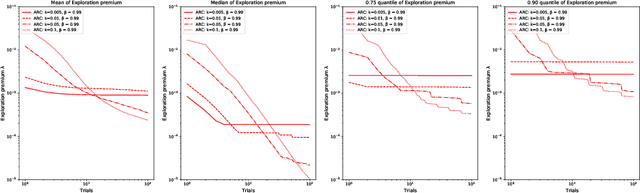
We consider a general multi-armed bandit problem with correlated (and simple contextual and restless) elements, as a relaxed control problem. By introducing an entropy premium, we obtain a smooth asymptotic approximation to the value function. This yields a novel semi-index approximation of the optimal decision process, obtained numerically by solving a fixed point problem, which can be interpreted as explicitly balancing an exploration-exploitation trade-off. Performance of the resulting Asymptotic Randomised Control (ARC) algorithm compares favourably with other approaches to correlated multi-armed bandits.