Correlated Bandits for Dynamic Pricing via the ARC algorithm
Paper and Code
Feb 08, 2021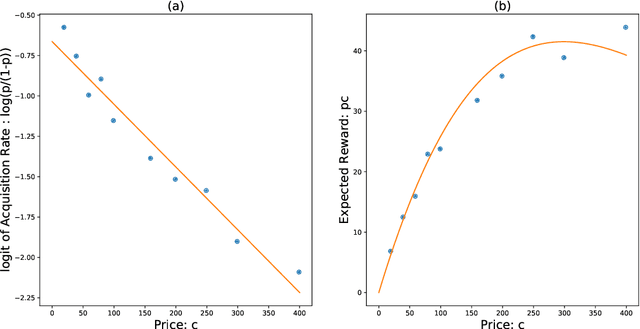
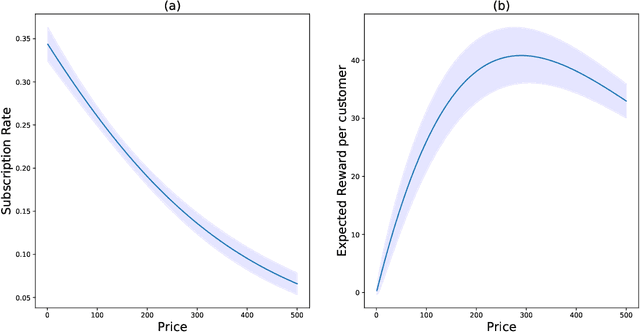
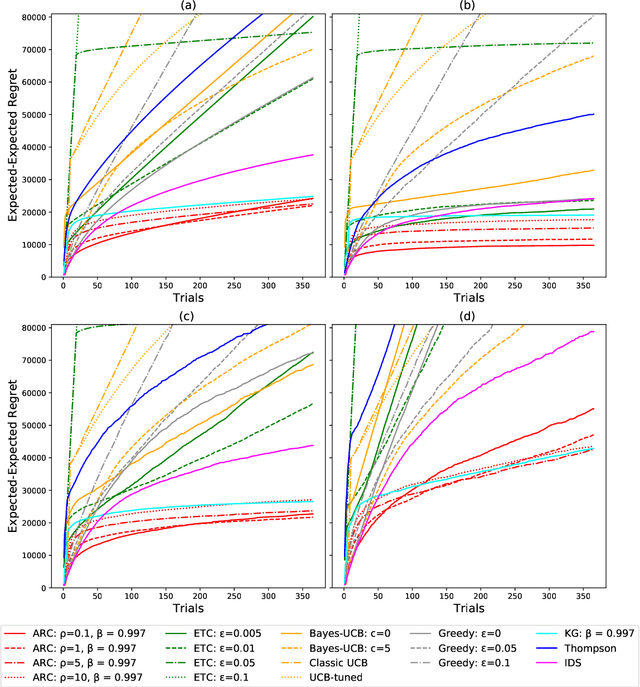
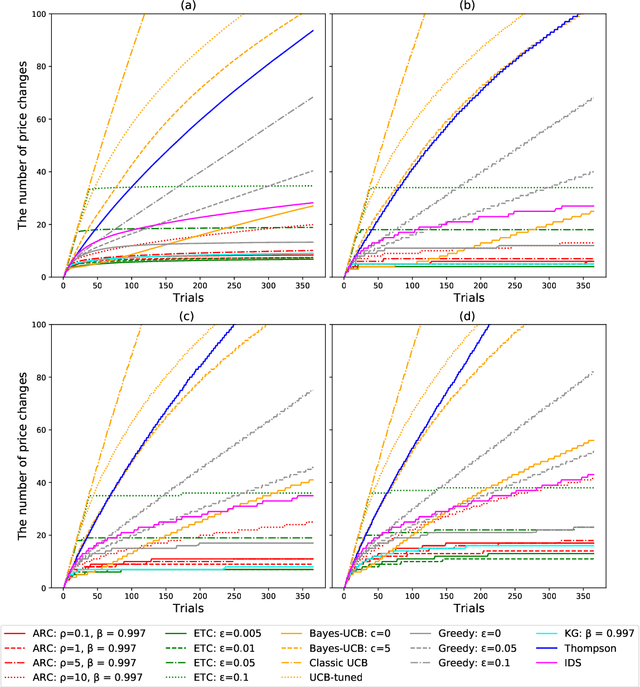
The Asymptotic Randomised Control (ARC) algorithm provides a rigorous approximation to the optimal strategy for a wide class of Bayesian bandits, while retaining reasonable computational complexity. In particular, it allows a decision maker to observe signals in addition to their rewards, to incorporate correlations between the outcomes of different choices, and to have nontrivial dynamics for their estimates. The algorithm is guaranteed to asymptotically optimise the expected discounted payoff, with error depending on the initial uncertainty of the bandit. In this paper, we consider a batched bandit problem where observations arrive from a generalised linear model; we extend the ARC algorithm to this setting. We apply this to a classic dynamic pricing problem based on a Bayesian hierarchical model and demonstrate that the ARC algorithm outperforms alternative approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge