Unsupervised Imaging Inverse Problems with Diffusion Distribution Matching

This work addresses image restoration tasks through the lens of inverse problems using unpaired datasets. In contrast to traditional approaches -- which typically assume full knowledge of the forward model or access to paired degraded and ground-truth images -- the proposed method operates under minimal assumptions and relies only on small, unpaired datasets. This makes it particularly well-suited for real-world scenarios, where the forward model is often unknown or misspecified, and collecting paired data is costly or infeasible. The method leverages conditional flow matching to model the distribution of degraded observations, while simultaneously learning the forward model via a distribution-matching loss that arises naturally from the framework. Empirically, it outperforms both single-image blind and unsupervised approaches on deblurring and non-uniform point spread function (PSF) calibration tasks. It also matches state-of-the-art performance on blind super-resolution. We also showcase the effectiveness of our method with a proof of concept for lens calibration: a real-world application traditionally requiring time-consuming experiments and specialized equipment. In contrast, our approach achieves this with minimal data acquisition effort.

Learning Theory for Kernel Bilevel Optimization

Bilevel optimization has emerged as a technique for addressing a wide range of machine learning problems that involve an outer objective implicitly determined by the minimizer of an inner problem. In this paper, we investigate the generalization properties for kernel bilevel optimization problems where the inner objective is optimized over a Reproducing Kernel Hilbert Space. This setting enables rich function approximation while providing a foundation for rigorous theoretical analysis. In this context, we establish novel generalization error bounds for the bilevel problem under finite-sample approximation. Our approach adopts a functional perspective, inspired by (Petrulionyte et al., 2024), and leverages tools from empirical process theory and maximal inequalities for degenerate $U$-processes to derive uniform error bounds. These generalization error estimates allow to characterize the statistical accuracy of gradient-based methods applied to the empirical discretization of the bilevel problem.

EquiTabPFN: A Target-Permutation Equivariant Prior Fitted Networks

Recent foundational models for tabular data, such as TabPFN, have demonstrated remarkable effectiveness in adapting to new tasks through in-context learning. However, these models overlook a crucial equivariance property: the arbitrary ordering of target dimensions should not influence model predictions. In this study, we identify this oversight as a source of incompressible error, termed the equivariance gap, which introduces instability in predictions. To mitigate these issues, we propose a novel model designed to preserve equivariance across output dimensions. Our experimental results indicate that our proposed model not only addresses these pitfalls effectively but also achieves competitive benchmark performance.

LUDVIG: Learning-free Uplifting of 2D Visual features to Gaussian Splatting scenes

We address the task of uplifting visual features or semantic masks from 2D vision models to 3D scenes represented by Gaussian Splatting. Whereas common approaches rely on iterative optimization-based procedures, we show that a simple yet effective aggregation technique yields excellent results. Applied to semantic masks from Segment Anything (SAM), our uplifting approach leads to segmentation quality comparable to the state of the art. We then extend this method to generic DINOv2 features, integrating 3D scene geometry through graph diffusion, and achieve competitive segmentation results despite DINOv2 not being trained on millions of annotated masks like SAM.

Functional Bilevel Optimization for Machine Learning

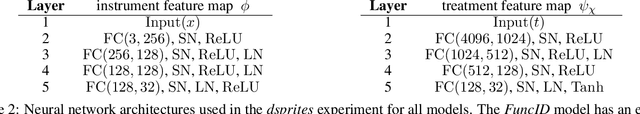
In this paper, we introduce a new functional point of view on bilevel optimization problems for machine learning, where the inner objective is minimized over a function space. These types of problems are most often solved by using methods developed in the parametric setting, where the inner objective is strongly convex with respect to the parameters of the prediction function. The functional point of view does not rely on this assumption and notably allows using over-parameterized neural networks as the inner prediction function. We propose scalable and efficient algorithms for the functional bilevel optimization problem and illustrate the benefits of our approach on instrumental regression and reinforcement learning tasks, which admit natural functional bilevel structures.

MLXP: A framework for conducting replicable Machine Learning eXperiments in Python

Replicability in machine learning (ML) research is increasingly concerning due to the utilization of complex non-deterministic algorithms and the dependence on numerous hyper-parameter choices, such as model architecture and training datasets. Ensuring reproducible and replicable results is crucial for advancing the field, yet often requires significant technical effort to conduct systematic and well-organized experiments that yield robust conclusions. Several tools have been developed to facilitate experiment management and enhance reproducibility; however, they often introduce complexity that hinders adoption within the research community, despite being well-handled in industrial settings. To address the challenge of low adoption, we propose MLXP, an open-source, simple, and lightweight experiment management tool based on Python, available at https://github.com/inria-thoth/mlxp . MLXP streamlines the experimental process with minimal practitioner overhead while ensuring a high level of reproducibility.

On Good Practices for Task-Specific Distillation of Large Pretrained Models

Large pretrained visual models exhibit remarkable generalization across diverse recognition tasks. Yet, real-world applications often demand compact models tailored to specific problems. Variants of knowledge distillation have been devised for such a purpose, enabling task-specific compact models (the students) to learn from a generic large pretrained one (the teacher). In this paper, we show that the excellent robustness and versatility of recent pretrained models challenge common practices established in the literature, calling for a new set of optimal guidelines for task-specific distillation. To address the lack of samples in downstream tasks, we also show that a variant of Mixup based on stable diffusion complements standard data augmentation. This strategy eliminates the need for engineered text prompts and improves distillation of generic models into streamlined specialized networks.

SLACK: Stable Learning of Augmentations with Cold-start and KL regularization

Data augmentation is known to improve the generalization capabilities of neural networks, provided that the set of transformations is chosen with care, a selection often performed manually. Automatic data augmentation aims at automating this process. However, most recent approaches still rely on some prior information; they start from a small pool of manually-selected default transformations that are either used to pretrain the network or forced to be part of the policy learned by the automatic data augmentation algorithm. In this paper, we propose to directly learn the augmentation policy without leveraging such prior knowledge. The resulting bilevel optimization problem becomes more challenging due to the larger search space and the inherent instability of bilevel optimization algorithms. To mitigate these issues (i) we follow a successive cold-start strategy with a Kullback-Leibler regularization, and (ii) we parameterize magnitudes as continuous distributions. Our approach leads to competitive results on standard benchmarks despite a more challenging setting, and generalizes beyond natural images.

Rethinking Gauss-Newton for learning over-parameterized models

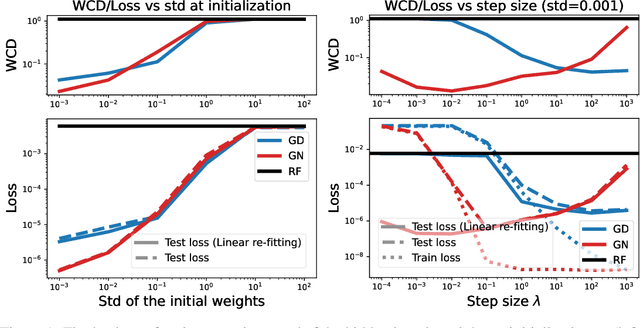
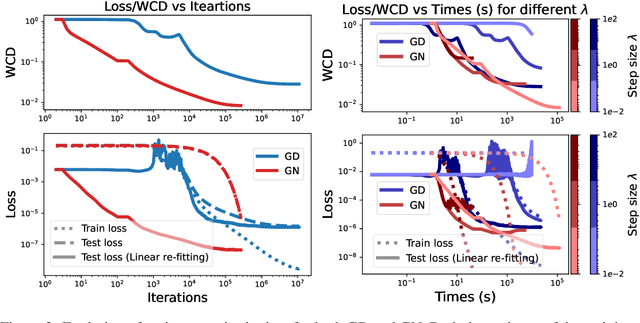
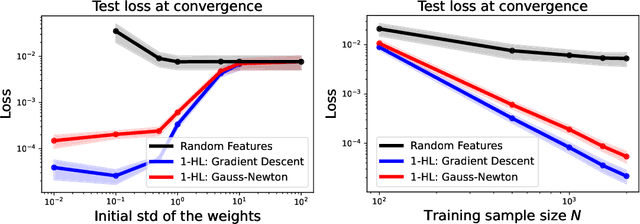
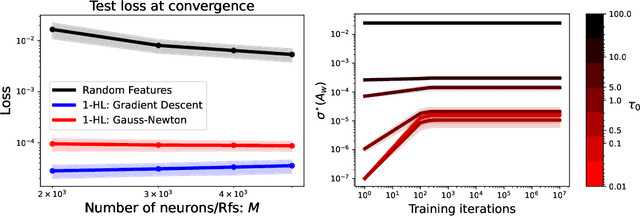
Compared to gradient descent, Gauss-Newton's method (GN) and variants are known to converge faster to local optima at the expense of a higher computational cost per iteration. Still, GN is not widely used for optimizing deep neural networks despite a constant effort to reduce their higher computational cost. In this work, we propose to take a step back and re-think the properties of GN in light of recent advances in the dynamics of gradient flows of over-parameterized models and the implicit bias they induce. We first prove a fast global convergence result for the continuous-time limit of the generalized GN in the over-parameterized regime. We then show empirically that GN exhibits both a kernel regime where it generalizes as well as gradient flows, and a feature learning regime where GN induces an implicit bias for selecting global solutions that systematically under-performs those found by a gradient flow. Importantly, we observed this phenomenon even with enough computational budget to perform exact GN steps over the total training objective. This study suggests the need to go beyond improving the computational cost of GN for over-parametrized models towards designing new methods that can trade off optimization speed and the quality of their implicit bias.

Maximum Likelihood Learning of Energy-Based Models for Simulation-Based Inference

We introduce two synthetic likelihood methods for Simulation-Based Inference (SBI), to conduct either amortized or targeted inference from experimental observations when a high-fidelity simulator is available. Both methods learn a conditional energy-based model (EBM) of the likelihood using synthetic data generated by the simulator, conditioned on parameters drawn from a proposal distribution. The learned likelihood can then be combined with any prior to obtain a posterior estimate, from which samples can be drawn using MCMC. Our methods uniquely combine a flexible Energy-Based Model and the minimization of a KL loss: this is in contrast to other synthetic likelihood methods, which either rely on normalizing flows, or minimize score-based objectives; choices that come with known pitfalls. Our first method, Amortized Unnormalized Neural Likelihood Estimation (AUNLE), introduces a tilting trick during training that allows to significantly lower the computational cost of inference by enabling the use of efficient MCMC techniques. Our second method, Sequential UNLE (SUNLE), employs a robust doubly intractable approach in order to re-use simulation data and improve posterior accuracy on a specific dataset. We demonstrate the properties of both methods on a range of synthetic datasets, and apply them to a neuroscience model of the pyloric network in the crab Cancer Borealis, matching the performance of other synthetic likelihood methods at a fraction of the simulation budget.