Non-Stationary Functional Bilevel Optimization

Functional bilevel optimization (FBO) provides a powerful framework for hierarchical learning in function spaces, yet current methods are limited to static offline settings and perform suboptimally in online, non-stationary scenarios. We propose SmoothFBO, the first algorithm for non-stationary FBO with both theoretical guarantees and practical scalability. SmoothFBO introduces a time-smoothed stochastic hypergradient estimator that reduces variance through a window parameter, enabling stable outer-loop updates with sublinear regret. Importantly, the classical parametric bilevel case is a special reduction of our framework, making SmoothFBO a natural extension to online, non-stationary settings. Empirically, SmoothFBO consistently outperforms existing FBO methods in non-stationary hyperparameter optimization and model-based reinforcement learning, demonstrating its practical effectiveness. Together, these results establish SmoothFBO as a general, theoretically grounded, and practically viable foundation for bilevel optimization in online, non-stationary scenarios.

Functional Bilevel Optimization for Machine Learning

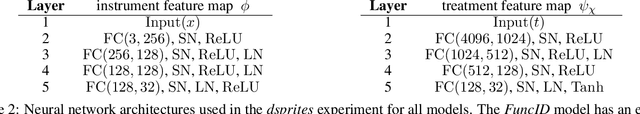
In this paper, we introduce a new functional point of view on bilevel optimization problems for machine learning, where the inner objective is minimized over a function space. These types of problems are most often solved by using methods developed in the parametric setting, where the inner objective is strongly convex with respect to the parameters of the prediction function. The functional point of view does not rely on this assumption and notably allows using over-parameterized neural networks as the inner prediction function. We propose scalable and efficient algorithms for the functional bilevel optimization problem and illustrate the benefits of our approach on instrumental regression and reinforcement learning tasks, which admit natural functional bilevel structures.