Rethinking Gauss-Newton for learning over-parameterized models

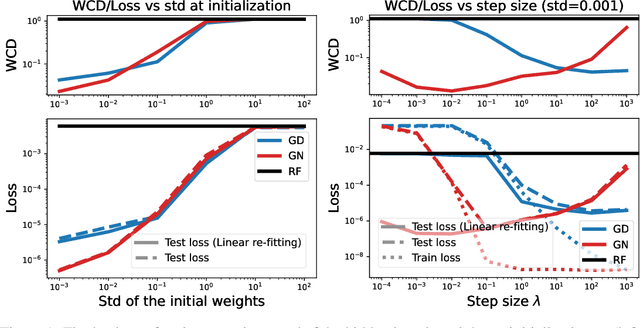
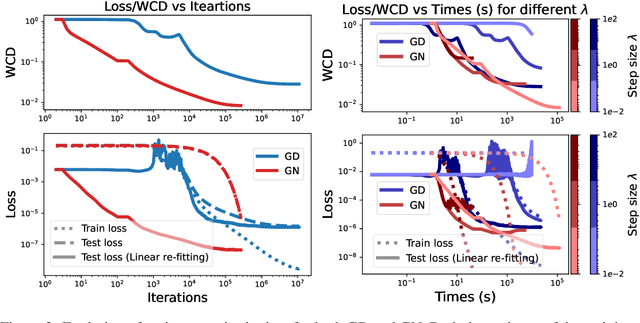
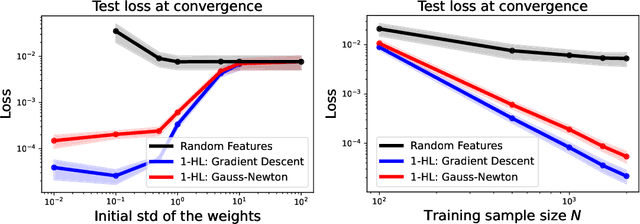
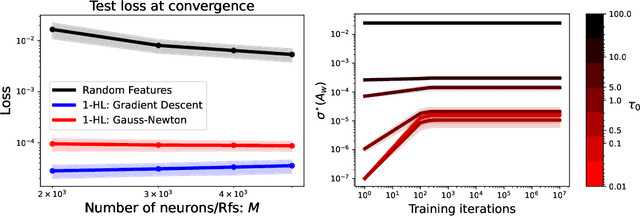
Compared to gradient descent, Gauss-Newton's method (GN) and variants are known to converge faster to local optima at the expense of a higher computational cost per iteration. Still, GN is not widely used for optimizing deep neural networks despite a constant effort to reduce their higher computational cost. In this work, we propose to take a step back and re-think the properties of GN in light of recent advances in the dynamics of gradient flows of over-parameterized models and the implicit bias they induce. We first prove a fast global convergence result for the continuous-time limit of the generalized GN in the over-parameterized regime. We then show empirically that GN exhibits both a kernel regime where it generalizes as well as gradient flows, and a feature learning regime where GN induces an implicit bias for selecting global solutions that systematically under-performs those found by a gradient flow. Importantly, we observed this phenomenon even with enough computational budget to perform exact GN steps over the total training objective. This study suggests the need to go beyond improving the computational cost of GN for over-parametrized models towards designing new methods that can trade off optimization speed and the quality of their implicit bias.