Unsupervised Imaging Inverse Problems with Diffusion Distribution Matching

This work addresses image restoration tasks through the lens of inverse problems using unpaired datasets. In contrast to traditional approaches -- which typically assume full knowledge of the forward model or access to paired degraded and ground-truth images -- the proposed method operates under minimal assumptions and relies only on small, unpaired datasets. This makes it particularly well-suited for real-world scenarios, where the forward model is often unknown or misspecified, and collecting paired data is costly or infeasible. The method leverages conditional flow matching to model the distribution of degraded observations, while simultaneously learning the forward model via a distribution-matching loss that arises naturally from the framework. Empirically, it outperforms both single-image blind and unsupervised approaches on deblurring and non-uniform point spread function (PSF) calibration tasks. It also matches state-of-the-art performance on blind super-resolution. We also showcase the effectiveness of our method with a proof of concept for lens calibration: a real-world application traditionally requiring time-consuming experiments and specialized equipment. In contrast, our approach achieves this with minimal data acquisition effort.

Estimating Koopman operators with sketching to provably learn large scale dynamical systems

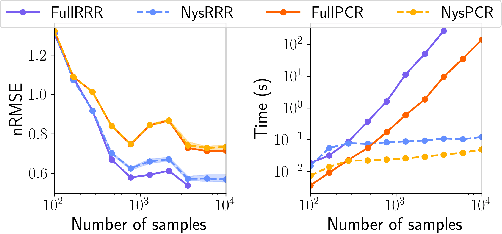
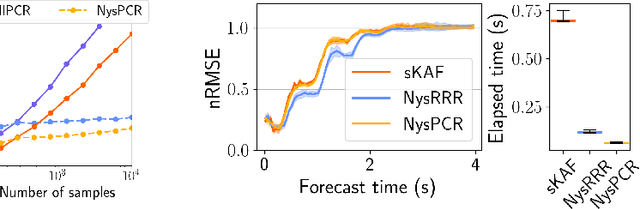
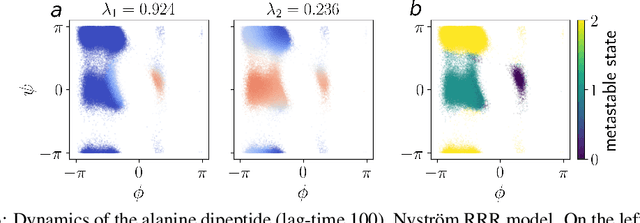
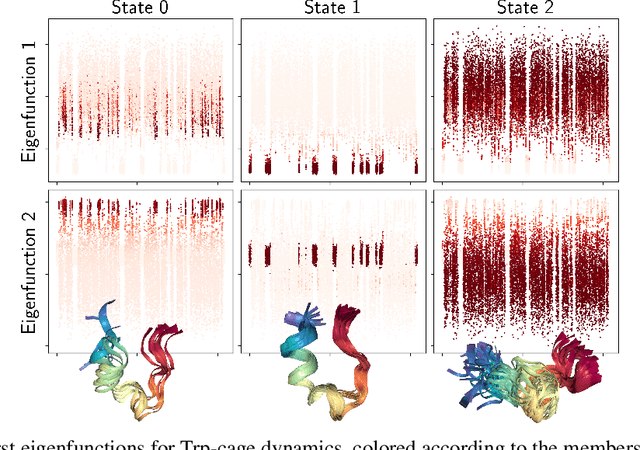
The theory of Koopman operators allows to deploy non-parametric machine learning algorithms to predict and analyze complex dynamical systems. Estimators such as principal component regression (PCR) or reduced rank regression (RRR) in kernel spaces can be shown to provably learn Koopman operators from finite empirical observations of the system's time evolution. Scaling these approaches to very long trajectories is a challenge and requires introducing suitable approximations to make computations feasible. In this paper, we boost the efficiency of different kernel-based Koopman operator estimators using random projections (sketching). We derive, implement and test the new "sketched" estimators with extensive experiments on synthetic and large-scale molecular dynamics datasets. Further, we establish non asymptotic error bounds giving a sharp characterization of the trade-offs between statistical learning rates and computational efficiency. Our empirical and theoretical analysis shows that the proposed estimators provide a sound and efficient way to learn large scale dynamical systems. In particular our experiments indicate that the proposed estimators retain the same accuracy of PCR or RRR, while being much faster.

K-Planes: Explicit Radiance Fields in Space, Time, and Appearance

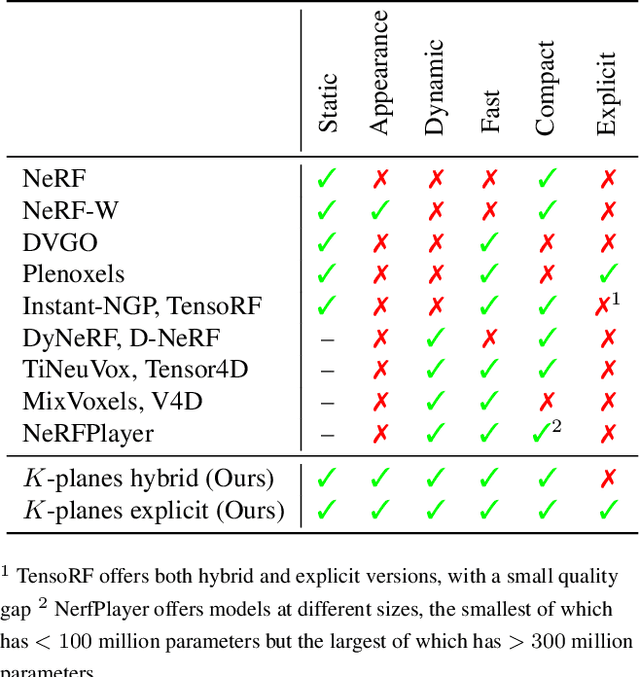
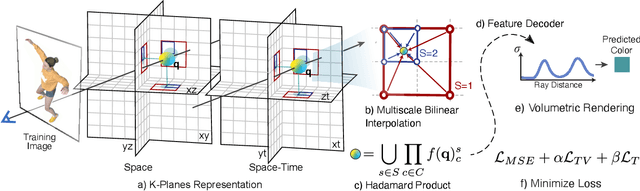
We introduce k-planes, a white-box model for radiance fields in arbitrary dimensions. Our model uses d choose 2 planes to represent a d-dimensional scene, providing a seamless way to go from static (d=3) to dynamic (d=4) scenes. This planar factorization makes adding dimension-specific priors easy, e.g. temporal smoothness and multi-resolution spatial structure, and induces a natural decomposition of static and dynamic components of a scene. We use a linear feature decoder with a learned color basis that yields similar performance as a nonlinear black-box MLP decoder. Across a range of synthetic and real, static and dynamic, fixed and varying appearance scenes, k-planes yields competitive and often state-of-the-art reconstruction fidelity with low memory usage, achieving 1000x compression over a full 4D grid, and fast optimization with a pure PyTorch implementation. For video results and code, please see sarafridov.github.io/K-Planes.

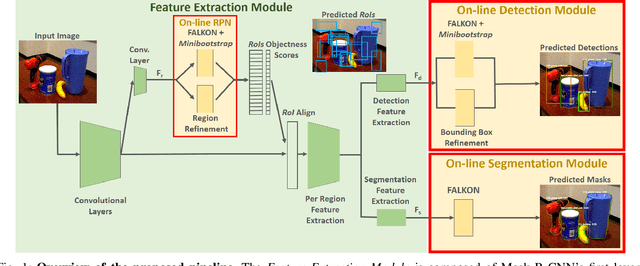
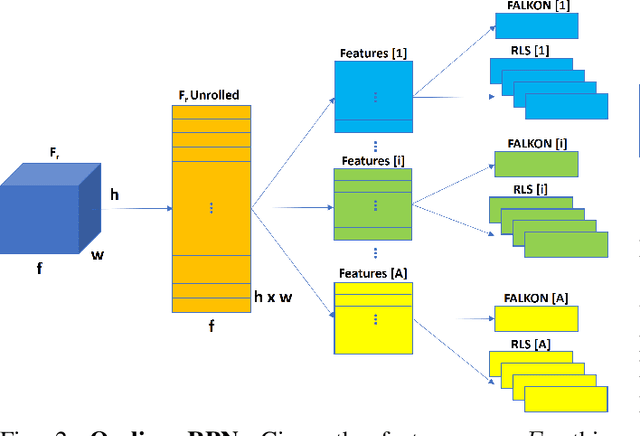
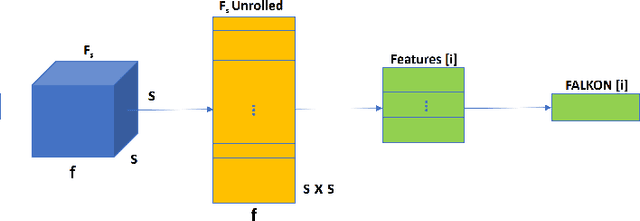
Learn Fast, Segment Well: Fast Object Segmentation Learning on the iCub Robot

The visual system of a robot has different requirements depending on the application: it may require high accuracy or reliability, be constrained by limited resources or need fast adaptation to dynamically changing environments. In this work, we focus on the instance segmentation task and provide a comprehensive study of different techniques that allow adapting an object segmentation model in presence of novel objects or different domains. We propose a pipeline for fast instance segmentation learning designed for robotic applications where data come in stream. It is based on an hybrid method leveraging on a pre-trained CNN for feature extraction and fast-to-train Kernel-based classifiers. We also propose a training protocol that allows to shorten the training time by performing feature extraction during the data acquisition. We benchmark the proposed pipeline on two robotics datasets and we deploy it on a real robot, i.e. the iCub humanoid. To this aim, we adapt our method to an incremental setting in which novel objects are learned on-line by the robot. The code to reproduce the experiments is publicly available on GitHub.

Physics Informed Shallow Machine Learning for Wind Speed Prediction

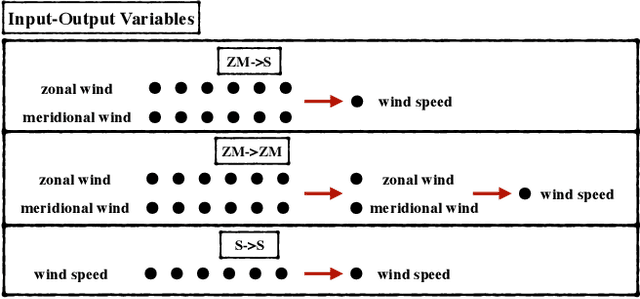
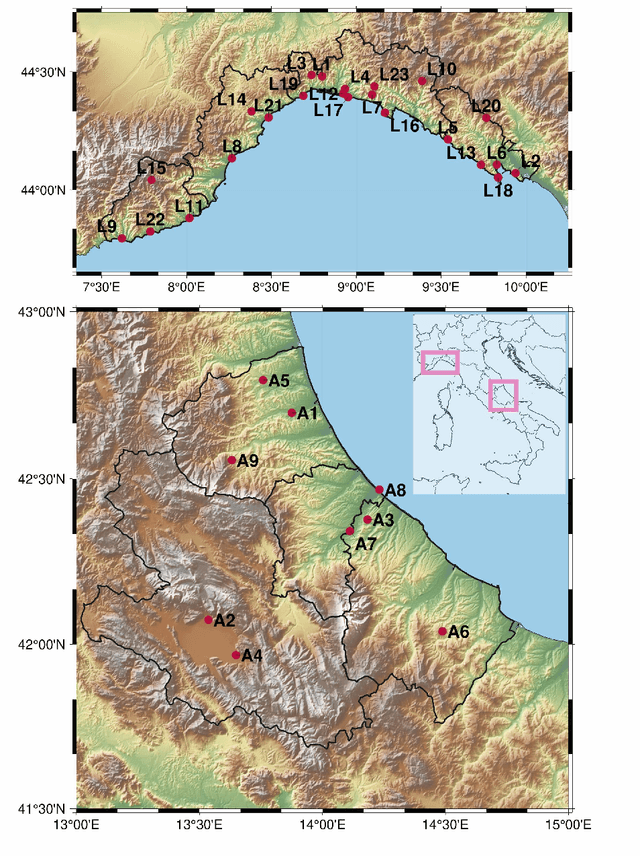
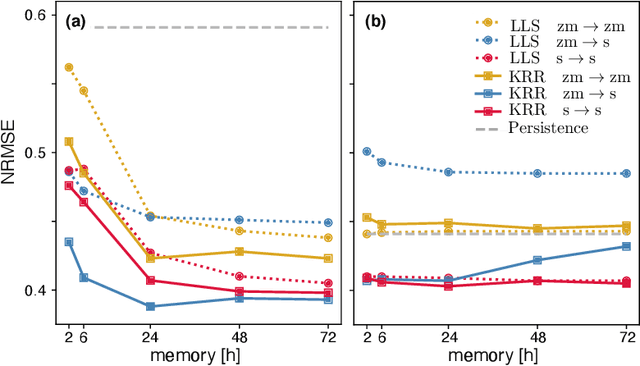
The ability to predict wind is crucial for both energy production and weather forecasting. Mechanistic models that form the basis of traditional forecasting perform poorly near the ground. In this paper, we take an alternative data-driven approach based on supervised learning. We analyze a massive dataset of wind measured from anemometers located at 10 m height in 32 locations in two central and north west regions of Italy (Abruzzo and Liguria). We train supervised learning algorithms using the past history of wind to predict its value at a future time (horizon). Using data from a single location and time horizon we compare systematically several algorithms where we vary the input/output variables, the memory of the input and the linear vs non-linear learning model. We then compare performance of the best algorithms across all locations and forecasting horizons. We find that the optimal design as well as its performance vary with the location. We demonstrate that the presence of a reproducible diurnal cycle provides a rationale to understand this variation. We conclude with a systematic comparison with state of the art algorithms and show that, when the model is accurately designed, shallow algorithms are competitive with more complex deep architectures.

Multiclass learning with margin: exponential rates with no bias-variance trade-off

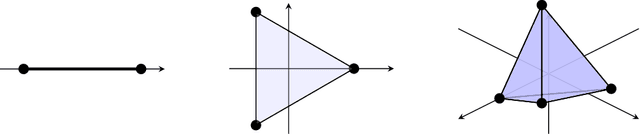
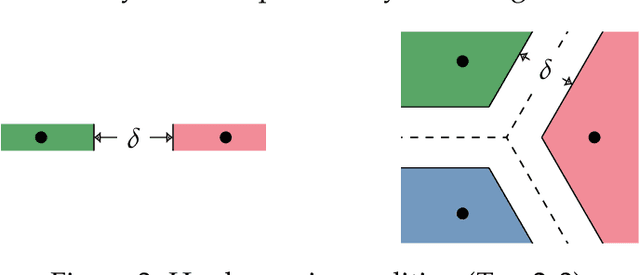
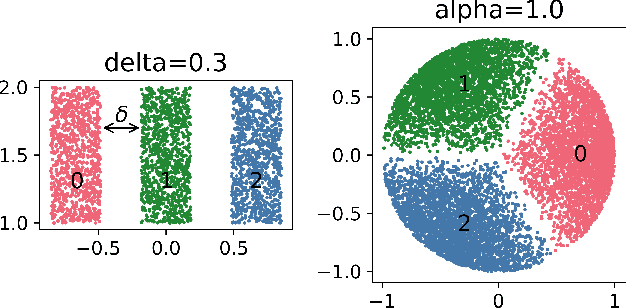
We study the behavior of error bounds for multiclass classification under suitable margin conditions. For a wide variety of methods we prove that the classification error under a hard-margin condition decreases exponentially fast without any bias-variance trade-off. Different convergence rates can be obtained in correspondence of different margin assumptions. With a self-contained and instructive analysis we are able to generalize known results from the binary to the multiclass setting.

Efficient Hyperparameter Tuning for Large Scale Kernel Ridge Regression

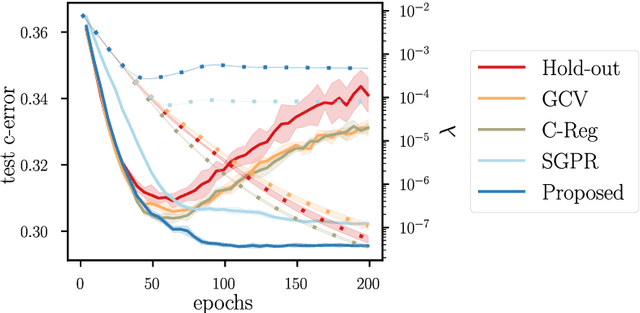
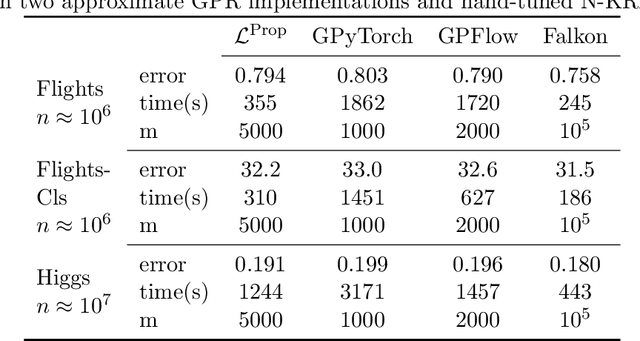
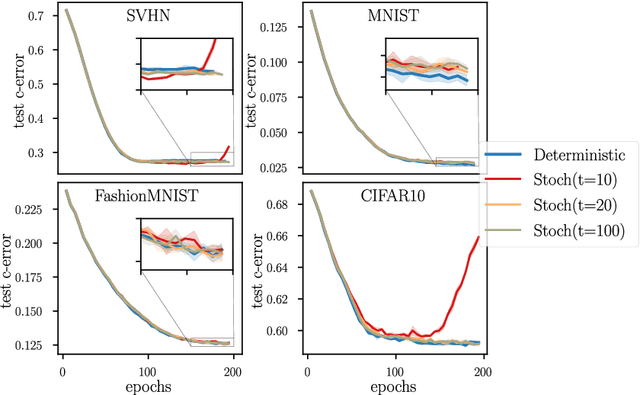
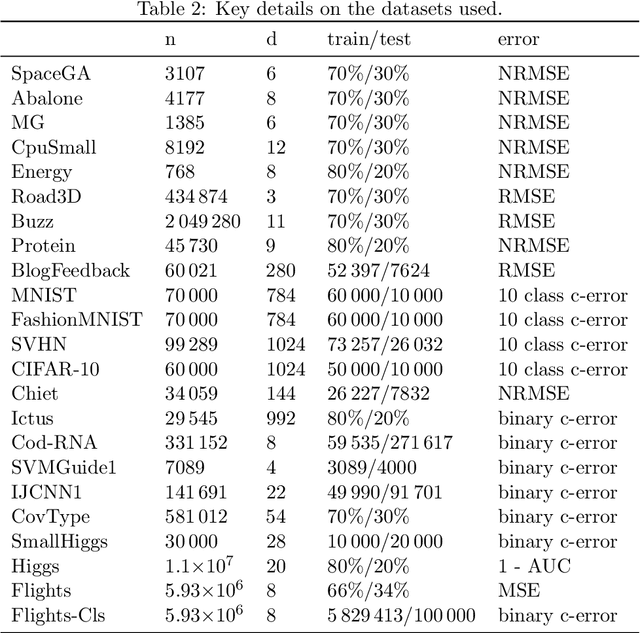
Kernel methods provide a principled approach to nonparametric learning. While their basic implementations scale poorly to large problems, recent advances showed that approximate solvers can efficiently handle massive datasets. A shortcoming of these solutions is that hyperparameter tuning is not taken care of, and left for the user to perform. Hyperparameters are crucial in practice and the lack of automated tuning greatly hinders efficiency and usability. In this paper, we work to fill in this gap focusing on kernel ridge regression based on the Nystr\"om approximation. After reviewing and contrasting a number of hyperparameter tuning strategies, we propose a complexity regularization criterion based on a data dependent penalty, and discuss its efficient optimization. Then, we proceed to a careful and extensive empirical evaluation highlighting strengths and weaknesses of the different tuning strategies. Our analysis shows the benefit of the proposed approach, that we hence incorporate in a library for large scale kernel methods to derive adaptively tuned solutions.

Kernel methods through the roof: handling billions of points efficiently

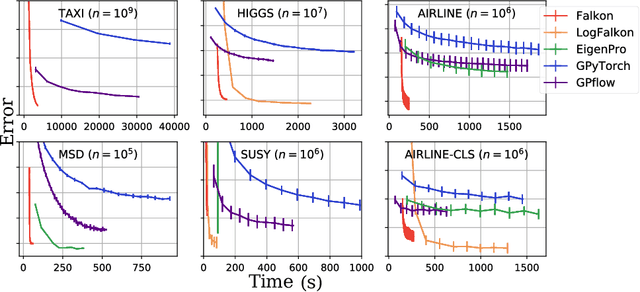
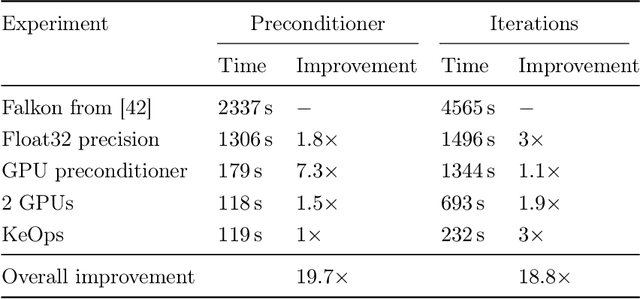
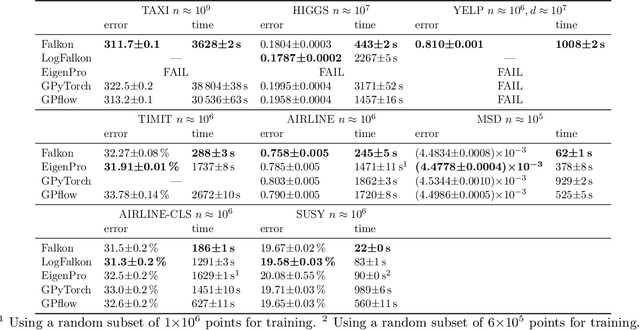
Kernel methods provide an elegant and principled approach to nonparametric learning, but so far could hardly be used in large scale problems, since na\"ive implementations scale poorly with data size. Recent advances have shown the benefits of a number of algorithmic ideas, for example combining optimization, numerical linear algebra and random projections. Here, we push these efforts further to develop and test a solver that takes full advantage of GPU hardware. Towards this end, we designed a preconditioned gradient solver for kernel methods exploiting both GPU acceleration and parallelization with multiple GPUs, implementing out-of-core variants of common linear algebra operations to guarantee optimal hardware utilization. Further, we optimize the numerical precision of different operations and maximize efficiency of matrix-vector multiplications. As a result we can experimentally show dramatic speedups on datasets with billions of points, while still guaranteeing state of the art performance. Additionally, we make our software available as an easy to use library.