Physics Informed Shallow Machine Learning for Wind Speed Prediction

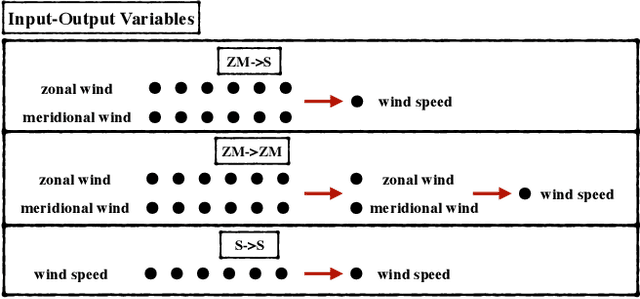
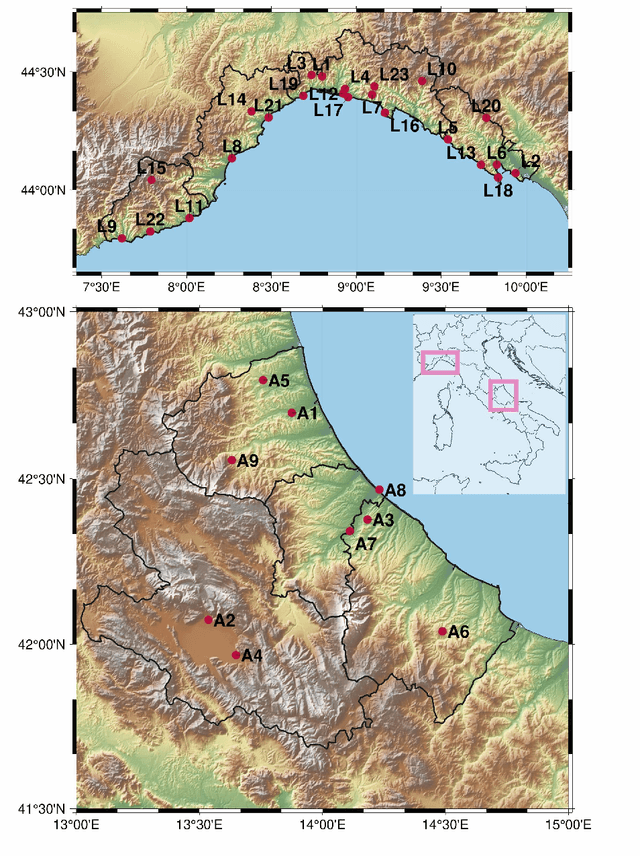
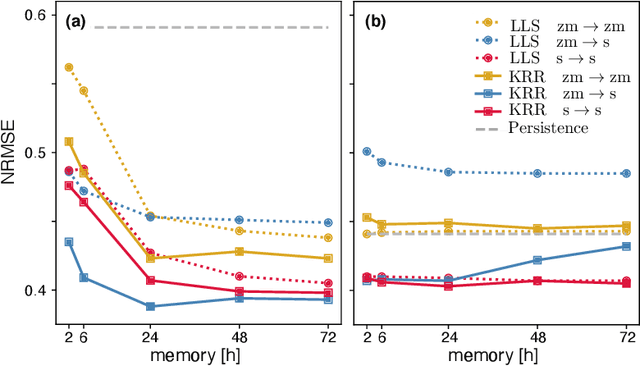
The ability to predict wind is crucial for both energy production and weather forecasting. Mechanistic models that form the basis of traditional forecasting perform poorly near the ground. In this paper, we take an alternative data-driven approach based on supervised learning. We analyze a massive dataset of wind measured from anemometers located at 10 m height in 32 locations in two central and north west regions of Italy (Abruzzo and Liguria). We train supervised learning algorithms using the past history of wind to predict its value at a future time (horizon). Using data from a single location and time horizon we compare systematically several algorithms where we vary the input/output variables, the memory of the input and the linear vs non-linear learning model. We then compare performance of the best algorithms across all locations and forecasting horizons. We find that the optimal design as well as its performance vary with the location. We demonstrate that the presence of a reproducible diurnal cycle provides a rationale to understand this variation. We conclude with a systematic comparison with state of the art algorithms and show that, when the model is accurately designed, shallow algorithms are competitive with more complex deep architectures.

Interpolation and Learning with Scale Dependent Kernels

We study the learning properties of nonparametric ridge-less least squares. In particular, we consider the common case of estimators defined by scale dependent kernels, and focus on the role of the scale. These estimators interpolate the data and the scale can be shown to control their stability through the condition number. Our analysis shows that are different regimes depending on the interplay between the sample size, its dimensions, and the smoothness of the problem. Indeed, when the sample size is less than exponential in the data dimension, then the scale can be chosen so that the learning error decreases. As the sample size becomes larger, the overall error stop decreasing but interestingly the scale can be chosen in such a way that the variance due to noise remains bounded. Our analysis combines, probabilistic results with a number of analytic techniques from interpolation theory.

Implicit Regularization of Accelerated Methods in Hilbert Spaces

We study learning properties of accelerated gradient descent methods for linear least-squares in Hilbert spaces. We analyze the implicit regularization properties of Nesterov acceleration and a variant of heavy-ball in terms of corresponding learning error bounds. Our results show that acceleration can provides faster bias decay than gradient descent, but also suffers of a more unstable behavior. As a result acceleration cannot be in general expected to improve learning accuracy with respect to gradient descent, but rather to achieve the same accuracy with reduced computations. Our theoretical results are validated by numerical simulations. Our analysis is based on studying suitable polynomials induced by the accelerated dynamics and combining spectral techniques with concentration inequalities.