Learning Controlled Stochastic Differential Equations

Identification of nonlinear dynamical systems is crucial across various fields, facilitating tasks such as control, prediction, optimization, and fault detection. Many applications require methods capable of handling complex systems while providing strong learning guarantees for safe and reliable performance. However, existing approaches often focus on simplified scenarios, such as deterministic models, known diffusion, discrete systems, one-dimensional dynamics, or systems constrained by strong structural assumptions such as linearity. This work proposes a novel method for estimating both drift and diffusion coefficients of continuous, multidimensional, nonlinear controlled stochastic differential equations with non-uniform diffusion. We assume regularity of the coefficients within a Sobolev space, allowing for broad applicability to various dynamical systems in robotics, finance, climate modeling, and biology. Leveraging the Fokker-Planck equation, we split the estimation into two tasks: (a) estimating system dynamics for a finite set of controls, and (b) estimating coefficients that govern those dynamics. We provide strong theoretical guarantees, including finite-sample bounds for \(L^2\), \(L^\infty\), and risk metrics, with learning rates adaptive to coefficients' regularity, similar to those in nonparametric least-squares regression literature. The practical effectiveness of our approach is demonstrated through extensive numerical experiments. Our method is available as an open-source Python library.

Generalization Bounds of Surrogate Policies for Combinatorial Optimization Problems

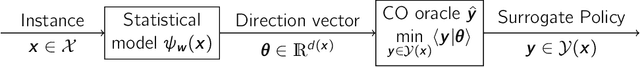
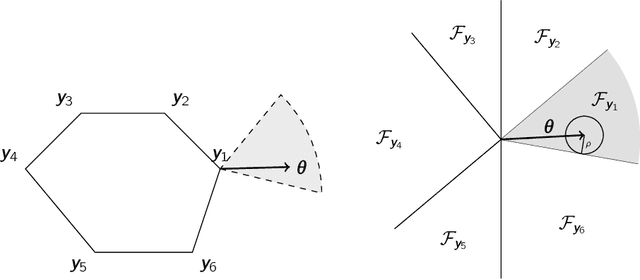
A recent stream of structured learning approaches has improved the practical state of the art for a range of combinatorial optimization problems with complex objectives encountered in operations research. Such approaches train policies that chain a statistical model with a surrogate combinatorial optimization oracle to map any instance of the problem to a feasible solution. The key idea is to exploit the statistical distribution over instances instead of dealing with instances separately. However learning such policies by risk minimization is challenging because the empirical risk is piecewise constant in the parameters, and few theoretical guarantees have been provided so far. In this article, we investigate methods that smooth the risk by perturbing the policy, which eases optimization and improves generalization. Our main contribution is a generalization bound that controls the perturbation bias, the statistical learning error, and the optimization error. Our analysis relies on the introduction of a uniform weak property, which captures and quantifies the interplay of the statistical model and the surrogate combinatorial optimization oracle. This property holds under mild assumptions on the statistical model, the surrogate optimization, and the instance data distribution. We illustrate the result on a range of applications such as stochastic vehicle scheduling. In particular, such policies are relevant for contextual stochastic optimization and our results cover this case.

Structured Prediction in Online Learning

We study a theoretical and algorithmic framework for structured prediction in the online learning setting. The problem of structured prediction, i.e. estimating function where the output space lacks a vectorial structure, is well studied in the literature of supervised statistical learning. We show that our algorithm is a generalisation of optimal algorithms from the supervised learning setting, and achieves the same excess risk upper bound also when data are not i.i.d. Moreover, we consider a second algorithm designed especially for non-stationary data distributions, including adversarial data. We bound its stochastic regret in function of the variation of the data distributions.

Closed-form Filtering for Non-linear Systems

Sequential Bayesian Filtering aims to estimate the current state distribution of a Hidden Markov Model, given the past observations. The problem is well-known to be intractable for most application domains, except in notable cases such as the tabular setting or for linear dynamical systems with gaussian noise. In this work, we propose a new class of filters based on Gaussian PSD Models, which offer several advantages in terms of density approximation and computational efficiency. We show that filtering can be efficiently performed in closed form when transitions and observations are Gaussian PSD Models. When the transition and observations are approximated by Gaussian PSD Models, we show that our proposed estimator enjoys strong theoretical guarantees, with estimation error that depends on the quality of the approximation and is adaptive to the regularity of the transition probabilities. In particular, we identify regimes in which our proposed filter attains a TV $\epsilon$-error with memory and computational complexity of $O(\epsilon^{-1})$ and $O(\epsilon^{-3/2})$ respectively, including the offline learning step, in contrast to the $O(\epsilon^{-2})$ complexity of sampling methods such as particle filtering.

GloptiNets: Scalable Non-Convex Optimization with Certificates

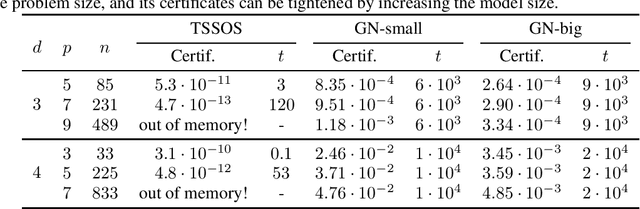
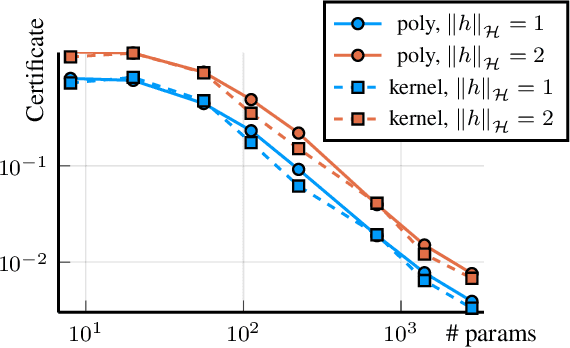
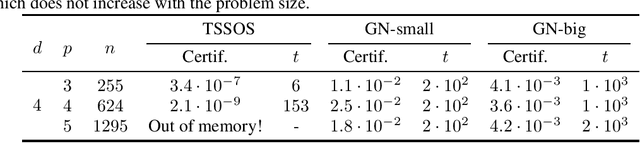
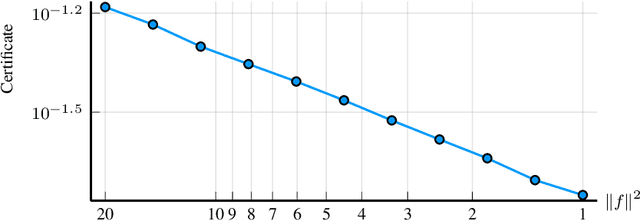
We present a novel approach to non-convex optimization with certificates, which handles smooth functions on the hypercube or on the torus. Unlike traditional methods that rely on algebraic properties, our algorithm exploits the regularity of the target function intrinsic in the decay of its Fourier spectrum. By defining a tractable family of models, we allow at the same time to obtain precise certificates and to leverage the advanced and powerful computational techniques developed to optimize neural networks. In this way the scalability of our approach is naturally enhanced by parallel computing with GPUs. Our approach, when applied to the case of polynomials of moderate dimensions but with thousands of coefficients, outperforms the state-of-the-art optimization methods with certificates, as the ones based on Lasserre's hierarchy, addressing problems intractable for the competitors.

Non-Parametric Learning of Stochastic Differential Equations with Fast Rates of Convergence

We propose a novel non-parametric learning paradigm for the identification of drift and diffusion coefficients of non-linear stochastic differential equations, which relies upon discrete-time observations of the state. The key idea essentially consists of fitting a RKHS-based approximation of the corresponding Fokker-Planck equation to such observations, yielding theoretical estimates of learning rates which, unlike previous works, become increasingly tighter when the regularity of the unknown drift and diffusion coefficients becomes higher. Our method being kernel-based, offline pre-processing may in principle be profitably leveraged to enable efficient numerical implementation.

Efficient Sampling of Stochastic Differential Equations with Positive Semi-Definite Models

This paper deals with the problem of efficient sampling from a stochastic differential equation, given the drift function and the diffusion matrix. The proposed approach leverages a recent model for probabilities \citep{rudi2021psd} (the positive semi-definite -- PSD model) from which it is possible to obtain independent and identically distributed (i.i.d.) samples at precision $\varepsilon$ with a cost that is $m^2 d \log(1/\varepsilon)$ where $m$ is the dimension of the model, $d$ the dimension of the space. The proposed approach consists in: first, computing the PSD model that satisfies the Fokker-Planck equation (or its fractional variant) associated with the SDE, up to error $\varepsilon$, and then sampling from the resulting PSD model. Assuming some regularity of the Fokker-Planck solution (i.e. $\beta$-times differentiability plus some geometric condition on its zeros) We obtain an algorithm that: (a) in the preparatory phase obtains a PSD model with L2 distance $\varepsilon$ from the solution of the equation, with a model of dimension $m = \varepsilon^{-(d+1)/(\beta-2s)} (\log(1/\varepsilon))^{d+1}$ where $0<s\leq1$ is the fractional power to the Laplacian, and total computational complexity of $O(m^{3.5} \log(1/\varepsilon))$ and then (b) for Fokker-Planck equation, it is able to produce i.i.d.\ samples with error $\varepsilon$ in Wasserstein-1 distance, with a cost that is $O(d \varepsilon^{-2(d+1)/\beta-2} \log(1/\varepsilon)^{2d+3})$ per sample. This means that, if the probability associated with the SDE is somewhat regular, i.e. $\beta \geq 4d+2$, then the algorithm requires $O(\varepsilon^{-0.88} \log(1/\varepsilon)^{4.5d})$ in the preparatory phase, and $O(\varepsilon^{-1/2}\log(1/\varepsilon)^{2d+2})$ for each sample. Our results suggest that as the true solution gets smoother, we can circumvent the curse of dimensionality without requiring any sort of convexity.

Approximation of optimization problems with constraints through kernel Sum-Of-Squares

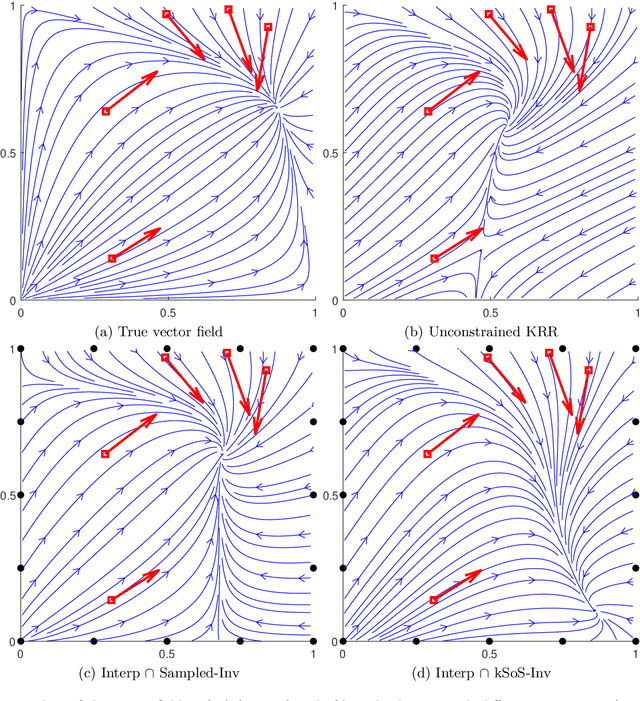
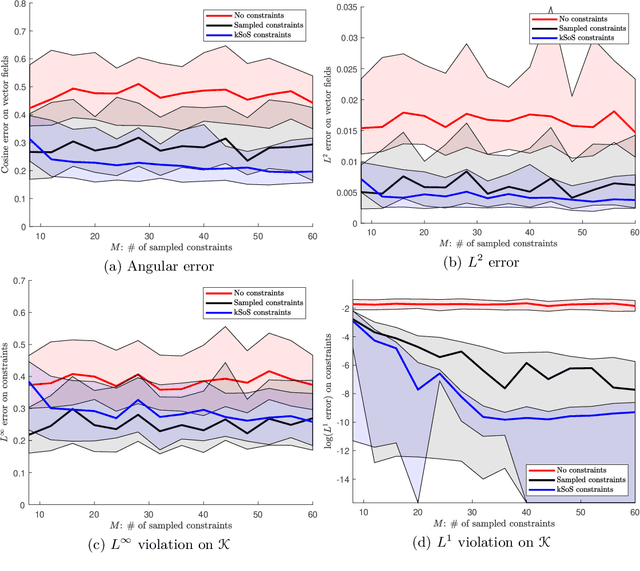
Handling an infinite number of inequality constraints in infinite-dimensional spaces occurs in many fields, from global optimization to optimal transport. These problems have been tackled individually in several previous articles through kernel Sum-Of-Squares (kSoS) approximations. We propose here a unified theorem to prove convergence guarantees for these schemes. Inequalities are turned into equalities to a class of nonnegative kSoS functions. This enables the use of scattering inequalities to mitigate the curse of dimensionality in sampling the constraints, leveraging the assumed smoothness of the functions appearing in the problem. This approach is illustrated in learning vector fields with side information, here the invariance of a set.

Vector-Valued Least-Squares Regression under Output Regularity Assumptions

We propose and analyse a reduced-rank method for solving least-squares regression problems with infinite dimensional output. We derive learning bounds for our method, and study under which setting statistical performance is improved in comparison to full-rank method. Our analysis extends the interest of reduced-rank regression beyond the standard low-rank setting to more general output regularity assumptions. We illustrate our theoretical insights on synthetic least-squares problems. Then, we propose a surrogate structured prediction method derived from this reduced-rank method. We assess its benefits on three different problems: image reconstruction, multi-label classification, and metabolite identification.

Active Labeling: Streaming Stochastic Gradients

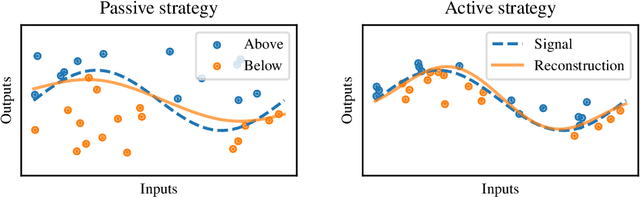
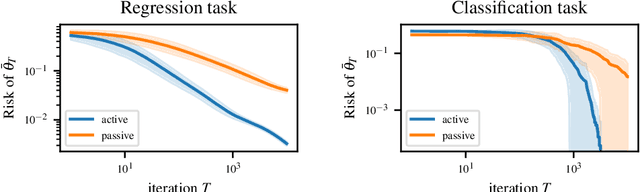
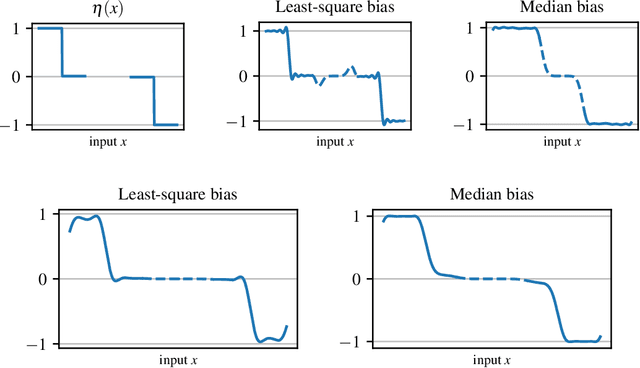
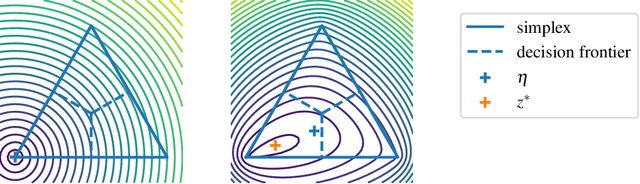
The workhorse of machine learning is stochastic gradient descent. To access stochastic gradients, it is common to consider iteratively input/output pairs of a training dataset. Interestingly, it appears that one does not need full supervision to access stochastic gradients, which is the main motivation of this paper. After formalizing the "active labeling" problem, which generalizes active learning based on partial supervision, we provide a streaming technique that provably minimizes the ratio of generalization error over number of samples. We illustrate our technique in depth for robust regression.