Anant Raj
SIERRA, Thoth
Distributed Perceptron under Bounded Staleness, Partial Participation, and Noisy Communication
Jan 15, 2026Abstract:We study a semi-asynchronous client-server perceptron trained via iterative parameter mixing (IPM-style averaging): clients run local perceptron updates and a server forms a global model by aggregating the updates that arrive in each communication round. The setting captures three system effects in federated and distributed deployments: (i) stale updates due to delayed model delivery and delayed application of client computations (two-sided version lag), (ii) partial participation (intermittent client availability), and (iii) imperfect communication on both downlink and uplink, modeled as effective zero-mean additive noise with bounded second moment. We introduce a server-side aggregation rule called staleness-bucket aggregation with padding that deterministically enforces a prescribed staleness profile over update ages without assuming any stochastic model for delays or participation. Under margin separability and bounded data radius, we prove a finite-horizon expected bound on the cumulative weighted number of perceptron mistakes over a given number of server rounds: the impact of delay appears only through the mean enforced staleness, whereas communication noise contributes an additional term that grows on the order of the square root of the horizon with the total noise energy. In the noiseless case, we show how a finite expected mistake budget yields an explicit finite-round stabilization bound under a mild fresh-participation condition.
Beyond Propagation of Chaos: A Stochastic Algorithm for Mean Field Optimization
Mar 17, 2025Abstract:Gradient flow in the 2-Wasserstein space is widely used to optimize functionals over probability distributions and is typically implemented using an interacting particle system with $n$ particles. Analyzing these algorithms requires showing (a) that the finite-particle system converges and/or (b) that the resultant empirical distribution of the particles closely approximates the optimal distribution (i.e., propagation of chaos). However, establishing efficient sufficient conditions can be challenging, as the finite particle system may produce heavily dependent random variables. In this work, we study the virtual particle stochastic approximation, originally introduced for Stein Variational Gradient Descent. This method can be viewed as a form of stochastic gradient descent in the Wasserstein space and can be implemented efficiently. In popular settings, we demonstrate that our algorithm's output converges to the optimal distribution under conditions similar to those for the infinite particle limit, and it produces i.i.d. samples without the need to explicitly establish propagation of chaos bounds.
Small steps no more: Global convergence of stochastic gradient bandits for arbitrary learning rates
Feb 11, 2025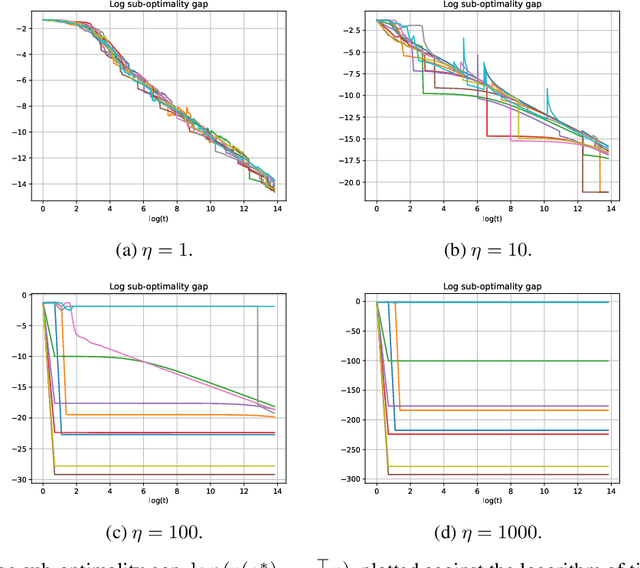
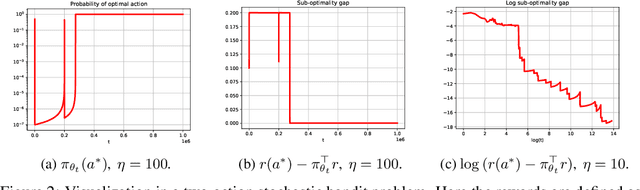
Abstract:We provide a new understanding of the stochastic gradient bandit algorithm by showing that it converges to a globally optimal policy almost surely using \emph{any} constant learning rate. This result demonstrates that the stochastic gradient algorithm continues to balance exploration and exploitation appropriately even in scenarios where standard smoothness and noise control assumptions break down. The proofs are based on novel findings about action sampling rates and the relationship between cumulative progress and noise, and extend the current understanding of how simple stochastic gradient methods behave in bandit settings.
Reweighting Improves Conditional Risk Bounds
Jan 04, 2025


Abstract:In this work, we study the weighted empirical risk minimization (weighted ERM) schema, in which an additional data-dependent weight function is incorporated when the empirical risk function is being minimized. We show that under a general ``balanceable" Bernstein condition, one can design a weighted ERM estimator to achieve superior performance in certain sub-regions over the one obtained from standard ERM, and the superiority manifests itself through a data-dependent constant term in the error bound. These sub-regions correspond to large-margin ones in classification settings and low-variance ones in heteroscedastic regression settings, respectively. Our findings are supported by evidence from synthetic data experiments.
Towards Principled, Practical Policy Gradient for Bandits and Tabular MDPs
May 21, 2024Abstract:We consider (stochastic) softmax policy gradient (PG) methods for bandits and tabular Markov decision processes (MDPs). While the PG objective is non-concave, recent research has used the objective's smoothness and gradient domination properties to achieve convergence to an optimal policy. However, these theoretical results require setting the algorithm parameters according to unknown problem-dependent quantities (e.g. the optimal action or the true reward vector in a bandit problem). To address this issue, we borrow ideas from the optimization literature to design practical, principled PG methods in both the exact and stochastic settings. In the exact setting, we employ an Armijo line-search to set the step-size for softmax PG and empirically demonstrate a linear convergence rate. In the stochastic setting, we utilize exponentially decreasing step-sizes, and characterize the convergence rate of the resulting algorithm. We show that the proposed algorithm offers similar theoretical guarantees as the state-of-the art results, but does not require the knowledge of oracle-like quantities. For the multi-armed bandit setting, our techniques result in a theoretically-principled PG algorithm that does not require explicit exploration, the knowledge of the reward gap, the reward distributions, or the noise. Finally, we empirically compare the proposed methods to PG approaches that require oracle knowledge, and demonstrate competitive performance.
Deep Generative Sampling in the Dual Divergence Space: A Data-efficient & Interpretative Approach for Generative AI
Apr 10, 2024



Abstract:Building on the remarkable achievements in generative sampling of natural images, we propose an innovative challenge, potentially overly ambitious, which involves generating samples of entire multivariate time series that resemble images. However, the statistical challenge lies in the small sample size, sometimes consisting of a few hundred subjects. This issue is especially problematic for deep generative models that follow the conventional approach of generating samples from a canonical distribution and then decoding or denoising them to match the true data distribution. In contrast, our method is grounded in information theory and aims to implicitly characterize the distribution of images, particularly the (global and local) dependency structure between pixels. We achieve this by empirically estimating its KL-divergence in the dual form with respect to the respective marginal distribution. This enables us to perform generative sampling directly in the optimized 1-D dual divergence space. Specifically, in the dual space, training samples representing the data distribution are embedded in the form of various clusters between two end points. In theory, any sample embedded between those two end points is in-distribution w.r.t. the data distribution. Our key idea for generating novel samples of images is to interpolate between the clusters via a walk as per gradients of the dual function w.r.t. the data dimensions. In addition to the data efficiency gained from direct sampling, we propose an algorithm that offers a significant reduction in sample complexity for estimating the divergence of the data distribution with respect to the marginal distribution. We provide strong theoretical guarantees along with an extensive empirical evaluation using many real-world datasets from diverse domains, establishing the superiority of our approach w.r.t. state-of-the-art deep learning methods.
From Inverse Optimization to Feasibility to ERM
Feb 27, 2024Abstract:Inverse optimization involves inferring unknown parameters of an optimization problem from known solutions, and is widely used in fields such as transportation, power systems and healthcare. We study the contextual inverse optimization setting that utilizes additional contextual information to better predict the unknown problem parameters. We focus on contextual inverse linear programming (CILP), addressing the challenges posed by the non-differentiable nature of LPs. For a linear prediction model, we reduce CILP to a convex feasibility problem allowing the use of standard algorithms such as alternating projections. The resulting algorithm for CILP is equipped with a linear convergence guarantee without additional assumptions such as degeneracy or interpolation. Next, we reduce CILP to empirical risk minimization (ERM) on a smooth, convex loss that satisfies the Polyak-Lojasiewicz condition. This reduction enables the use of scalable first-order optimization methods to solve large non-convex problems, while maintaining theoretical guarantees in the convex setting. Finally, we experimentally validate our approach on both synthetic and real-world problems, and demonstrate improved performance compared to existing methods.
Learning to Abstain From Uninformative Data
Sep 25, 2023Abstract:Learning and decision-making in domains with naturally high noise-to-signal ratio, such as Finance or Healthcare, is often challenging, while the stakes are very high. In this paper, we study the problem of learning and acting under a general noisy generative process. In this problem, the data distribution has a significant proportion of uninformative samples with high noise in the label, while part of the data contains useful information represented by low label noise. This dichotomy is present during both training and inference, which requires the proper handling of uninformative data during both training and testing. We propose a novel approach to learning under these conditions via a loss inspired by the selective learning theory. By minimizing this loss, the model is guaranteed to make a near-optimal decision by distinguishing informative data from uninformative data and making predictions. We build upon the strength of our theoretical guarantees by describing an iterative algorithm, which jointly optimizes both a predictor and a selector, and evaluates its empirical performance in a variety of settings.
Uniform-in-Time Wasserstein Stability Bounds for (Noisy) Stochastic Gradient Descent
May 20, 2023Abstract:Algorithmic stability is an important notion that has proven powerful for deriving generalization bounds for practical algorithms. The last decade has witnessed an increasing number of stability bounds for different algorithms applied on different classes of loss functions. While these bounds have illuminated various properties of optimization algorithms, the analysis of each case typically required a different proof technique with significantly different mathematical tools. In this study, we make a novel connection between learning theory and applied probability and introduce a unified guideline for proving Wasserstein stability bounds for stochastic optimization algorithms. We illustrate our approach on stochastic gradient descent (SGD) and we obtain time-uniform stability bounds (i.e., the bound does not increase with the number of iterations) for strongly convex losses and non-convex losses with additive noise, where we recover similar results to the prior art or extend them to more general cases by using a single proof technique. Our approach is flexible and can be generalizable to other popular optimizers, as it mainly requires developing Lyapunov functions, which are often readily available in the literature. It also illustrates that ergodicity is an important component for obtaining time-uniform bounds -- which might not be achieved for convex or non-convex losses unless additional noise is injected to the iterates. Finally, we slightly stretch our analysis technique and prove time-uniform bounds for SGD under convex and non-convex losses (without additional additive noise), which, to our knowledge, is novel.
Efficient Sampling of Stochastic Differential Equations with Positive Semi-Definite Models
Mar 30, 2023Abstract:This paper deals with the problem of efficient sampling from a stochastic differential equation, given the drift function and the diffusion matrix. The proposed approach leverages a recent model for probabilities \citep{rudi2021psd} (the positive semi-definite -- PSD model) from which it is possible to obtain independent and identically distributed (i.i.d.) samples at precision $\varepsilon$ with a cost that is $m^2 d \log(1/\varepsilon)$ where $m$ is the dimension of the model, $d$ the dimension of the space. The proposed approach consists in: first, computing the PSD model that satisfies the Fokker-Planck equation (or its fractional variant) associated with the SDE, up to error $\varepsilon$, and then sampling from the resulting PSD model. Assuming some regularity of the Fokker-Planck solution (i.e. $\beta$-times differentiability plus some geometric condition on its zeros) We obtain an algorithm that: (a) in the preparatory phase obtains a PSD model with L2 distance $\varepsilon$ from the solution of the equation, with a model of dimension $m = \varepsilon^{-(d+1)/(\beta-2s)} (\log(1/\varepsilon))^{d+1}$ where $0<s\leq1$ is the fractional power to the Laplacian, and total computational complexity of $O(m^{3.5} \log(1/\varepsilon))$ and then (b) for Fokker-Planck equation, it is able to produce i.i.d.\ samples with error $\varepsilon$ in Wasserstein-1 distance, with a cost that is $O(d \varepsilon^{-2(d+1)/\beta-2} \log(1/\varepsilon)^{2d+3})$ per sample. This means that, if the probability associated with the SDE is somewhat regular, i.e. $\beta \geq 4d+2$, then the algorithm requires $O(\varepsilon^{-0.88} \log(1/\varepsilon)^{4.5d})$ in the preparatory phase, and $O(\varepsilon^{-1/2}\log(1/\varepsilon)^{2d+2})$ for each sample. Our results suggest that as the true solution gets smoother, we can circumvent the curse of dimensionality without requiring any sort of convexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge