High-Order Langevin Monte Carlo Algorithms

Langevin algorithms are popular Markov chain Monte Carlo (MCMC) methods for large-scale sampling problems that often arise in data science. We propose Monte Carlo algorithms based on the discretizations of $P$-th order Langevin dynamics for any $P\geq 3$. Our design of $P$-th order Langevin Monte Carlo (LMC) algorithms is by combining splitting and accurate integration methods. We obtain Wasserstein convergence guarantees for sampling from distributions with log-concave and smooth densities. Specifically, the mixing time of the $P$-th order LMC algorithm scales as $O\left(d^{\frac{1}{R}}/\epsilon^{\frac{1}{2R}}\right)$ for $R=4\cdot 1_{\{ P=3\}}+ (2P-1)\cdot 1_{\{ P\geq 4\}}$, which has a better dependence on the dimension $d$ and the accuracy level $\epsilon$ as $P$ grows. Numerical experiments illustrate the efficiency of our proposed algorithms.

Accelerating Constrained Sampling: A Large Deviations Approach

The problem of sampling a target probability distribution on a constrained domain arises in many applications including machine learning. For constrained sampling, various Langevin algorithms such as projected Langevin Monte Carlo (PLMC) based on the discretization of reflected Langevin dynamics (RLD) and more generally skew-reflected non-reversible Langevin Monte Carlo (SRNLMC) based on the discretization of skew-reflected non-reversible Langevin dynamics (SRNLD) have been proposed and studied in the literature. This work focuses on the long-time behavior of SRNLD, where a skew-symmetric matrix is added to RLD. Although the non-asymptotic convergence analysis for SRNLD (and SRNLMC) and the acceleration compared to RLD (and PMLC) have been studied in the literature, it is not clear how one should design the skew-symmetric matrix in the dynamics to achieve good performance in practice. We establish a large deviation principle (LDP) for the empirical measure of SRNLD when the skew-symmetric matrix is chosen such that its product with the inward unit normal vector field on the boundary is zero. By explicitly characterizing the rate functions, we show that SRNLD can accelerate the convergence to the target distribution compared to RLD with this choice of the skew-symmetric matrix. Numerical experiments for SRNLMC based on the proposed skew-symmetric matrix show superior performance which validate the theoretical findings from the large deviations theory.

Accelerating Langevin Monte Carlo Sampling: A Large Deviations Analysis

Langevin algorithms are popular Markov chain Monte Carlo methods that are often used to solve high-dimensional large-scale sampling problems in machine learning. The most classical Langevin Monte Carlo algorithm is based on the overdamped Langevin dynamics. There are many variants of Langevin dynamics that often show superior performance in practice. In this paper, we provide a unified approach to study the acceleration of the variants of the overdamped Langevin dynamics through the lens of large deviations theory. Numerical experiments using both synthetic and real data are provided to illustrate the efficiency of these variants.

BRIDLE: Generalized Self-supervised Learning with Quantization

Self-supervised learning has been a powerful approach for learning meaningful representations from unlabeled data across various domains, reducing the reliance on large labeled datasets. Inspired by BERT's success in capturing deep bidirectional contexts in natural language processing, similar frameworks have been adapted to other modalities such as audio, with models like BEATs extending the bidirectional training paradigm to audio signals using vector quantization (VQ). However, these frameworks face challenges, notably their dependence on a single codebook for quantization, which may not capture the complex, multifaceted nature of signals. In addition, inefficiencies in codebook utilization lead to underutilized code vectors. To address these limitations, we introduce BRIDLE (Bidirectional Residual Quantization Interleaved Discrete Learning Encoder), a self-supervised encoder pretraining framework that incorporates residual quantization (RQ) into the bidirectional training process, and is generalized for pretraining with audio, image, and video. Using multiple hierarchical codebooks, RQ enables fine-grained discretization in the latent space, enhancing representation quality. BRIDLE involves an interleaved training procedure between the encoder and tokenizer. We evaluate BRIDLE on audio understanding tasks using classification benchmarks, achieving state-of-the-art results, and demonstrate competitive performance on image classification and video classification tasks, showing consistent improvements over traditional VQ methods in downstream performance.

Algorithmic Stability of Stochastic Gradient Descent with Momentum under Heavy-Tailed Noise

Understanding the generalization properties of optimization algorithms under heavy-tailed noise has gained growing attention. However, the existing theoretical results mainly focus on stochastic gradient descent (SGD) and the analysis of heavy-tailed optimizers beyond SGD is still missing. In this work, we establish generalization bounds for SGD with momentum (SGDm) under heavy-tailed gradient noise. We first consider the continuous-time limit of SGDm, i.e., a Levy-driven stochastic differential equation (SDE), and establish quantitative Wasserstein algorithmic stability bounds for a class of potentially non-convex loss functions. Our bounds reveal a remarkable observation: For quadratic loss functions, we show that SGDm admits a worse generalization bound in the presence of heavy-tailed noise, indicating that the interaction of momentum and heavy tails can be harmful for generalization. We then extend our analysis to discrete-time and develop a uniform-in-time discretization error bound, which, to our knowledge, is the first result of its kind for SDEs with degenerate noise. This result shows that, with appropriately chosen step-sizes, the discrete dynamics retain the generalization properties of the limiting SDE. We illustrate our theory on both synthetic quadratic problems and neural networks.

Non-Reversible Langevin Algorithms for Constrained Sampling

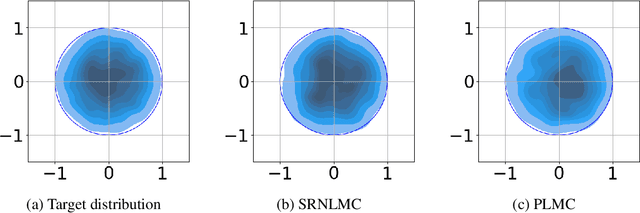
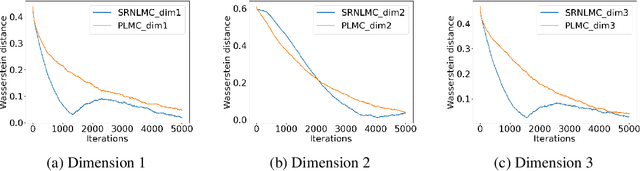
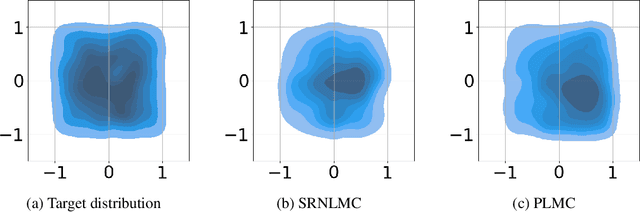
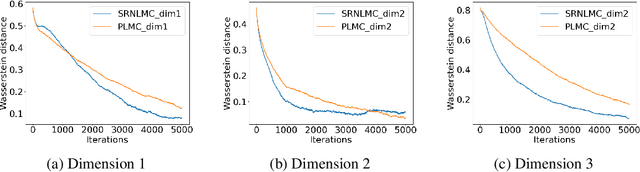
We consider the constrained sampling problem where the goal is to sample from a target distribution on a constrained domain. We propose skew-reflected non-reversible Langevin dynamics (SRNLD), a continuous-time stochastic differential equation with skew-reflected boundary. We obtain non-asymptotic convergence rate of SRNLD to the target distribution in both total variation and 1-Wasserstein distances. By breaking reversibility, we show that the convergence is faster than the special case of the reversible dynamics. Based on the discretization of SRNLD, we propose skew-reflected non-reversible Langevin Monte Carlo (SRNLMC), and obtain non-asymptotic discretization error from SRNLD, and convergence guarantees to the target distribution in 1-Wasserstein distance. We show better performance guarantees than the projected Langevin Monte Carlo in the literature that is based on the reversible dynamics. Numerical experiments are provided for both synthetic and real datasets to show efficiency of the proposed algorithms.

Generalized EXTRA stochastic gradient Langevin dynamics

Langevin algorithms are popular Markov Chain Monte Carlo methods for Bayesian learning, particularly when the aim is to sample from the posterior distribution of a parametric model, given the input data and the prior distribution over the model parameters. Their stochastic versions such as stochastic gradient Langevin dynamics (SGLD) allow iterative learning based on randomly sampled mini-batches of large datasets and are scalable to large datasets. However, when data is decentralized across a network of agents subject to communication and privacy constraints, standard SGLD algorithms cannot be applied. Instead, we employ decentralized SGLD (DE-SGLD) algorithms, where Bayesian learning is performed collaboratively by a network of agents without sharing individual data. Nonetheless, existing DE-SGLD algorithms induce a bias at every agent that can negatively impact performance; this bias persists even when using full batches and is attributable to network effects. Motivated by the EXTRA algorithm and its generalizations for decentralized optimization, we propose the generalized EXTRA stochastic gradient Langevin dynamics, which eliminates this bias in the full-batch setting. Moreover, we show that, in the mini-batch setting, our algorithm provides performance bounds that significantly improve upon those of standard DE-SGLD algorithms in the literature. Our numerical results also demonstrate the efficiency of the proposed approach.

Differential Privacy of Noisy GD under Heavy-Tailed Perturbations

Injecting heavy-tailed noise to the iterates of stochastic gradient descent (SGD) has received increasing attention over the past few years. While various theoretical properties of the resulting algorithm have been analyzed mainly from learning theory and optimization perspectives, their privacy preservation properties have not yet been established. Aiming to bridge this gap, we provide differential privacy (DP) guarantees for noisy SGD, when the injected noise follows an $\alpha$-stable distribution, which includes a spectrum of heavy-tailed distributions (with infinite variance) as well as the Gaussian distribution. Considering the $(\epsilon, \delta)$-DP framework, we show that SGD with heavy-tailed perturbations achieves $(0, \tilde{\mathcal{O}}(1/n))$-DP for a broad class of loss functions which can be non-convex, where $n$ is the number of data points. As a remarkable byproduct, contrary to prior work that necessitates bounded sensitivity for the gradients or clipping the iterates, our theory reveals that under mild assumptions, such a projection step is not actually necessary. We illustrate that the heavy-tailed noising mechanism achieves similar DP guarantees compared to the Gaussian case, which suggests that it can be a viable alternative to its light-tailed counterparts.

Intriguing Differences Between Zero-Shot and Systematic Evaluations of Vision-Language Transformer Models

Transformer-based models have dominated natural language processing and other areas in the last few years due to their superior (zero-shot) performance on benchmark datasets. However, these models are poorly understood due to their complexity and size. While probing-based methods are widely used to understand specific properties, the structures of the representation space are not systematically characterized; consequently, it is unclear how such models generalize and overgeneralize to new inputs beyond datasets. In this paper, based on a new gradient descent optimization method, we are able to explore the embedding space of a commonly used vision-language model. Using the Imagenette dataset, we show that while the model achieves over 99\% zero-shot classification performance, it fails systematic evaluations completely. Using a linear approximation, we provide a framework to explain the striking differences. We have also obtained similar results using a different model to support that our results are applicable to other transformer models with continuous inputs. We also propose a robust way to detect the modified images.

Convergence Analysis for General Probability Flow ODEs of Diffusion Models in Wasserstein Distances

Score-based generative modeling with probability flow ordinary differential equations (ODEs) has achieved remarkable success in a variety of applications. While various fast ODE-based samplers have been proposed in the literature and employed in practice, the theoretical understandings about convergence properties of the probability flow ODE are still quite limited. In this paper, we provide the first non-asymptotic convergence analysis for a general class of probability flow ODE samplers in 2-Wasserstein distance, assuming accurate score estimates. We then consider various examples and establish results on the iteration complexity of the corresponding ODE-based samplers.