Factor-Based Conditional Diffusion Model for Portfolio Optimization

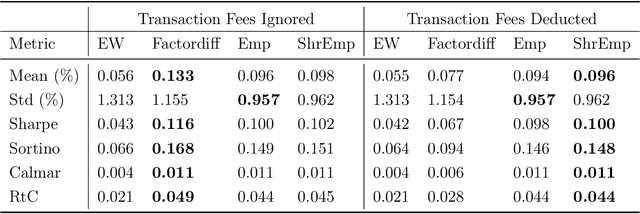
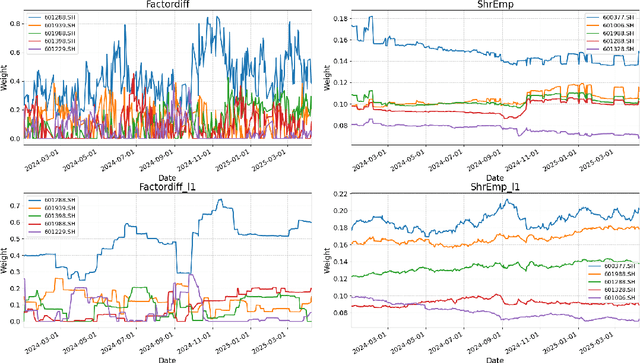
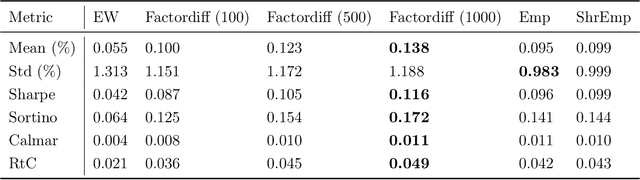
We propose a novel conditional diffusion model for portfolio optimization that learns the cross-sectional distribution of next-day stock returns conditioned on asset-specific factors. The model builds on the Diffusion Transformer with token-wise conditioning, linking each asset's return to its own factor vector while capturing cross-asset dependencies. Generated return samples are used for daily mean-variance optimization under realistic constraints. Empirical results on the Chinese A-share market show that our approach consistently outperforms benchmark methods based on standard empirical and shrinkage-based estimators across multiple metrics.

Data-driven generative simulation of SDEs using diffusion models

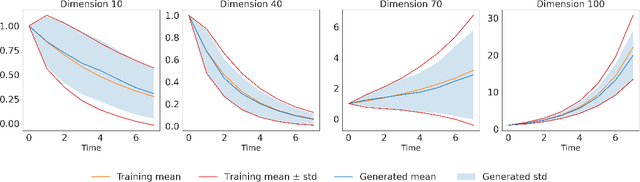
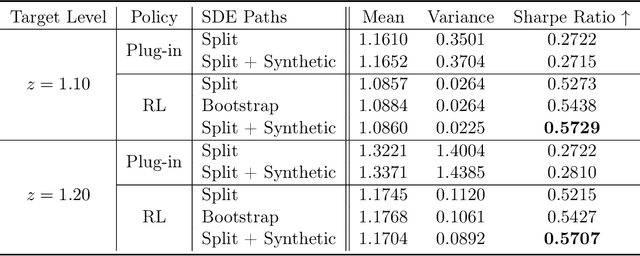
This paper introduces a new approach to generating sample paths of unknown stochastic differential equations (SDEs) using diffusion models, a class of generative AI models commonly employed in image and video applications. Unlike the traditional Monte Carlo methods for simulating SDEs, which require explicit specifications of the drift and diffusion coefficients, our method takes a model-free, data-driven approach. Given a finite set of sample paths from an SDE, we utilize conditional diffusion models to generate new, synthetic paths of the same SDE. To demonstrate the effectiveness of our approach, we conduct a simulation experiment to compare our method with alternative benchmark ones including neural SDEs. Furthermore, in an empirical study we leverage these synthetically generated sample paths to enhance the performance of reinforcement learning algorithms for continuous-time mean-variance portfolio selection, hinting promising applications of diffusion models in financial analysis and decision-making.

Reward-Directed Score-Based Diffusion Models via q-Learning

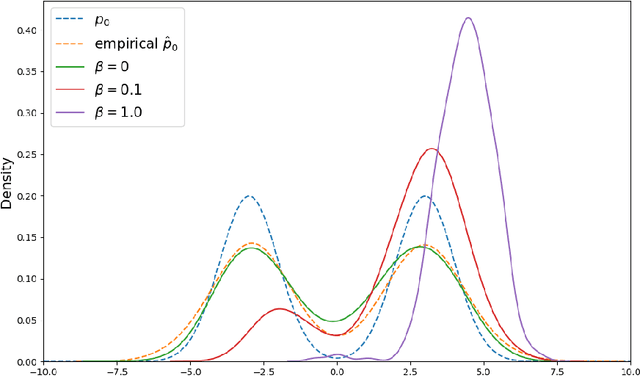
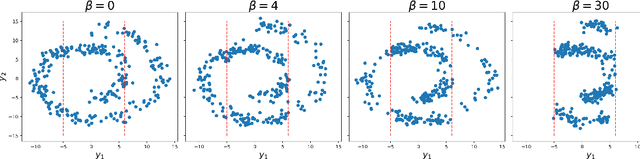
We propose a new reinforcement learning (RL) formulation for training continuous-time score-based diffusion models for generative AI to generate samples that maximize reward functions while keeping the generated distributions close to the unknown target data distributions. Different from most existing studies, our formulation does not involve any pretrained model for the unknown score functions of the noise-perturbed data distributions. We present an entropy-regularized continuous-time RL problem and show that the optimal stochastic policy has a Gaussian distribution with a known covariance matrix. Based on this result, we parameterize the mean of Gaussian policies and develop an actor-critic type (little) q-learning algorithm to solve the RL problem. A key ingredient in our algorithm design is to obtain noisy observations from the unknown score function via a ratio estimator. Numerically, we show the effectiveness of our approach by comparing its performance with two state-of-the-art RL methods that fine-tune pretrained models. Finally, we discuss extensions of our RL formulation to probability flow ODE implementation of diffusion models and to conditional diffusion models.

Regret Bounds for Episodic Risk-Sensitive Linear Quadratic Regulator

Risk-sensitive linear quadratic regulator is one of the most fundamental problems in risk-sensitive optimal control. In this paper, we study online adaptive control of risk-sensitive linear quadratic regulator in the finite horizon episodic setting. We propose a simple least-squares greedy algorithm and show that it achieves $\widetilde{\mathcal{O}}(\log N)$ regret under a specific identifiability assumption, where $N$ is the total number of episodes. If the identifiability assumption is not satisfied, we propose incorporating exploration noise into the least-squares-based algorithm, resulting in an algorithm with $\widetilde{\mathcal{O}}(\sqrt{N})$ regret. To our best knowledge, this is the first set of regret bounds for episodic risk-sensitive linear quadratic regulator. Our proof relies on perturbation analysis of less-standard Riccati equations for risk-sensitive linear quadratic control, and a delicate analysis of the loss in the risk-sensitive performance criterion due to applying the suboptimal controller in the online learning process.

Reinforcement Learning for Intensity Control: An Application to Choice-Based Network Revenue Management

Intensity control is a type of continuous-time dynamic optimization problems with many important applications in Operations Research including queueing and revenue management. In this study, we adapt the reinforcement learning framework to intensity control using choice-based network revenue management as a case study, which is a classical problem in revenue management that features a large state space, a large action space and a continuous time horizon. We show that by utilizing the inherent discretization of the sample paths created by the jump points, a unique and defining feature of intensity control, one does not need to discretize the time horizon in advance, which was believed to be necessary because most reinforcement learning algorithms are designed for discrete-time problems. As a result, the computation can be facilitated and the discretization error is significantly reduced. We lay the theoretical foundation for the Monte Carlo and temporal difference learning algorithms for policy evaluation and develop policy gradient based actor critic algorithms for intensity control. Via a comprehensive numerical study, we demonstrate the benefit of our approach versus other state-of-the-art benchmarks.

Reinforcement Learning for Jump-Diffusions

We study continuous-time reinforcement learning (RL) for stochastic control in which system dynamics are governed by jump-diffusion processes. We formulate an entropy-regularized exploratory control problem with stochastic policies to capture the exploration--exploitation balance essential for RL. Unlike the pure diffusion case initially studied by Wang et al. (2020), the derivation of the exploratory dynamics under jump-diffusions calls for a careful formulation of the jump part. Through a theoretical analysis, we find that one can simply use the same policy evaluation and q-learning algorithms in Jia and Zhou (2022a, 2023), originally developed for controlled diffusions, without needing to check a priori whether the underlying data come from a pure diffusion or a jump-diffusion. However, we show that the presence of jumps ought to affect parameterizations of actors and critics in general. Finally, we investigate as an application the mean-variance portfolio selection problem with stock price modelled as a jump-diffusion, and show that both RL algorithms and parameterizations are invariant with respect to jumps.

No Algorithmic Collusion in Two-Player Blindfolded Game with Thompson Sampling

When two players are engaged in a repeated game with unknown payoff matrices, they may be completely unaware of the existence of each other and use multi-armed bandit algorithms to choose the actions, which is referred to as the ``blindfolded game'' in this paper. We show that when the players use Thompson sampling, the game dynamics converges to the Nash equilibrium under a mild assumption on the payoff matrices. Therefore, algorithmic collusion doesn't arise in this case despite the fact that the players do not intentionally deploy competitive strategies. To prove the convergence result, we find that the framework developed in stochastic approximation doesn't apply, because of the sporadic and infrequent updates of the inferior actions and the lack of Lipschitz continuity. We develop a novel sample-path-wise approach to show the convergence.

Convergence Analysis for General Probability Flow ODEs of Diffusion Models in Wasserstein Distances

Score-based generative modeling with probability flow ordinary differential equations (ODEs) has achieved remarkable success in a variety of applications. While various fast ODE-based samplers have been proposed in the literature and employed in practice, the theoretical understandings about convergence properties of the probability flow ODE are still quite limited. In this paper, we provide the first non-asymptotic convergence analysis for a general class of probability flow ODE samplers in 2-Wasserstein distance, assuming accurate score estimates. We then consider various examples and establish results on the iteration complexity of the corresponding ODE-based samplers.

Wasserstein Convergence Guarantees for a General Class of Score-Based Generative Models

Score-based generative models (SGMs) is a recent class of deep generative models with state-of-the-art performance in many applications. In this paper, we establish convergence guarantees for a general class of SGMs in 2-Wasserstein distance, assuming accurate score estimates and smooth log-concave data distribution. We specialize our result to several concrete SGMs with specific choices of forward processes modelled by stochastic differential equations, and obtain an upper bound on the iteration complexity for each model, which demonstrates the impacts of different choices of the forward processes. We also provide a lower bound when the data distribution is Gaussian. Numerically, we experiment SGMs with different forward processes, some of which are newly proposed in this paper, for unconditional image generation on CIFAR-10. We find that the experimental results are in good agreement with our theoretical predictions on the iteration complexity, and the models with our newly proposed forward processes can outperform existing models.

Regret Bounds for Markov Decision Processes with Recursive Optimized Certainty Equivalents

The optimized certainty equivalent (OCE) is a family of risk measures that cover important examples such as entropic risk, conditional value-at-risk and mean-variance models. In this paper, we propose a new episodic risk-sensitive reinforcement learning formulation based on tabular Markov decision processes with recursive OCEs. We design an efficient learning algorithm for this problem based on value iteration and upper confidence bound. We derive an upper bound on the regret of the proposed algorithm, and also establish a minimax lower bound. Our bounds show that the regret rate achieved by our proposed algorithm has optimal dependence on the number of episodes and the number of actions.