Xun Yu Zhou
Data-driven generative simulation of SDEs using diffusion models
Sep 10, 2025
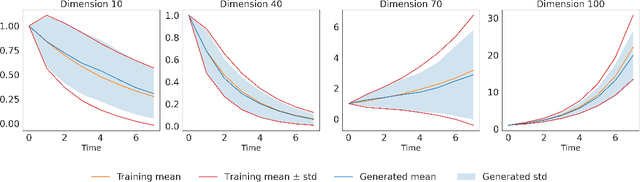
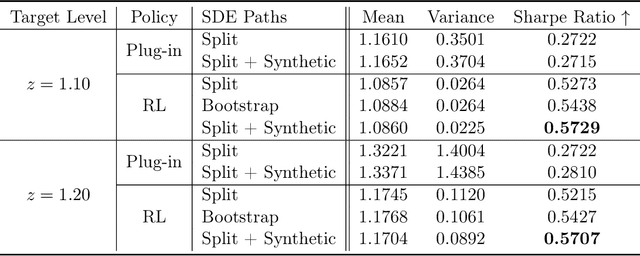
Abstract:This paper introduces a new approach to generating sample paths of unknown stochastic differential equations (SDEs) using diffusion models, a class of generative AI models commonly employed in image and video applications. Unlike the traditional Monte Carlo methods for simulating SDEs, which require explicit specifications of the drift and diffusion coefficients, our method takes a model-free, data-driven approach. Given a finite set of sample paths from an SDE, we utilize conditional diffusion models to generate new, synthetic paths of the same SDE. To demonstrate the effectiveness of our approach, we conduct a simulation experiment to compare our method with alternative benchmark ones including neural SDEs. Furthermore, in an empirical study we leverage these synthetically generated sample paths to enhance the performance of reinforcement learning algorithms for continuous-time mean-variance portfolio selection, hinting promising applications of diffusion models in financial analysis and decision-making.
Regret of exploratory policy improvement and $q$-learning
Nov 02, 2024
Abstract:We study the convergence of $q$-learning and related algorithms introduced by Jia and Zhou (J. Mach. Learn. Res., 24 (2023), 161) for controlled diffusion processes. Under suitable conditions on the growth and regularity of the model parameters, we provide a quantitative error and regret analysis of both the exploratory policy improvement algorithm and the $q$-learning algorithm.
Reward-Directed Score-Based Diffusion Models via q-Learning
Sep 07, 2024
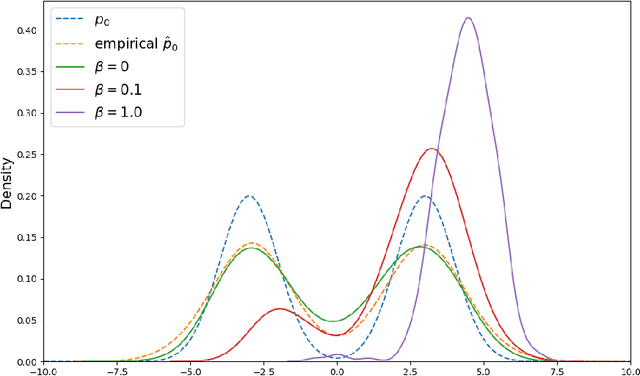
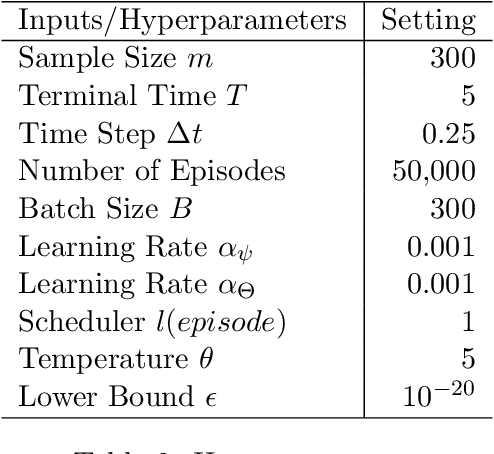
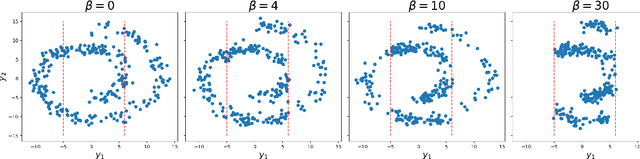
Abstract:We propose a new reinforcement learning (RL) formulation for training continuous-time score-based diffusion models for generative AI to generate samples that maximize reward functions while keeping the generated distributions close to the unknown target data distributions. Different from most existing studies, our formulation does not involve any pretrained model for the unknown score functions of the noise-perturbed data distributions. We present an entropy-regularized continuous-time RL problem and show that the optimal stochastic policy has a Gaussian distribution with a known covariance matrix. Based on this result, we parameterize the mean of Gaussian policies and develop an actor-critic type (little) q-learning algorithm to solve the RL problem. A key ingredient in our algorithm design is to obtain noisy observations from the unknown score function via a ratio estimator. Numerically, we show the effectiveness of our approach by comparing its performance with two state-of-the-art RL methods that fine-tune pretrained models. Finally, we discuss extensions of our RL formulation to probability flow ODE implementation of diffusion models and to conditional diffusion models.
Sublinear Regret for An Actor-Critic Algorithm in Continuous-Time Linear-Quadratic Reinforcement Learning
Jul 24, 2024Abstract:We study reinforcement learning (RL) for a class of continuous-time linear-quadratic (LQ) control problems for diffusions where volatility of the state processes depends on both state and control variables. We apply a model-free approach that relies neither on knowledge of model parameters nor on their estimations, and devise an actor-critic algorithm to learn the optimal policy parameter directly. Our main contributions include the introduction of a novel exploration schedule and a regret analysis of the proposed algorithm. We provide the convergence rate of the policy parameter to the optimal one, and prove that the algorithm achieves a regret bound of $O(N^{\frac{3}{4}})$ up to a logarithmic factor. We conduct a simulation study to validate the theoretical results and demonstrate the effectiveness and reliability of the proposed algorithm. We also perform numerical comparisons between our method and those of the recent model-based stochastic LQ RL studies adapted to the state- and control-dependent volatility setting, demonstrating a better performance of the former in terms of regret bounds.
Reinforcement Learning for Jump-Diffusions
May 26, 2024Abstract:We study continuous-time reinforcement learning (RL) for stochastic control in which system dynamics are governed by jump-diffusion processes. We formulate an entropy-regularized exploratory control problem with stochastic policies to capture the exploration--exploitation balance essential for RL. Unlike the pure diffusion case initially studied by Wang et al. (2020), the derivation of the exploratory dynamics under jump-diffusions calls for a careful formulation of the jump part. Through a theoretical analysis, we find that one can simply use the same policy evaluation and q-learning algorithms in Jia and Zhou (2022a, 2023), originally developed for controlled diffusions, without needing to check a priori whether the underlying data come from a pure diffusion or a jump-diffusion. However, we show that the presence of jumps ought to affect parameterizations of actors and critics in general. Finally, we investigate as an application the mean-variance portfolio selection problem with stock price modelled as a jump-diffusion, and show that both RL algorithms and parameterizations are invariant with respect to jumps.
Learning Merton's Strategies in an Incomplete Market: Recursive Entropy Regularization and Biased Gaussian Exploration
Dec 19, 2023Abstract:We study Merton's expected utility maximization problem in an incomplete market, characterized by a factor process in addition to the stock price process, where all the model primitives are unknown. We take the reinforcement learning (RL) approach to learn optimal portfolio policies directly by exploring the unknown market, without attempting to estimate the model parameters. Based on the entropy-regularization framework for general continuous-time RL formulated in Wang et al. (2020), we propose a recursive weighting scheme on exploration that endogenously discounts the current exploration reward by the past accumulative amount of exploration. Such a recursive regularization restores the optimality of Gaussian exploration. However, contrary to the existing results, the optimal Gaussian policy turns out to be biased in general, due to the interwinding needs for hedging and for exploration. We present an asymptotic analysis of the resulting errors to show how the level of exploration affects the learned policies. Furthermore, we establish a policy improvement theorem and design several RL algorithms to learn Merton's optimal strategies. At last, we carry out both simulation and empirical studies with a stochastic volatility environment to demonstrate the efficiency and robustness of the RL algorithms in comparison to the conventional plug-in method.
Variable Clustering via Distributionally Robust Nodewise Regression
Dec 21, 2022



Abstract:We study a multi-factor block model for variable clustering and connect it to the regularized subspace clustering by formulating a distributionally robust version of the nodewise regression. To solve the latter problem, we derive a convex relaxation, provide guidance on selecting the size of the robust region, and hence the regularization weighting parameter, based on the data, and propose an ADMM algorithm for implementation. We validate our method in an extensive simulation study. Finally, we propose and apply a variant of our method to stock return data, obtain interpretable clusters that facilitate portfolio selection and compare its out-of-sample performance with other clustering methods in an empirical study.
Square-root regret bounds for continuous-time episodic Markov decision processes
Oct 03, 2022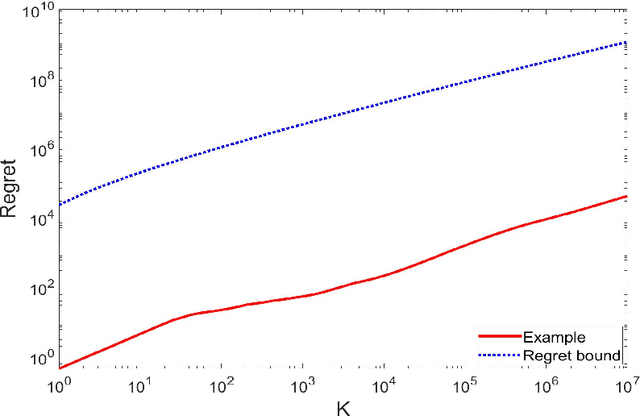
Abstract:We study reinforcement learning for continuous-time Markov decision processes (MDPs) in the finite-horizon episodic setting. We present a learning algorithm based on the methods of value iteration and upper confidence bound. We derive an upper bound on the worst-case expected regret for the proposed algorithm, and establish a worst-case lower bound, both bounds are of the order of square-root on the number of episodes. Finally, we conduct simulation experiments to illustrate the performance of our algorithm.
Choquet regularization for reinforcement learning
Aug 17, 2022

Abstract:We propose \emph{Choquet regularizers} to measure and manage the level of exploration for reinforcement learning (RL), and reformulate the continuous-time entropy-regularized RL problem of Wang et al. (2020, JMLR, 21(198)) in which we replace the differential entropy used for regularization with a Choquet regularizer. We derive the Hamilton--Jacobi--Bellman equation of the problem, and solve it explicitly in the linear--quadratic (LQ) case via maximizing statically a mean--variance constrained Choquet regularizer. Under the LQ setting, we derive explicit optimal distributions for several specific Choquet regularizers, and conversely identify the Choquet regularizers that generate a number of broadly used exploratory samplers such as $\epsilon$-greedy, exponential, uniform and Gaussian.
q-Learning in Continuous Time
Jul 02, 2022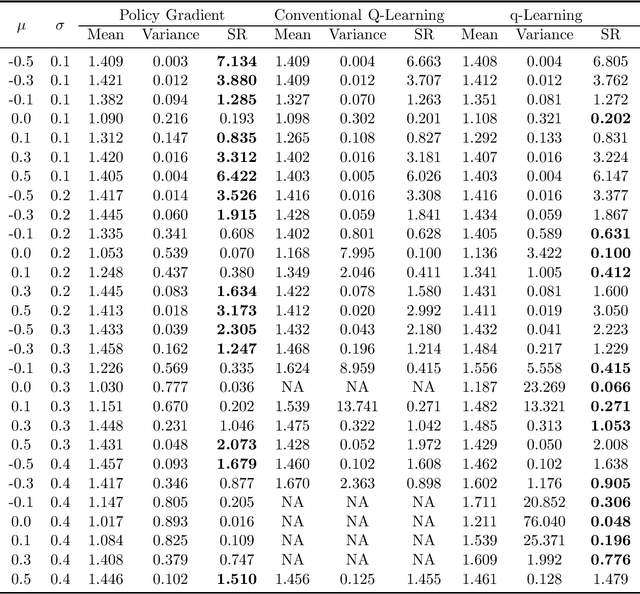
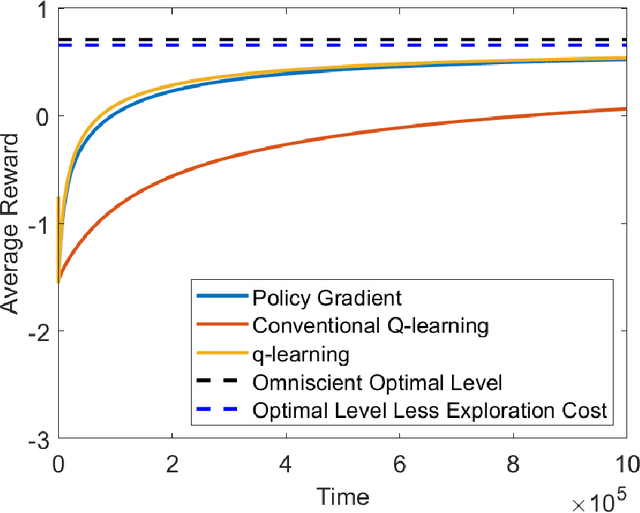

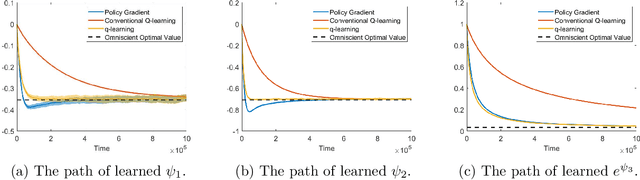
Abstract:We study the continuous-time counterpart of Q-learning for reinforcement learning (RL) under the entropy-regularized, exploratory diffusion process formulation introduced by Wang et al. (2020) As the conventional (big) Q-function collapses in continuous time, we consider its first-order approximation and coin the term "(little) q-function". This function is related to the instantaneous advantage rate function as well as the Hamiltonian. We develop a "q-learning" theory around the q-function that is independent of time discretization. Given a stochastic policy, we jointly characterize the associated q-function and value function by martingale conditions of certain stochastic processes. We then apply the theory to devise different actor-critic algorithms for solving underlying RL problems, depending on whether or not the density function of the Gibbs measure generated from the q-function can be computed explicitly. One of our algorithms interprets the well-known Q-learning algorithm SARSA, and another recovers a policy gradient (PG) based continuous-time algorithm proposed in Jia and Zhou (2021). Finally, we conduct simulation experiments to compare the performance of our algorithms with those of PG-based algorithms in Jia and Zhou (2021) and time-discretized conventional Q-learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge