A Similarity Measure Between Functions with Applications to Statistical Learning and Optimization

In this note, we present a novel measure of similarity between two functions. It quantifies how the sub-optimality gaps of two functions convert to each other, and unifies several existing notions of functional similarity. We show that it has convenient operation rules, and illustrate its use in empirical risk minimization and non-stationary online optimization.

A Particle Algorithm for Mean-Field Variational Inference

Variational inference is a fast and scalable alternative to Markov chain Monte Carlo and has been widely applied to posterior inference tasks in statistics and machine learning. A traditional approach for implementing mean-field variational inference (MFVI) is coordinate ascent variational inference (CAVI), which relies crucially on parametric assumptions on complete conditionals. In this paper, we introduce a novel particle-based algorithm for mean-field variational inference, which we term PArticle VI (PAVI). Notably, our algorithm does not rely on parametric assumptions on complete conditionals, and it applies to the nonparametric setting. We provide non-asymptotic finite-particle convergence guarantee for our algorithm. To our knowledge, this is the first end-to-end guarantee for particle-based MFVI.

Localized exploration in contextual dynamic pricing achieves dimension-free regret

We study the problem of contextual dynamic pricing with a linear demand model. We propose a novel localized exploration-then-commit (LetC) algorithm which starts with a pure exploration stage, followed by a refinement stage that explores near the learned optimal pricing policy, and finally enters a pure exploitation stage. The algorithm is shown to achieve a minimax optimal, dimension-free regret bound when the time horizon exceeds a polynomial of the covariate dimension. Furthermore, we provide a general theoretical framework that encompasses the entire time spectrum, demonstrating how to balance exploration and exploitation when the horizon is limited. The analysis is powered by a novel critical inequality that depicts the exploration-exploitation trade-off in dynamic pricing, mirroring its existing counterpart for the bias-variance trade-off in regularized regression. Our theoretical results are validated by extensive experiments on synthetic and real-world data.

Adaptive Transfer Clustering: A Unified Framework

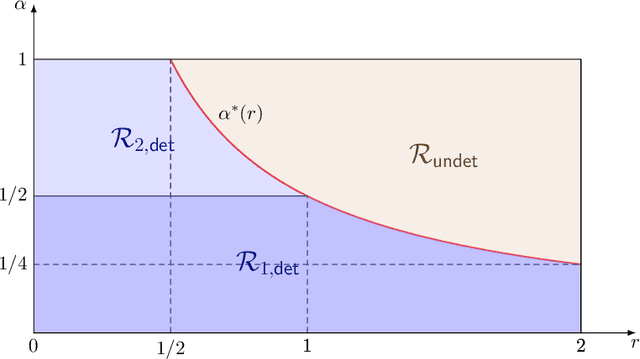
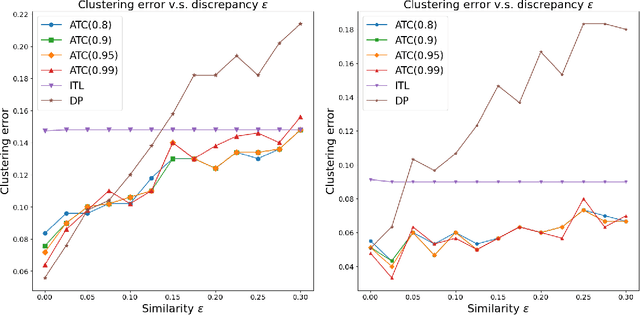
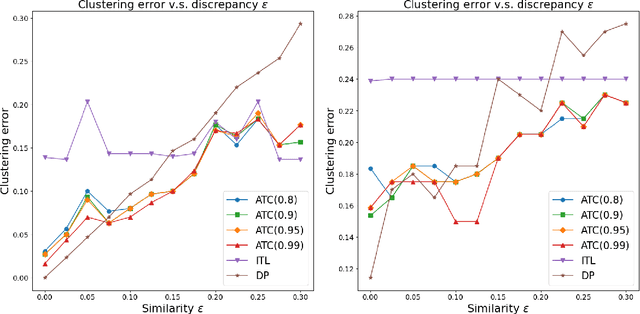
We propose a general transfer learning framework for clustering given a main dataset and an auxiliary one about the same subjects. The two datasets may reflect similar but different latent grouping structures of the subjects. We propose an adaptive transfer clustering (ATC) algorithm that automatically leverages the commonality in the presence of unknown discrepancy, by optimizing an estimated bias-variance decomposition. It applies to a broad class of statistical models including Gaussian mixture models, stochastic block models, and latent class models. A theoretical analysis proves the optimality of ATC under the Gaussian mixture model and explicitly quantifies the benefit of transfer. Extensive simulations and real data experiments confirm our method's effectiveness in various scenarios.

Distribution-Free Predictive Inference under Unknown Temporal Drift

Distribution-free prediction sets play a pivotal role in uncertainty quantification for complex statistical models. Their validity hinges on reliable calibration data, which may not be readily available as real-world environments often undergo unknown changes over time. In this paper, we propose a strategy for choosing an adaptive window and use the data therein to construct prediction sets. The window is selected by optimizing an estimated bias-variance tradeoff. We provide sharp coverage guarantees for our method, showing its adaptivity to the underlying temporal drift. We also illustrate its efficacy through numerical experiments on synthetic and real data.

Credal Wrapper of Model Averaging for Uncertainty Estimation on Out-Of-Distribution Detection

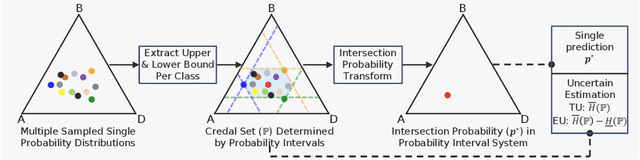
This paper presents an innovative approach, called credal wrapper, to formulating a credal set representation of model averaging for Bayesian neural networks (BNNs) and deep ensembles, capable of improving uncertainty estimation in classification tasks. Given a finite collection of single distributions derived from BNNs or deep ensembles, the proposed approach extracts an upper and a lower probability bound per class, acknowledging the epistemic uncertainty due to the availability of a limited amount of sampled predictive distributions. Such probability intervals over classes can be mapped on a convex set of probabilities (a 'credal set') from which, in turn, a unique prediction can be obtained using a transformation called 'intersection probability transformation'. In this article, we conduct extensive experiments on multiple out-of-distribution (OOD) detection benchmarks, encompassing various dataset pairs (CIFAR10/100 vs SVHN/Tiny-ImageNet, CIFAR10 vs CIFAR10-C, CIFAR100 vs CIFAR100-C and ImageNet vs ImageNet-O) and using different network architectures (such as VGG16, Res18/50, EfficientNet B2, and ViT Base). Compared to BNN and deep ensemble baselines, the proposed credal representation methodology exhibits superior performance in uncertainty estimation and achieves lower expected calibration error on OOD samples.

Model Assessment and Selection under Temporal Distribution Shift

We investigate model assessment and selection in a changing environment, by synthesizing datasets from both the current time period and historical epochs. To tackle unknown and potentially arbitrary temporal distribution shift, we develop an adaptive rolling window approach to estimate the generalization error of a given model. This strategy also facilitates the comparison between any two candidate models by estimating the difference of their generalization errors. We further integrate pairwise comparisons into a single-elimination tournament, achieving near-optimal model selection from a collection of candidates. Theoretical analyses and numerical experiments demonstrate the adaptivity of our proposed methods to the non-stationarity in data.

CreINNs: Credal-Set Interval Neural Networks for Uncertainty Estimation in Classification Tasks

Uncertainty estimation is increasingly attractive for improving the reliability of neural networks. In this work, we present novel credal-set interval neural networks (CreINNs) designed for classification tasks. CreINNs preserve the traditional interval neural network structure, capturing weight uncertainty through deterministic intervals, while forecasting credal sets using the mathematical framework of probability intervals. Experimental validations on an out-of-distribution detection benchmark (CIFAR10 vs SVHN) showcase that CreINNs outperform epistemic uncertainty estimation when compared to variational Bayesian neural networks (BNNs) and deep ensembles (DEs). Furthermore, CreINNs exhibit a notable reduction in computational complexity compared to variational BNNs and demonstrate smaller model sizes than DEs.

A Stability Principle for Learning under Non-Stationarity

We develop a versatile framework for statistical learning in non-stationary environments. In each time period, our approach applies a stability principle to select a look-back window that maximizes the utilization of historical data while keeping the cumulative bias within an acceptable range relative to the stochastic error. Our theory showcases the adaptability of this approach to unknown non-stationarity. The regret bound is minimax optimal up to logarithmic factors when the population losses are strongly convex, or Lipschitz only. At the heart of our analysis lie two novel components: a measure of similarity between functions and a segmentation technique for dividing the non-stationary data sequence into quasi-stationary pieces.

Random-Set Convolutional Neural Network (RS-CNN) for Epistemic Deep Learning

Machine learning is increasingly deployed in safety-critical domains where robustness against adversarial attacks is crucial and erroneous predictions could lead to potentially catastrophic consequences. This highlights the need for learning systems to be equipped with the means to determine a model's confidence in its prediction and the epistemic uncertainty associated with it, 'to know when a model does not know'. In this paper, we propose a novel Random-Set Convolutional Neural Network (RS-CNN) for classification which predicts belief functions rather than probability vectors over the set of classes, using the mathematics of random sets, i.e., distributions over the power set of the sample space. Based on the epistemic deep learning approach, random-set models are capable of representing the 'epistemic' uncertainty induced in machine learning by limited training sets. We estimate epistemic uncertainty by approximating the size of credal sets associated with the predicted belief functions, and experimentally demonstrate how our approach outperforms competing uncertainty-aware approaches in a classical evaluation setting. The performance of RS-CNN is best demonstrated on OOD samples where it manages to capture the true prediction while standard CNNs fail.