A Particle Algorithm for Mean-Field Variational Inference

Variational inference is a fast and scalable alternative to Markov chain Monte Carlo and has been widely applied to posterior inference tasks in statistics and machine learning. A traditional approach for implementing mean-field variational inference (MFVI) is coordinate ascent variational inference (CAVI), which relies crucially on parametric assumptions on complete conditionals. In this paper, we introduce a novel particle-based algorithm for mean-field variational inference, which we term PArticle VI (PAVI). Notably, our algorithm does not rely on parametric assumptions on complete conditionals, and it applies to the nonparametric setting. We provide non-asymptotic finite-particle convergence guarantee for our algorithm. To our knowledge, this is the first end-to-end guarantee for particle-based MFVI.

On Representations of Mean-Field Variational Inference

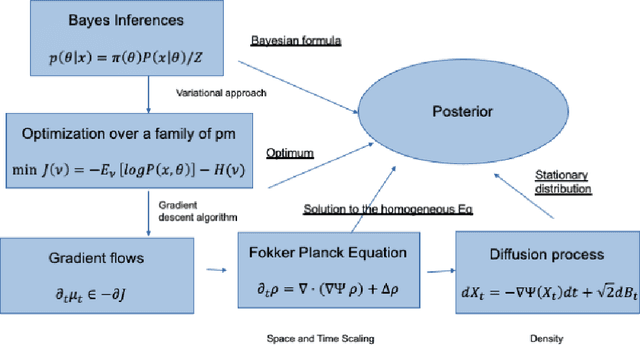
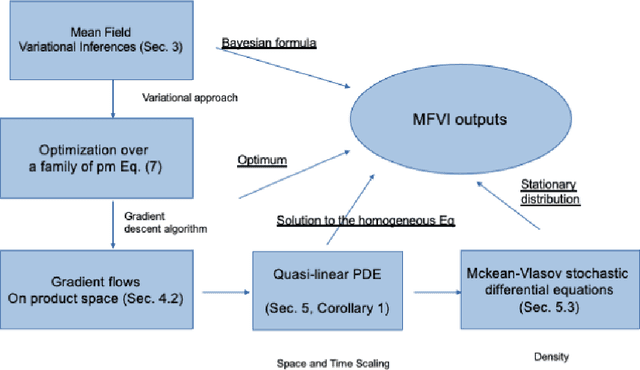
The mean field variational inference (MFVI) formulation restricts the general Bayesian inference problem to the subspace of product measures. We present a framework to analyze MFVI algorithms, which is inspired by a similar development for general variational Bayesian formulations. Our approach enables the MFVI problem to be represented in three different manners: a gradient flow on Wasserstein space, a system of Fokker-Planck-like equations and a diffusion process. Rigorous guarantees are established to show that a time-discretized implementation of the coordinate ascent variational inference algorithm in the product Wasserstein space of measures yields a gradient flow in the limit. A similar result is obtained for their associated densities, with the limit being given by a quasi-linear partial differential equation. A popular class of practical algorithms falls in this framework, which provides tools to establish convergence. We hope this framework could be used to guarantee convergence of algorithms in a variety of approaches, old and new, to solve variational inference problems.