Stackelberg Coupling of Online Representation Learning and Reinforcement Learning

Integrated, end-to-end learning of representations and policies remains a cornerstone of deep reinforcement learning (RL). However, to address the challenge of learning effective features from a sparse reward signal, recent trends have shifted towards adding complex auxiliary objectives or fully decoupling the two processes, often at the cost of increased design complexity. This work proposes an alternative to both decoupling and naive end-to-end learning, arguing that performance can be significantly improved by structuring the interaction between distinct perception and control networks with a principled, game-theoretic dynamic. We formalize this dynamic by introducing the Stackelberg Coupled Representation and Reinforcement Learning (SCORER) framework, which models the interaction between perception and control as a Stackelberg game. The perception network (leader) strategically learns features to benefit the control network (follower), whose own objective is to minimize its Bellman error. We approximate the game's equilibrium with a practical two-timescale algorithm. Applied to standard DQN variants on benchmark tasks, SCORER improves sample efficiency and final performance. Our results show that performance gains can be achieved through principled algorithmic design of the perception-control dynamic, without requiring complex auxiliary objectives or architectures.

SPRIG: Stackelberg Perception-Reinforcement Learning with Internal Game Dynamics

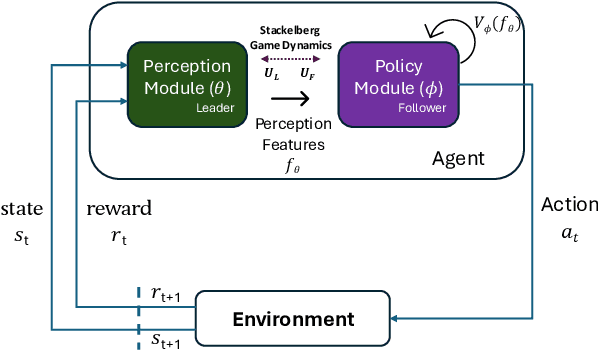
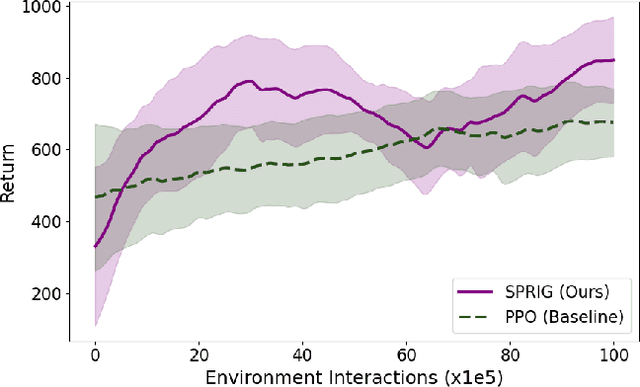
Deep reinforcement learning agents often face challenges to effectively coordinate perception and decision-making components, particularly in environments with high-dimensional sensory inputs where feature relevance varies. This work introduces SPRIG (Stackelberg Perception-Reinforcement learning with Internal Game dynamics), a framework that models the internal perception-policy interaction within a single agent as a cooperative Stackelberg game. In SPRIG, the perception module acts as a leader, strategically processing raw sensory states, while the policy module follows, making decisions based on extracted features. SPRIG provides theoretical guarantees through a modified Bellman operator while preserving the benefits of modern policy optimization. Experimental results on the Atari BeamRider environment demonstrate SPRIG's effectiveness, achieving around 30% higher returns than standard PPO through its game-theoretical balance of feature extraction and decision-making.

Federated Learning for Discrete Optimal Transport with Large Population under Incomplete Information

Optimal transport is a powerful framework for the efficient allocation of resources between sources and targets. However, traditional models often struggle to scale effectively in the presence of large and heterogeneous populations. In this work, we introduce a discrete optimal transport framework designed to handle large-scale, heterogeneous target populations, characterized by type distributions. We address two scenarios: one where the type distribution of targets is known, and one where it is unknown. For the known distribution, we propose a fully distributed algorithm to achieve optimal resource allocation. In the case of unknown distribution, we develop a federated learning-based approach that enables efficient computation of the optimal transport scheme while preserving privacy. Case studies are provided to evaluate the performance of our learning algorithm.

On Convergence of the Alternating Directions SGHMC Algorithm

We study convergence rates of Hamiltonian Monte Carlo (HMC) algorithms with leapfrog integration under mild conditions on stochastic gradient oracle for the target distribution (SGHMC). Our method extends standard HMC by allowing the use of general auxiliary distributions, which is achieved by a novel procedure of Alternating Directions. The convergence analysis is based on the investigations of the Dirichlet forms associated with the underlying Markov chain driving the algorithms. For this purpose, we provide a detailed analysis on the error of the leapfrog integrator for Hamiltonian motions with both the kinetic and potential energy functions in general form. We characterize the explicit dependence of the convergence rates on key parameters such as the problem dimension, functional properties of both the target and auxiliary distributions, and the quality of the oracle.

On Representations of Mean-Field Variational Inference

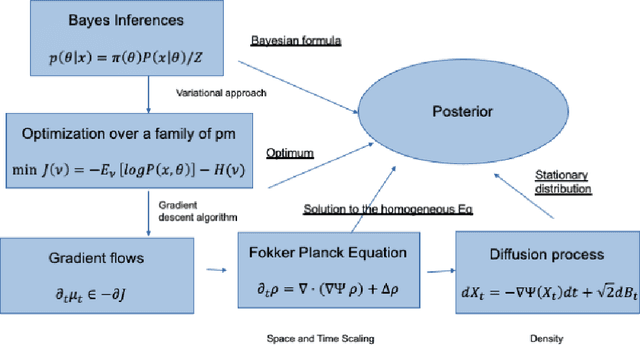
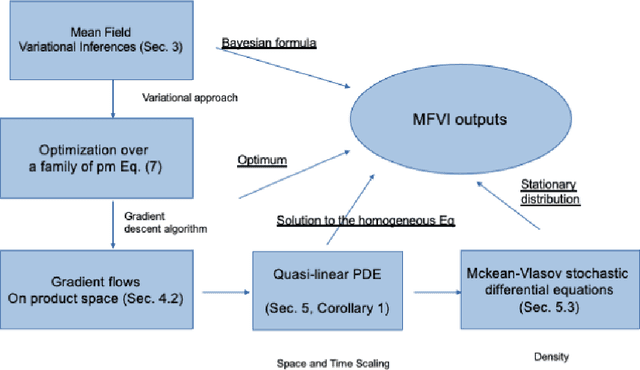
The mean field variational inference (MFVI) formulation restricts the general Bayesian inference problem to the subspace of product measures. We present a framework to analyze MFVI algorithms, which is inspired by a similar development for general variational Bayesian formulations. Our approach enables the MFVI problem to be represented in three different manners: a gradient flow on Wasserstein space, a system of Fokker-Planck-like equations and a diffusion process. Rigorous guarantees are established to show that a time-discretized implementation of the coordinate ascent variational inference algorithm in the product Wasserstein space of measures yields a gradient flow in the limit. A similar result is obtained for their associated densities, with the limit being given by a quasi-linear partial differential equation. A popular class of practical algorithms falls in this framework, which provides tools to establish convergence. We hope this framework could be used to guarantee convergence of algorithms in a variety of approaches, old and new, to solve variational inference problems.

Polynomial convergence of iterations of certain random operators in Hilbert space

We study the convergence of random iterative sequence of a family of operators on infinite dimensional Hilbert spaces, which are inspired by the Stochastic Gradient Descent (SGD) algorithm in the case of the noiseless regression, as studied in [1]. We demonstrate that its polynomial convergence rate depends on the initial state, while the randomness plays a role only in the choice of the best constant factor and we close the gap between the upper and lower bounds.

Hamiltonian Monte Carlo with Asymmetrical Momentum Distributions

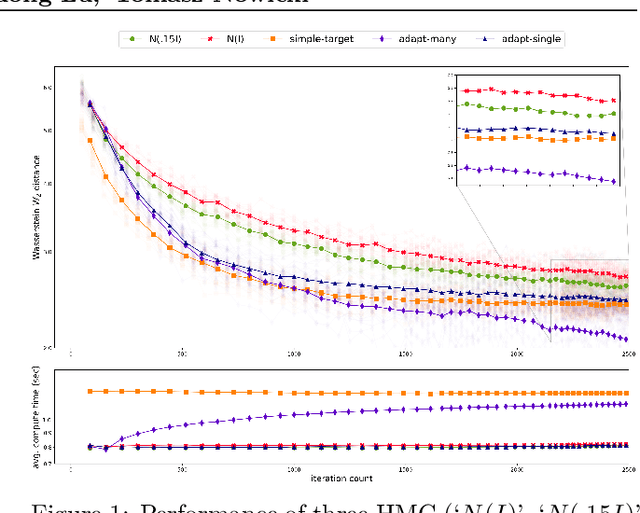
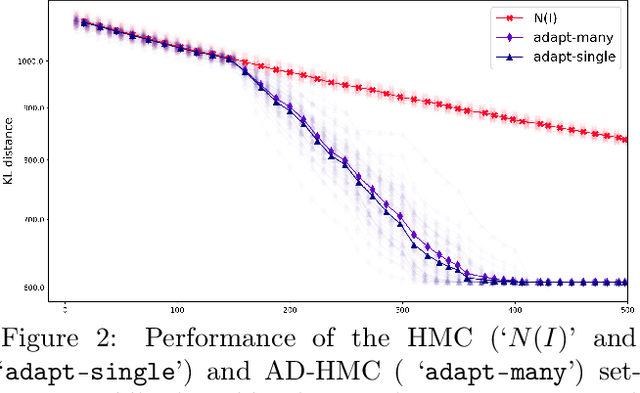
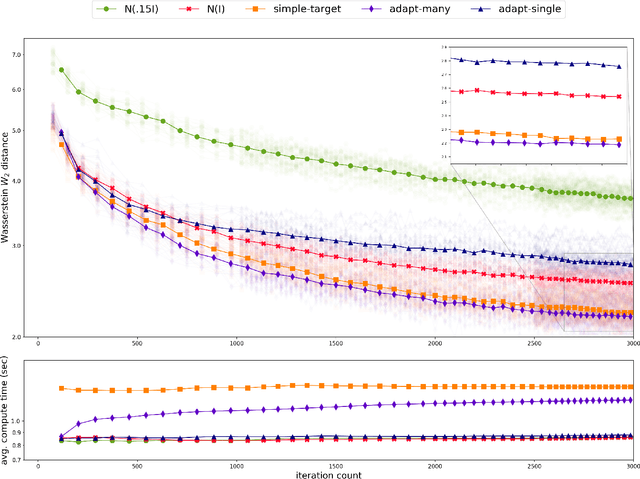
Existing rigorous convergence guarantees for the Hamiltonian Monte Carlo (HMC) algorithm use Gaussian auxiliary momentum variables, which are crucially symmetrically distributed. We present a novel convergence analysis for HMC utilizing new analytic and probabilistic arguments. The convergence is rigorously established under significantly weaker conditions, which among others allow for general auxiliary distributions. In our framework, we show that plain HMC with asymmetrical momentum distributions breaks a key self-adjointness requirement. We propose a modified version that we call the Alternating Direction HMC (AD-HMC). Sufficient conditions are established under which AD-HMC exhibits geometric convergence in Wasserstein distance. Numerical experiments suggest that AD-HMC can show improved performance over HMC with Gaussian auxiliaries.

HMC, an Algorithms in Data Mining, the Functional Analysis approach

The main purpose of this paper is to facilitate the communication between the Analytic, Probabilistic and Algorithmic communities. We present a proof of convergence of the Hamiltonian (Hybrid) Monte Carlo algorithm from the point of view of the Dynamical Systems, where the evolving objects are densities of probability distributions and the tool are derived from the Functional Analysis.

HMC, an example of Functional Analysis applied to Algorithms in Data Mining. The convergence in $L^p$

We present a proof of convergence of the Hamiltonian Monte Carlo algorithm in terms of Functional Analysis. We represent the algorithm as an operator on the density functions, and prove the convergence of iterations of this operator in $L^p$, for $1<p<\infty$, and strong convergence for $2\le p<\infty$.

A Control-Model-Based Approach for Reinforcement Learning

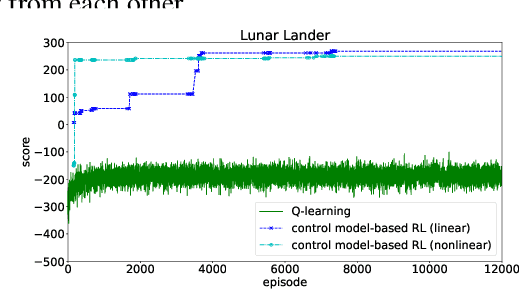
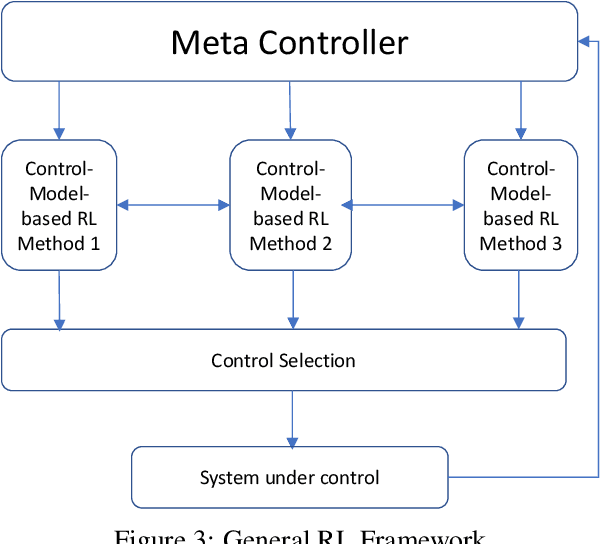
We consider a new form of model-based reinforcement learning methods that directly learns the optimal control parameters, instead of learning the underlying dynamical system. This includes a form of exploration and exploitation in learning and applying the optimal control parameters over time. This also includes a general framework that manages a collection of such control-model-based reinforcement learning methods running in parallel and that selects the best decision from among these parallel methods with the different methods interactively learning together. We derive theoretical results for the optimal control of linear and nonlinear instances of the new control-model-based reinforcement learning methods. Our empirical results demonstrate and quantify the significant benefits of our approach.