Obtaining Explainable Classification Models using Distributionally Robust Optimization

Model explainability is crucial for human users to be able to interpret how a proposed classifier assigns labels to data based on its feature values. We study generalized linear models constructed using sets of feature value rules, which can capture nonlinear dependencies and interactions. An inherent trade-off exists between rule set sparsity and its prediction accuracy. It is computationally expensive to find the right choice of sparsity -- e.g., via cross-validation -- with existing methods. We propose a new formulation to learn an ensemble of rule sets that simultaneously addresses these competing factors. Good generalization is ensured while keeping computational costs low by utilizing distributionally robust optimization. The formulation utilizes column generation to efficiently search the space of rule sets and constructs a sparse ensemble of rule sets, in contrast with techniques like random forests or boosting and their variants. We present theoretical results that motivate and justify the use of our distributionally robust formulation. Extensive numerical experiments establish that our method improves over competing methods -- on a large set of publicly available binary classification problem instances -- with respect to one or more of the following metrics: generalization quality, computational cost, and explainability.

On Representations of Mean-Field Variational Inference

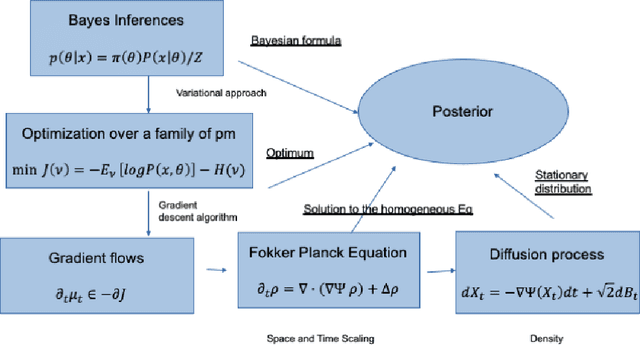
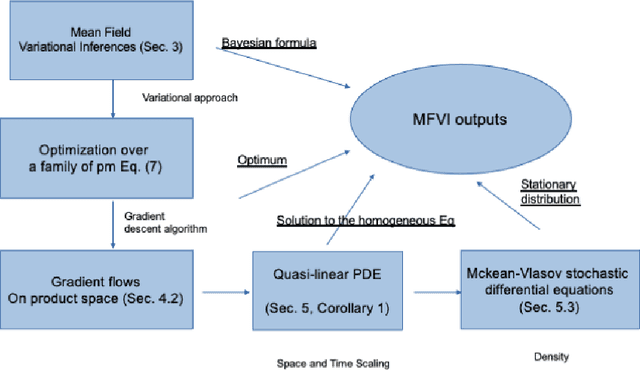
The mean field variational inference (MFVI) formulation restricts the general Bayesian inference problem to the subspace of product measures. We present a framework to analyze MFVI algorithms, which is inspired by a similar development for general variational Bayesian formulations. Our approach enables the MFVI problem to be represented in three different manners: a gradient flow on Wasserstein space, a system of Fokker-Planck-like equations and a diffusion process. Rigorous guarantees are established to show that a time-discretized implementation of the coordinate ascent variational inference algorithm in the product Wasserstein space of measures yields a gradient flow in the limit. A similar result is obtained for their associated densities, with the limit being given by a quasi-linear partial differential equation. A popular class of practical algorithms falls in this framework, which provides tools to establish convergence. We hope this framework could be used to guarantee convergence of algorithms in a variety of approaches, old and new, to solve variational inference problems.

A Class of Geometric Structures in Transfer Learning: Minimax Bounds and Optimality

We study the problem of transfer learning, observing that previous efforts to understand its information-theoretic limits do not fully exploit the geometric structure of the source and target domains. In contrast, our study first illustrates the benefits of incorporating a natural geometric structure within a linear regression model, which corresponds to the generalized eigenvalue problem formed by the Gram matrices of both domains. We next establish a finite-sample minimax lower bound, propose a refined model interpolation estimator that enjoys a matching upper bound, and then extend our framework to multiple source domains and generalized linear models. Surprisingly, as long as information is available on the distance between the source and target parameters, negative-transfer does not occur. Simulation studies show that our proposed interpolation estimator outperforms state-of-the-art transfer learning methods in both moderate- and high-dimensional settings.

Polynomial convergence of iterations of certain random operators in Hilbert space

We study the convergence of random iterative sequence of a family of operators on infinite dimensional Hilbert spaces, which are inspired by the Stochastic Gradient Descent (SGD) algorithm in the case of the noiseless regression, as studied in [1]. We demonstrate that its polynomial convergence rate depends on the initial state, while the randomness plays a role only in the choice of the best constant factor and we close the gap between the upper and lower bounds.

Hamiltonian Monte Carlo with Asymmetrical Momentum Distributions

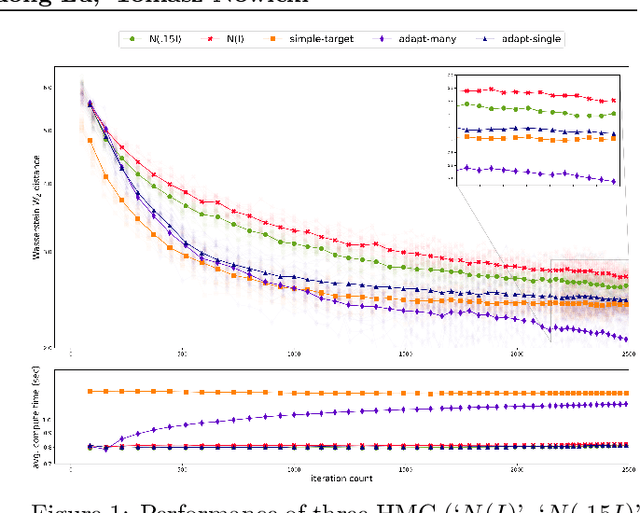
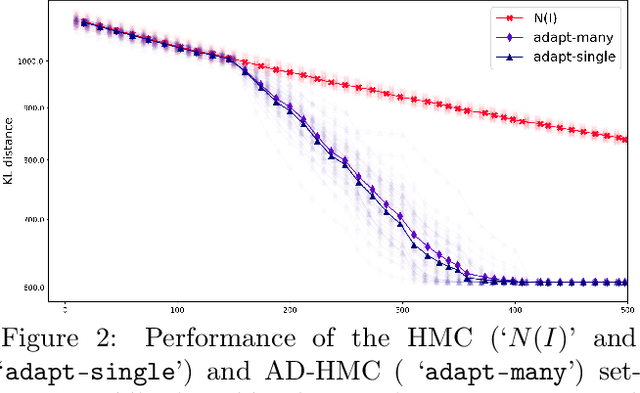
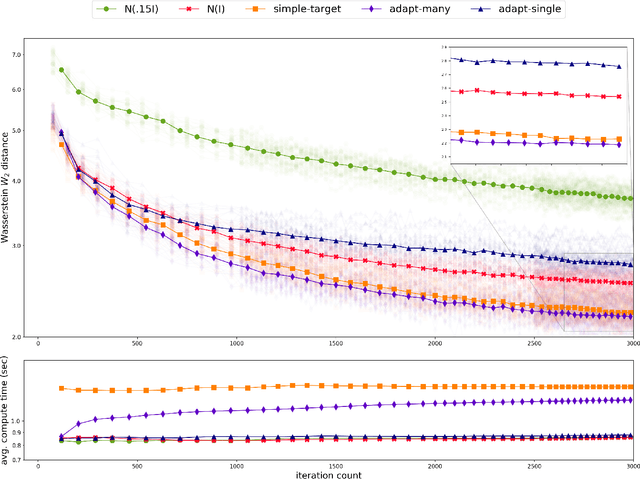
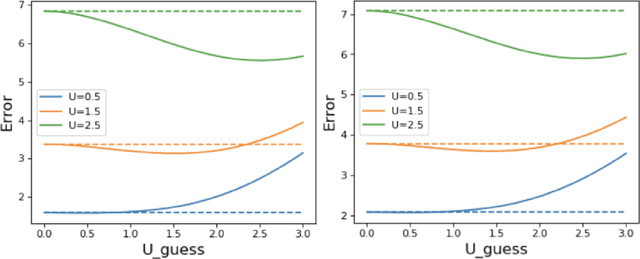
Existing rigorous convergence guarantees for the Hamiltonian Monte Carlo (HMC) algorithm use Gaussian auxiliary momentum variables, which are crucially symmetrically distributed. We present a novel convergence analysis for HMC utilizing new analytic and probabilistic arguments. The convergence is rigorously established under significantly weaker conditions, which among others allow for general auxiliary distributions. In our framework, we show that plain HMC with asymmetrical momentum distributions breaks a key self-adjointness requirement. We propose a modified version that we call the Alternating Direction HMC (AD-HMC). Sufficient conditions are established under which AD-HMC exhibits geometric convergence in Wasserstein distance. Numerical experiments suggest that AD-HMC can show improved performance over HMC with Gaussian auxiliaries.

EventGraD: Event-Triggered Communication in Parallel Machine Learning

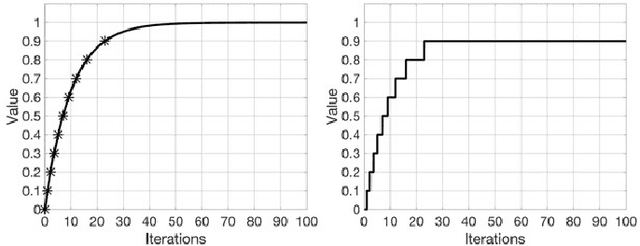
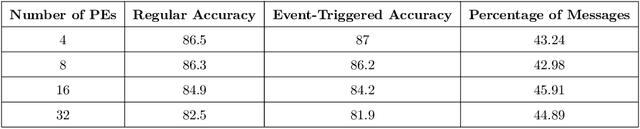
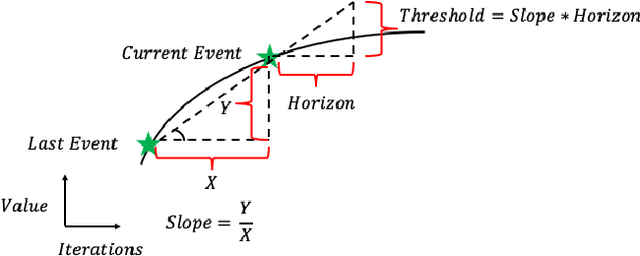
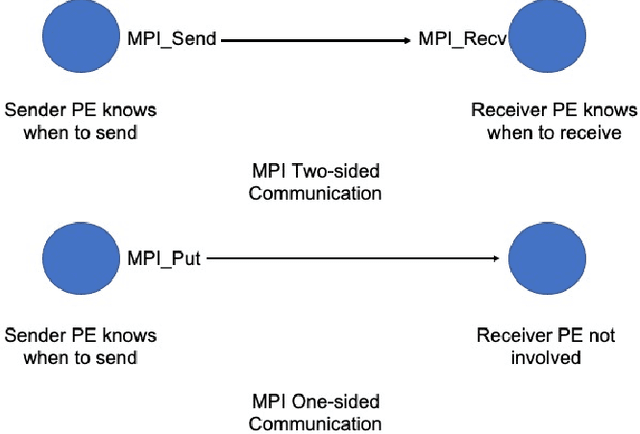
Communication in parallel systems imposes significant overhead which often turns out to be a bottleneck in parallel machine learning. To relieve some of this overhead, in this paper, we present EventGraD - an algorithm with event-triggered communication for stochastic gradient descent in parallel machine learning. The main idea of this algorithm is to modify the requirement of communication at every iteration in standard implementations of stochastic gradient descent in parallel machine learning to communicating only when necessary at certain iterations. We provide theoretical analysis of convergence of our proposed algorithm. We also implement the proposed algorithm for data-parallel training of a popular residual neural network used for training the CIFAR-10 dataset and show that EventGraD can reduce the communication load by up to 60% while retaining the same level of accuracy.

HMC, an Algorithms in Data Mining, the Functional Analysis approach

The main purpose of this paper is to facilitate the communication between the Analytic, Probabilistic and Algorithmic communities. We present a proof of convergence of the Hamiltonian (Hybrid) Monte Carlo algorithm from the point of view of the Dynamical Systems, where the evolving objects are densities of probability distributions and the tool are derived from the Functional Analysis.

HMC, an example of Functional Analysis applied to Algorithms in Data Mining. The convergence in $L^p$

We present a proof of convergence of the Hamiltonian Monte Carlo algorithm in terms of Functional Analysis. We represent the algorithm as an operator on the density functions, and prove the convergence of iterations of this operator in $L^p$, for $1<p<\infty$, and strong convergence for $2\le p<\infty$.

Unbiased Gradient Estimation for Distributionally Robust Learning

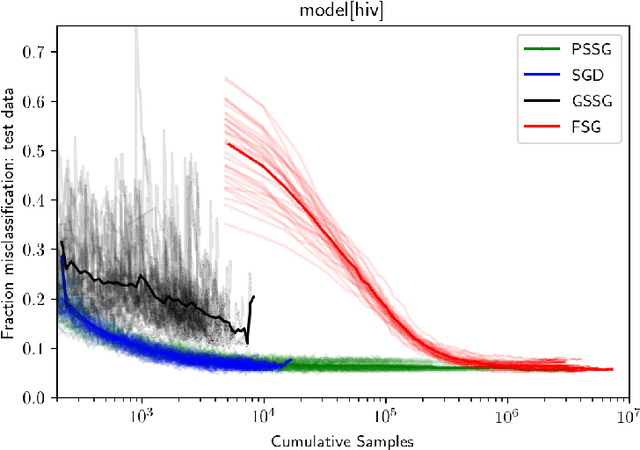
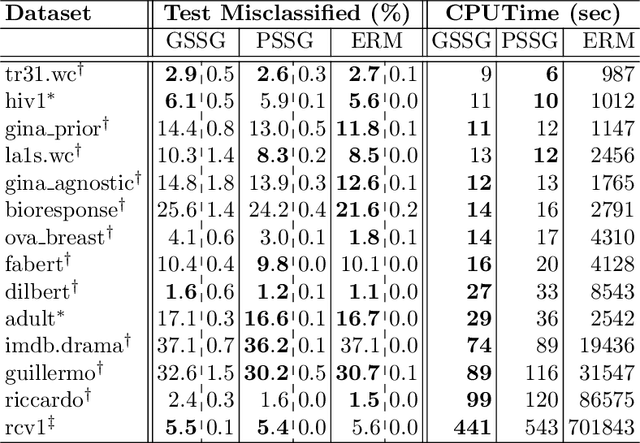
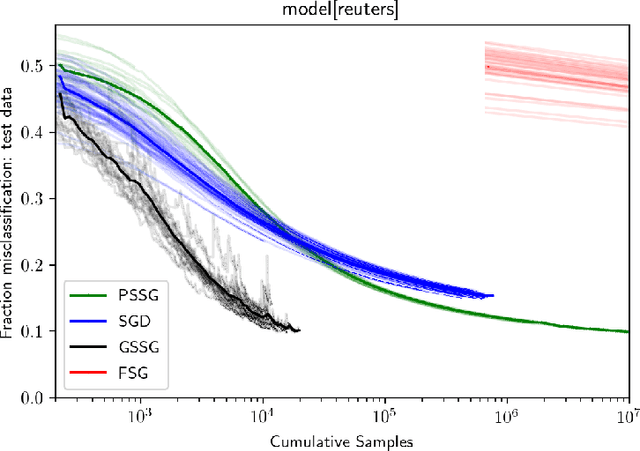
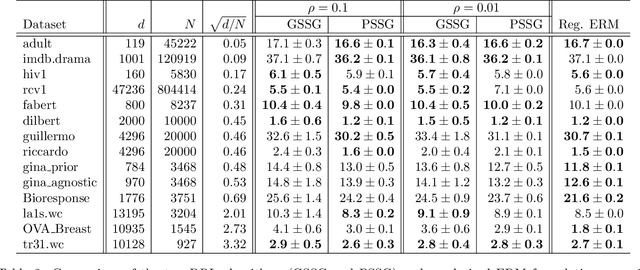
Seeking to improve model generalization, we consider a new approach based on distributionally robust learning (DRL) that applies stochastic gradient descent to the outer minimization problem. Our algorithm efficiently estimates the gradient of the inner maximization problem through multi-level Monte Carlo randomization. Leveraging theoretical results that shed light on why standard gradient estimators fail, we establish the optimal parameterization of the gradient estimators of our approach that balances a fundamental tradeoff between computation time and statistical variance. Numerical experiments demonstrate that our DRL approach yields significant benefits over previous work.

Efficient Stochastic Gradient Descent for Distributionally Robust Learning

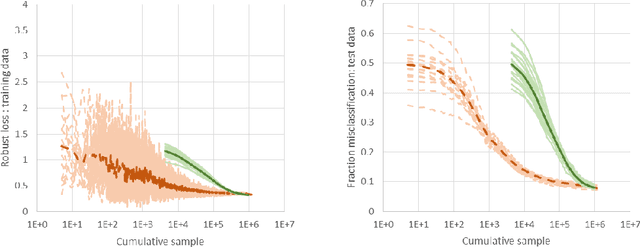
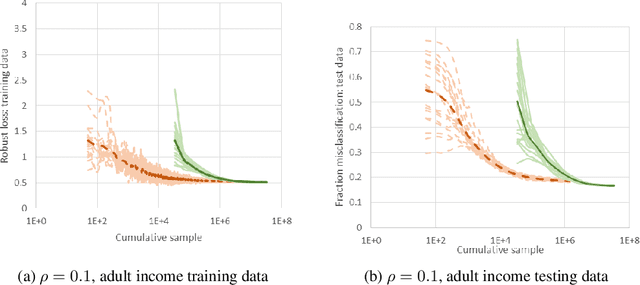
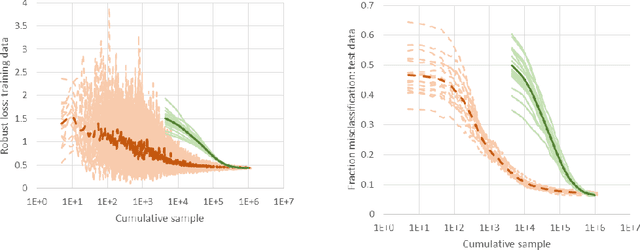
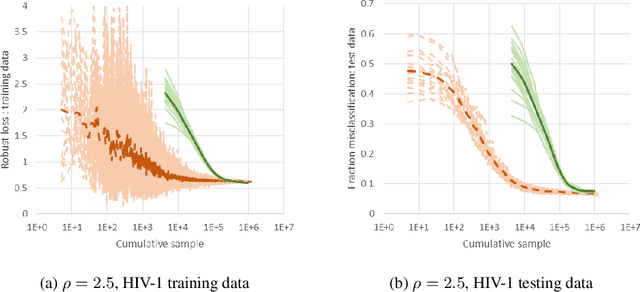
We consider a new stochastic gradient descent algorithm for efficiently solving general min-max optimization problems that arise naturally in distributionally robust learning. By focusing on the entire dataset, current approaches do not scale well. We address this issue by initially focusing on a subset of the data and progressively increasing this support to statistically cover the entire dataset.