Unbiased Gradient Estimation for Distributionally Robust Learning
Paper and Code
Dec 22, 2020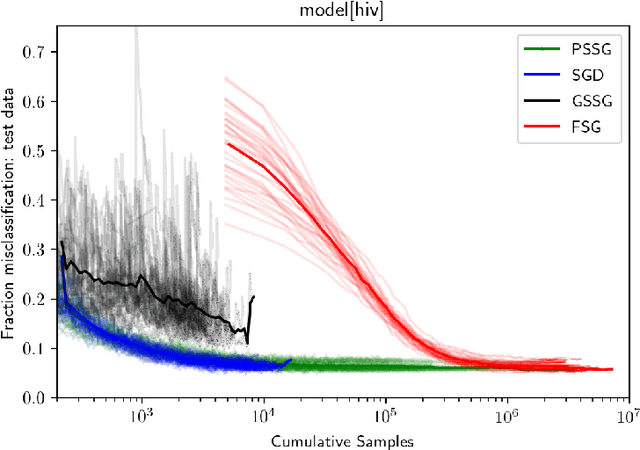
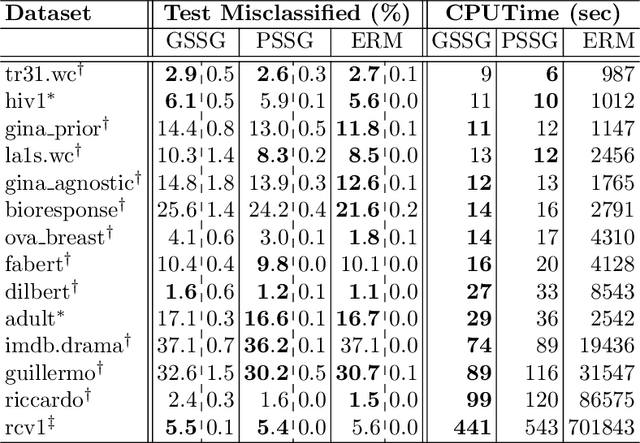
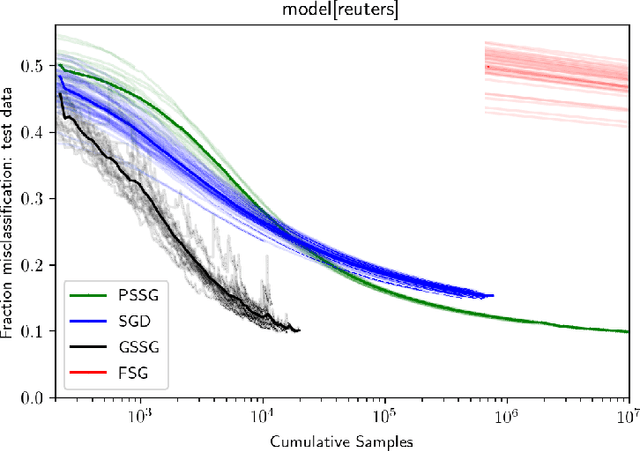
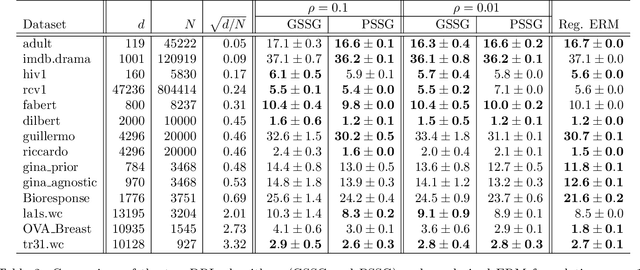
Seeking to improve model generalization, we consider a new approach based on distributionally robust learning (DRL) that applies stochastic gradient descent to the outer minimization problem. Our algorithm efficiently estimates the gradient of the inner maximization problem through multi-level Monte Carlo randomization. Leveraging theoretical results that shed light on why standard gradient estimators fail, we establish the optimal parameterization of the gradient estimators of our approach that balances a fundamental tradeoff between computation time and statistical variance. Numerical experiments demonstrate that our DRL approach yields significant benefits over previous work.
* ICML 2020, AISTATS 2021 submission
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge