Statsformer: Validated Ensemble Learning with LLM-Derived Semantic Priors

We introduce Statsformer, a principled framework for integrating large language model (LLM)-derived knowledge into supervised statistical learning. Existing approaches are limited in adaptability and scope: they either inject LLM guidance as an unvalidated heuristic, which is sensitive to LLM hallucination, or embed semantic information within a single fixed learner. Statsformer overcomes both limitations through a guardrailed ensemble architecture. We embed LLM-derived feature priors within an ensemble of linear and nonlinear learners, adaptively calibrating their influence via cross-validation. This design yields a flexible system with an oracle-style guarantee that it performs no worse than any convex combination of its in-library base learners, up to statistical error. Empirically, informative priors yield consistent performance improvements, while uninformative or misspecified LLM guidance is automatically downweighted, mitigating the impact of hallucinations across a diverse range of prediction tasks.

FutureX-Pro: Extending Future Prediction to High-Value Vertical Domains

Building upon FutureX, which established a live benchmark for general-purpose future prediction, this report introduces FutureX-Pro, including FutureX-Finance, FutureX-Retail, FutureX-PublicHealth, FutureX-NaturalDisaster, and FutureX-Search. These together form a specialized framework extending agentic future prediction to high-value vertical domains. While generalist agents demonstrate proficiency in open-domain search, their reliability in capital-intensive and safety-critical sectors remains under-explored. FutureX-Pro targets four economically and socially pivotal verticals: Finance, Retail, Public Health, and Natural Disaster. We benchmark agentic Large Language Models (LLMs) on entry-level yet foundational prediction tasks -- ranging from forecasting market indicators and supply chain demands to tracking epidemic trends and natural disasters. By adapting the contamination-free, live-evaluation pipeline of FutureX, we assess whether current State-of-the-Art (SOTA) agentic LLMs possess the domain grounding necessary for industrial deployment. Our findings reveal the performance gap between generalist reasoning and the precision required for high-value vertical applications.

Robust equilibria in continuous games: From strategic to dynamic robustness

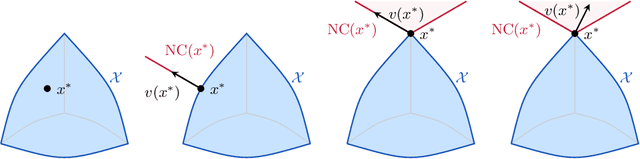
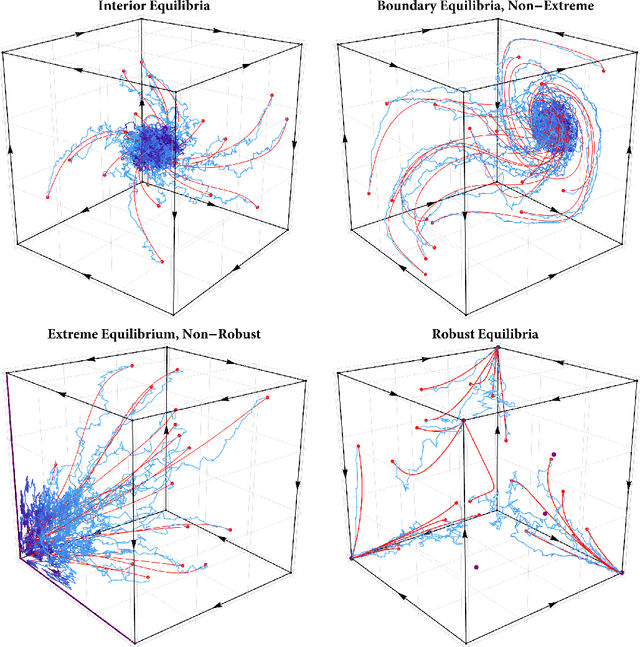
In this paper, we examine the robustness of Nash equilibria in continuous games, under both strategic and dynamic uncertainty. Starting with the former, we introduce the notion of a robust equilibrium as those equilibria that remain invariant to small -- but otherwise arbitrary -- perturbations to the game's payoff structure, and we provide a crisp geometric characterization thereof. Subsequently, we turn to the question of dynamic robustness, and we examine which equilibria may arise as stable limit points of the dynamics of "follow the regularized leader" (FTRL) in the presence of randomness and uncertainty. Despite their very distinct origins, we establish a structural correspondence between these two notions of robustness: strategic robustness implies dynamic robustness, and, conversely, the requirement of strategic robustness cannot be relaxed if dynamic robustness is to be maintained. Finally, we examine the rate of convergence to robust equilibria as a function of the underlying regularizer, and we show that entropically regularized learning converges at a geometric rate in games with affinely constrained action spaces.

Multi-agent learning under uncertainty: Recurrence vs. concentration

In this paper, we examine the convergence landscape of multi-agent learning under uncertainty. Specifically, we analyze two stochastic models of regularized learning in continuous games -- one in continuous and one in discrete time with the aim of characterizing the long-run behavior of the induced sequence of play. In stark contrast to deterministic, full-information models of learning (or models with a vanishing learning rate), we show that the resulting dynamics do not converge in general. In lieu of this, we ask instead which actions are played more often in the long run, and by how much. We show that, in strongly monotone games, the dynamics of regularized learning may wander away from equilibrium infinitely often, but they always return to its vicinity in finite time (which we estimate), and their long-run distribution is sharply concentrated around a neighborhood thereof. We quantify the degree of this concentration, and we show that these favorable properties may all break down if the underlying game is not strongly monotone -- underscoring in this way the limits of regularized learning in the presence of persistent randomness and uncertainty.

Duality and Policy Evaluation in Distributionally Robust Bayesian Diffusion Control

We consider a Bayesian diffusion control problem of expected terminal utility maximization. The controller imposes a prior distribution on the unknown drift of an underlying diffusion. The Bayesian optimal control, tracking the posterior distribution of the unknown drift, can be characterized explicitly. However, in practice, the prior will generally be incorrectly specified, and the degree of model misspecification can have a significant impact on policy performance. To mitigate this and reduce overpessimism, we introduce a distributionally robust Bayesian control (DRBC) formulation in which the controller plays a game against an adversary who selects a prior in divergence neighborhood of a baseline prior. The adversarial approach has been studied in economics and efficient algorithms have been proposed in static optimization settings. We develop a strong duality result for our DRBC formulation. Combining these results together with tools from stochastic analysis, we are able to derive a loss that can be efficiently trained (as we demonstrate in our numerical experiments) using a suitable neural network architecture. As a result, we obtain an effective algorithm for computing the DRBC optimal strategy. The methodology for computing the DRBC optimal strategy is greatly simplified, as we show, in the important case in which the adversary chooses a prior from a Kullback-Leibler distributional uncertainty set.

DRO: A Python Library for Distributionally Robust Optimization in Machine Learning

We introduce dro, an open-source Python library for distributionally robust optimization (DRO) for regression and classification problems. The library implements 14 DRO formulations and 9 backbone models, enabling 79 distinct DRO methods. Furthermore, dro is compatible with both scikit-learn and PyTorch. Through vectorization and optimization approximation techniques, dro reduces runtime by 10x to over 1000x compared to baseline implementations on large-scale datasets. Comprehensive documentation is available at https://python-dro.org.

Wasserstein Distributionally Robust Regret Optimization

Distributionally Robust Optimization (DRO) is a popular framework for decision-making under uncertainty, but its adversarial nature can lead to overly conservative solutions. To address this, we study ex-ante Distributionally Robust Regret Optimization (DRRO), focusing on Wasserstein-based ambiguity sets which are popular due to their links to regularization and machine learning. We provide a systematic analysis of Wasserstein DRRO, paralleling known results for Wasserstein DRO. Under smoothness and regularity conditions, we show that Wasserstein DRRO coincides with Empirical Risk Minimization (ERM) up to first-order terms, and exactly so in convex quadratic settings. We revisit the Wasserstein DRRO newsvendor problem, where the loss is the maximum of two linear functions of demand and decision. Extending [25], we show that the regret can be computed by maximizing two one-dimensional concave functions. For more general loss functions involving the maximum of multiple linear terms in multivariate random variables and decision vectors, we prove that computing the regret and thus also the DRRO policy is NP-hard. We then propose a convex relaxation for these more general Wasserstein DRRO problems and demonstrate its strong empirical performance. Finally, we provide an upper bound on the optimality gap of our relaxation and show it improves over recent alternatives.

Learning an Optimal Assortment Policy under Observational Data

We study the fundamental problem of offline assortment optimization under the Multinomial Logit (MNL) model, where sellers must determine the optimal subset of the products to offer based solely on historical customer choice data. While most existing approaches to learning-based assortment optimization focus on the online learning of the optimal assortment through repeated interactions with customers, such exploration can be costly or even impractical in many real-world settings. In this paper, we consider the offline learning paradigm and investigate the minimal data requirements for efficient offline assortment optimization. To this end, we introduce Pessimistic Rank-Breaking (PRB), an algorithm that combines rank-breaking with pessimistic estimation. We prove that PRB is nearly minimax optimal by establishing the tight suboptimality upper bound and a nearly matching lower bound. This further shows that "optimal item coverage" - where each item in the optimal assortment appears sufficiently often in the historical data - is both sufficient and necessary for efficient offline learning. This significantly relaxes the previous requirement of observing the complete optimal assortment in the data. Our results provide fundamental insights into the data requirements for offline assortment optimization under the MNL model.

Non-linear Quantum Monte Carlo

The mean of a random variable can be understood as a $\textit{linear}$ functional on the space of probability distributions. Quantum computing is known to provide a quadratic speedup over classical Monte Carlo methods for mean estimation. In this paper, we investigate whether a similar quadratic speedup is achievable for estimating $\textit{non-linear}$ functionals of probability distributions. We propose a quantum-inside-quantum Monte Carlo algorithm that achieves such a speedup for a broad class of non-linear estimation problems, including nested conditional expectations and stochastic optimization. Our algorithm improves upon the direct application of the quantum multilevel Monte Carlo algorithm introduced by An et al.. The existing lower bound indicates that our algorithm is optimal up polylogarithmic factors. A key innovation of our approach is a new sequence of multilevel Monte Carlo approximations specifically designed for quantum computing, which is central to the algorithm's improved performance.

Limit Theorems for Stochastic Gradient Descent with Infinite Variance

Stochastic gradient descent is a classic algorithm that has gained great popularity especially in the last decades as the most common approach for training models in machine learning. While the algorithm has been well-studied when stochastic gradients are assumed to have a finite variance, there is significantly less research addressing its theoretical properties in the case of infinite variance gradients. In this paper, we establish the asymptotic behavior of stochastic gradient descent in the context of infinite variance stochastic gradients, assuming that the stochastic gradient is regular varying with index $\alpha\in(1,2)$. The closest result in this context was established in 1969 , in the one-dimensional case and assuming that stochastic gradients belong to a more restrictive class of distributions. We extend it to the multidimensional case, covering a broader class of infinite variance distributions. As we show, the asymptotic distribution of the stochastic gradient descent algorithm can be characterized as the stationary distribution of a suitably defined Ornstein-Uhlenbeck process driven by an appropriate stable L\'evy process. Additionally, we explore the applications of these results in linear regression and logistic regression models.