CCS: Controllable and Constrained Sampling with Diffusion Models via Initial Noise Perturbation

Diffusion models have emerged as powerful tools for generative tasks, producing high-quality outputs across diverse domains. However, how the generated data responds to the initial noise perturbation in diffusion models remains under-explored, which hinders understanding the controllability of the sampling process. In this work, we first observe an interesting phenomenon: the relationship between the change of generation outputs and the scale of initial noise perturbation is highly linear through the diffusion ODE sampling. Then we provide both theoretical and empirical study to justify this linearity property of this input-output (noise-generation data) relationship. Inspired by these new insights, we propose a novel Controllable and Constrained Sampling method (CCS) together with a new controller algorithm for diffusion models to sample with desired statistical properties while preserving good sample quality. We perform extensive experiments to compare our proposed sampling approach with other methods on both sampling controllability and sampled data quality. Results show that our CCS method achieves more precisely controlled sampling while maintaining superior sample quality and diversity.

Non-linear Quantum Monte Carlo

The mean of a random variable can be understood as a $\textit{linear}$ functional on the space of probability distributions. Quantum computing is known to provide a quadratic speedup over classical Monte Carlo methods for mean estimation. In this paper, we investigate whether a similar quadratic speedup is achievable for estimating $\textit{non-linear}$ functionals of probability distributions. We propose a quantum-inside-quantum Monte Carlo algorithm that achieves such a speedup for a broad class of non-linear estimation problems, including nested conditional expectations and stochastic optimization. Our algorithm improves upon the direct application of the quantum multilevel Monte Carlo algorithm introduced by An et al.. The existing lower bound indicates that our algorithm is optimal up polylogarithmic factors. A key innovation of our approach is a new sequence of multilevel Monte Carlo approximations specifically designed for quantum computing, which is central to the algorithm's improved performance.

A phase transition in sampling from Restricted Boltzmann Machines

Restricted Boltzmann Machines are a class of undirected graphical models that play a key role in deep learning and unsupervised learning. In this study, we prove a phase transition phenomenon in the mixing time of the Gibbs sampler for a one-parameter Restricted Boltzmann Machine. Specifically, the mixing time varies logarithmically, polynomially, and exponentially with the number of vertices depending on whether the parameter $c$ is above, equal to, or below a critical value $c_\star\approx-5.87$. A key insight from our analysis is the link between the Gibbs sampler and a dynamical system, which we utilize to quantify the former based on the behavior of the latter. To study the critical case $c= c_\star$, we develop a new isoperimetric inequality for the sampler's stationary distribution by showing that the distribution is nearly log-concave.

Markov chain Monte Carlo without evaluating the target: an auxiliary variable approach

In sampling tasks, it is common for target distributions to be known up to a normalizing constant. However, in many situations, evaluating even the unnormalized distribution can be costly or infeasible. This issue arises in scenarios such as sampling from the Bayesian posterior for tall datasets and the `doubly-intractable' distributions. In this paper, we begin by observing that seemingly different Markov chain Monte Carlo (MCMC) algorithms, such as the exchange algorithm, PoissonMH, and TunaMH, can be unified under a simple common procedure. We then extend this procedure into a novel framework that allows the use of auxiliary variables in both the proposal and acceptance-rejection steps. We develop the theory of the new framework, applying it to existing algorithms to simplify and extend their results. Several new algorithms emerge from this framework, with improved performance demonstrated on both synthetic and real datasets.

Differentially Private Range Queries with Correlated Input Perturbation

This work proposes a class of locally differentially private mechanisms for linear queries, in particular range queries, that leverages correlated input perturbation to simultaneously achieve unbiasedness, consistency, statistical transparency, and control over utility requirements in terms of accuracy targets expressed either in certain query margins or as implied by the hierarchical database structure. The proposed Cascade Sampling algorithm instantiates the mechanism exactly and efficiently. Our bounds show that we obtain near-optimal utility while being empirically competitive against output perturbation methods.

Optimal randomized multilevel Monte Carlo for repeatedly nested expectations

The estimation of repeatedly nested expectations is a challenging problem that arises in many real-world systems. However, existing methods generally suffer from high computational costs when the number of nestings becomes large. Fix any non-negative integer $D$ for the total number of nestings. Standard Monte Carlo methods typically cost at least $\mathcal{O}(\varepsilon^{-(2+D)})$ and sometimes $\mathcal{O}(\varepsilon^{-2(1+D)})$ to obtain an estimator up to $\varepsilon$-error. More advanced methods, such as multilevel Monte Carlo, currently only exist for $D = 1$. In this paper, we propose a novel Monte Carlo estimator called $\mathsf{READ}$, which stands for "Recursive Estimator for Arbitrary Depth.'' Our estimator has an optimal computational cost of $\mathcal{O}(\varepsilon^{-2})$ for every fixed $D$ under suitable assumptions, and a nearly optimal computational cost of $\mathcal{O}(\varepsilon^{-2(1 + \delta)})$ for any $0 < \delta < \frac12$ under much more general assumptions. Our estimator is also unbiased, which makes it easy to parallelize. The key ingredients in our construction are an observation of the problem's recursive structure and the recursive use of the randomized multilevel Monte Carlo method.

On the Theoretical Properties of Exchange Algorithm

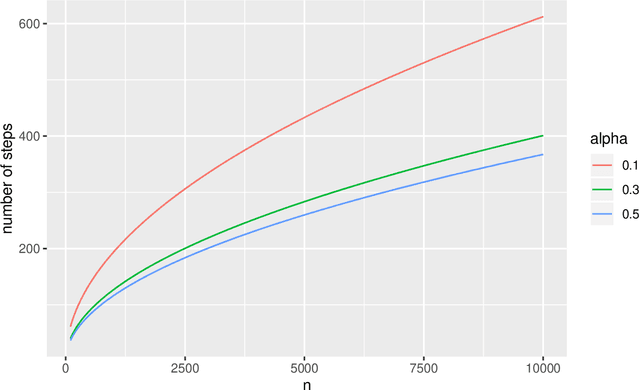
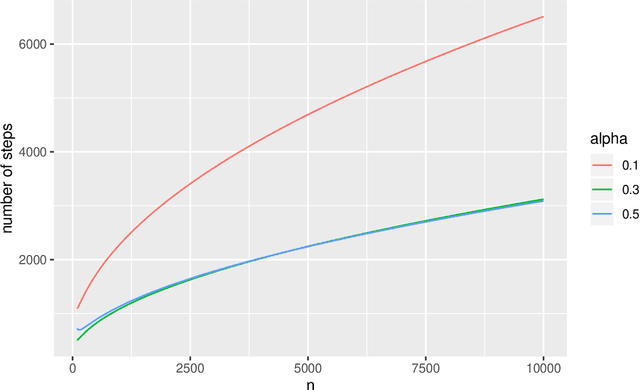
Exchange algorithm is one of the most popular extensions of Metropolis-Hastings algorithm to sample from doubly-intractable distributions. However, theoretical exploration of exchange algorithm is very limited. For example, natural questions like `Does exchange algorithm converge at a geometric rate?' or `Does the exchange algorithm admit a Central Limit Theorem?' have not been answered. In this paper, we study the theoretical properties of exchange algorithm, in terms of asymptotic variance and convergence speed. We compare the exchange algorithm with the original Metropolis-Hastings algorithm and provide both necessary and sufficient conditions for geometric ergodicity of the exchange algorithm, which can be applied to various practical applications such as exponential random graph models and Ising models. A central limit theorem for the exchange algorithm is also established. Meanwhile, a concrete example, involving the Beta-Binomial model, is treated in detail with sharp convergence rates. Our results justify the theoretical usefulness of the exchange algorithm.

Modeling treatment events in disease progression

Ability to quantify and predict progression of a disease is fundamental for selecting an appropriate treatment. Many clinical metrics cannot be acquired frequently either because of their cost (e.g. MRI, gait analysis) or because they are inconvenient or harmful to a patient (e.g. biopsy, x-ray). In such scenarios, in order to estimate individual trajectories of disease progression, it is advantageous to leverage similarities between patients, i.e. the covariance of trajectories, and find a latent representation of progression. Most of existing methods for estimating trajectories do not account for events in-between observations, what dramatically decreases their adequacy for clinical practice. In this study, we develop a machine learning framework named Coordinatewise-Soft-Impute (CSI) for analyzing disease progression from sparse observations in the presence of confounding events. CSI is guaranteed to converge to the global minimum of the corresponding optimization problem. Experimental results also demonstrates the effectiveness of CSI using both simulated and real dataset.

A Multi-armed Bandit MCMC, with applications in sampling from doubly intractable posterior

Markov chain Monte Carlo (MCMC) algorithms are widely used to sample from complicated distributions, especially to sample from the posterior distribution in Bayesian inference. However, MCMC is not directly applicable when facing the doubly intractable problem. In this paper, we discussed and compared two existing solutions -- Pseudo-marginal Monte Carlo and Exchange Algorithm. This paper also proposes a novel algorithm: Multi-armed Bandit MCMC (MABMC), which chooses between two (or more) randomized acceptance ratios in each step. MABMC could be applied directly to incorporate Pseudo-marginal Monte Carlo and Exchange algorithm, with higher average acceptance probability.