Rotated Mean-Field Variational Inference and Iterative Gaussianization

We propose to perform mean-field variational inference (MFVI) in a rotated coordinate system that reduces correlations between variables. The rotation is determined by principal component analysis (PCA) of a cross-covariance matrix involving the target's score function. Compared with standard MFVI along the original axes, MFVI in this rotated system often yields substantially more accurate approximations with negligible additional cost. MFVI in a rotated coordinate system defines a rotation and a coordinatewise map that together move the target closer to Gaussian. Iterating this procedure yields a sequence of transformations that progressively transforms the target toward Gaussian. The resulting algorithm provides a computationally efficient way to construct flow-like transport maps: it requires only MFVI subproblems, avoids large-scale optimization, and yields transformations that are easy to invert and evaluate. In Bayesian inference tasks, we demonstrate that the proposed method achieves higher accuracy than standard MFVI, while maintaining much lower computational cost than conventional normalizing flows.

DeepScientist: Advancing Frontier-Pushing Scientific Findings Progressively

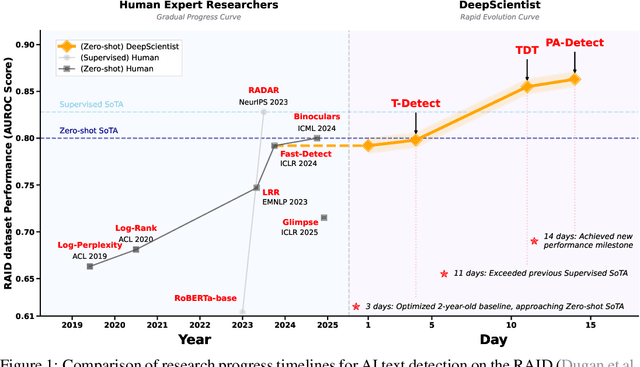
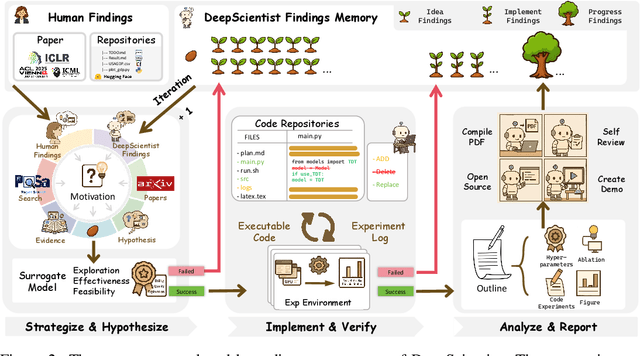
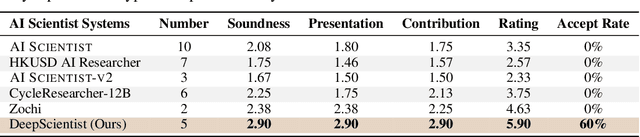
While previous AI Scientist systems can generate novel findings, they often lack the focus to produce scientifically valuable contributions that address pressing human-defined challenges. We introduce DeepScientist, a system designed to overcome this by conducting goal-oriented, fully autonomous scientific discovery over month-long timelines. It formalizes discovery as a Bayesian Optimization problem, operationalized through a hierarchical evaluation process consisting of "hypothesize, verify, and analyze". Leveraging a cumulative Findings Memory, this loop intelligently balances the exploration of novel hypotheses with exploitation, selectively promoting the most promising findings to higher-fidelity levels of validation. Consuming over 20,000 GPU hours, the system generated about 5,000 unique scientific ideas and experimentally validated approximately 1100 of them, ultimately surpassing human-designed state-of-the-art (SOTA) methods on three frontier AI tasks by 183.7\%, 1.9\%, and 7.9\%. This work provides the first large-scale evidence of an AI achieving discoveries that progressively surpass human SOTA on scientific tasks, producing valuable findings that genuinely push the frontier of scientific discovery. To facilitate further research into this process, we will open-source all experimental logs and system code at https://github.com/ResearAI/DeepScientist/.

Antithetic Noise in Diffusion Models

We initiate a systematic study of antithetic initial noise in diffusion models. Across unconditional models trained on diverse datasets, text-conditioned latent-diffusion models, and diffusion-posterior samplers, we find that pairing each initial noise with its negation consistently yields strongly negatively correlated samples. To explain this phenomenon, we combine experiments and theoretical analysis, leading to a symmetry conjecture that the learned score function is approximately affine antisymmetric (odd symmetry up to a constant shift), and provide evidence supporting it. Leveraging this negative correlation, we enable two applications: (1) enhancing image diversity in models like Stable Diffusion without quality loss, and (2) sharpening uncertainty quantification (e.g., up to 90% narrower confidence intervals) when estimating downstream statistics. Building on these gains, we extend the two-point pairing to a randomized quasi-Monte Carlo estimator, which further improves estimation accuracy. Our framework is training-free, model-agnostic, and adds no runtime overhead.

Towards Understanding Camera Motions in Any Video

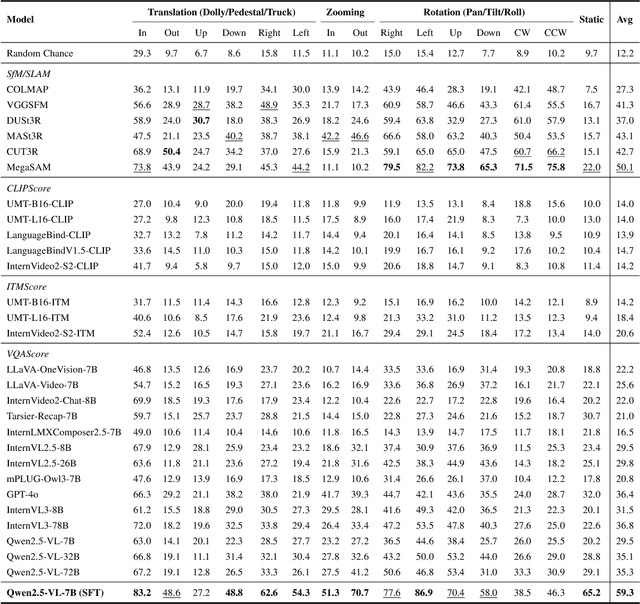
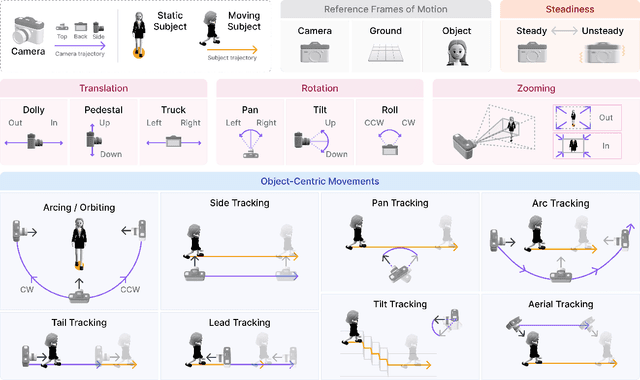
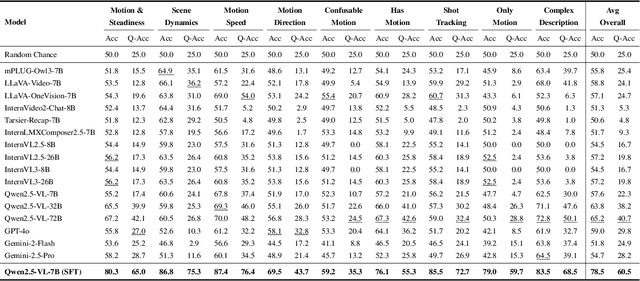
We introduce CameraBench, a large-scale dataset and benchmark designed to assess and improve camera motion understanding. CameraBench consists of ~3,000 diverse internet videos, annotated by experts through a rigorous multi-stage quality control process. One of our contributions is a taxonomy of camera motion primitives, designed in collaboration with cinematographers. We find, for example, that some motions like "follow" (or tracking) require understanding scene content like moving subjects. We conduct a large-scale human study to quantify human annotation performance, revealing that domain expertise and tutorial-based training can significantly enhance accuracy. For example, a novice may confuse zoom-in (a change of intrinsics) with translating forward (a change of extrinsics), but can be trained to differentiate the two. Using CameraBench, we evaluate Structure-from-Motion (SfM) and Video-Language Models (VLMs), finding that SfM models struggle to capture semantic primitives that depend on scene content, while VLMs struggle to capture geometric primitives that require precise estimation of trajectories. We then fine-tune a generative VLM on CameraBench to achieve the best of both worlds and showcase its applications, including motion-augmented captioning, video question answering, and video-text retrieval. We hope our taxonomy, benchmark, and tutorials will drive future efforts towards the ultimate goal of understanding camera motions in any video.

MultiConIR: Towards multi-condition Information Retrieval

In this paper, we introduce MultiConIR, the first benchmark designed to evaluate retrieval models in multi-condition scenarios. Unlike existing datasets that primarily focus on single-condition queries from search engines, MultiConIR captures real-world complexity by incorporating five diverse domains: books, movies, people, medical cases, and legal documents. We propose three tasks to systematically assess retrieval and reranking models on multi-condition robustness, monotonic relevance ranking, and query format sensitivity. Our findings reveal that existing retrieval and reranking models struggle with multi-condition retrieval, with rerankers suffering severe performance degradation as query complexity increases. We further investigate the performance gap between retrieval and reranking models, exploring potential reasons for these discrepancies, and analysis the impact of different pooling strategies on condition placement sensitivity. Finally, we highlight the strengths of GritLM and Nv-Embed, which demonstrate enhanced adaptability to multi-condition queries, offering insights for future retrieval models. The code and datasets are available at https://github.com/EIT-NLP/MultiConIR.

Transport Quasi-Monte Carlo

Quasi-Monte Carlo (QMC) is a powerful method for evaluating high-dimensional integrals. However, its use is typically limited to distributions where direct sampling is straightforward, such as the uniform distribution on the unit hypercube or the Gaussian distribution. For general target distributions with potentially unnormalized densities, leveraging the low-discrepancy property of QMC to improve accuracy remains challenging. We propose training a transport map to push forward the uniform distribution on the unit hypercube to approximate the target distribution. Inspired by normalizing flows, the transport map is constructed as a composition of simple, invertible transformations. To ensure that RQMC achieves its superior error rate, the transport map must satisfy specific regularity conditions. We introduce a flexible parametrization for the transport map that not only meets these conditions but is also expressive enough to model complex distributions. Our theoretical analysis establishes that the proposed transport QMC estimator achieves faster convergence rates than standard Monte Carlo, under mild and easily verifiable growth conditions on the integrand. Numerical experiments confirm the theoretical results, demonstrating the effectiveness of the proposed method in Bayesian inference tasks.

Langevin Quasi-Monte Carlo

Langevin Monte Carlo (LMC) and its stochastic gradient versions are powerful algorithms for sampling from complex high-dimensional distributions. To sample from a distribution with density $\pi(\theta)\propto \exp(-U(\theta)) $, LMC iteratively generates the next sample by taking a step in the gradient direction $\nabla U$ with added Gaussian perturbations. Expectations w.r.t. the target distribution $\pi$ are estimated by averaging over LMC samples. In ordinary Monte Carlo, it is well known that the estimation error can be substantially reduced by replacing independent random samples by quasi-random samples like low-discrepancy sequences. In this work, we show that the estimation error of LMC can also be reduced by using quasi-random samples. Specifically, we propose to use completely uniformly distributed (CUD) sequences with certain low-discrepancy property to generate the Gaussian perturbations. Under smoothness and convexity conditions, we prove that LMC with a low-discrepancy CUD sequence achieves smaller error than standard LMC. The theoretical analysis is supported by compelling numerical experiments, which demonstrate the effectiveness of our approach.

Joint BS Mode Selection and Beamforming Design for Cooperative Cell-Free ISAC Networks

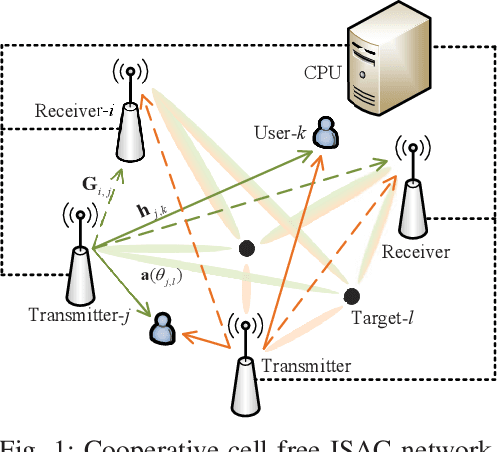
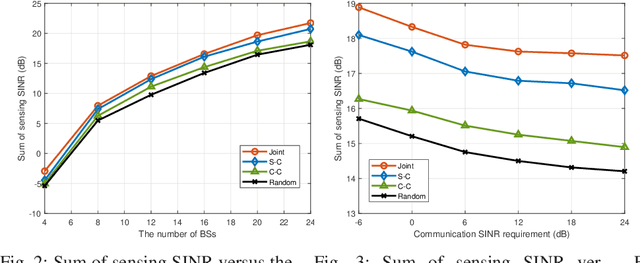
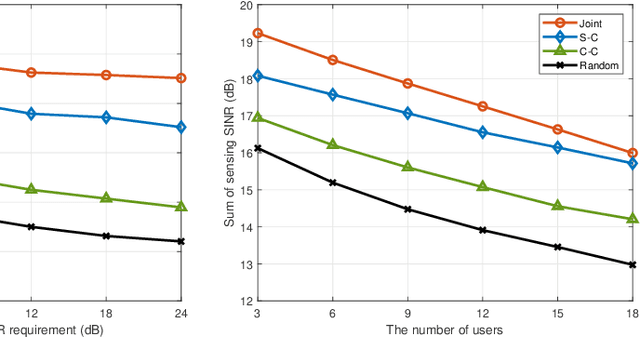
Owing to the promising ability of saving hardware cost and spectrum resources, integrated sensing and communication (ISAC) is regarded as a revolutionary technology for future sixth-generation (6G) networks. The mono-static ISAC systems considered in most of existing works can only obtain limited sensing performance due to the single observation angle and easily blocked transmission links, which motivates researchers to investigate cooperative ISAC networks. In order to further improve the degrees of freedom (DoFs) of cooperative ISAC networks, the transmitter-receiver selection, i.e., BS mode selection problem, is meaningful to be studied. However, to our best knowledge, this crucial problem has not been extensively studied in existing works. In this paper, we consider the joint BS mode selection, transmit beamforming, and receive filter design for cooperative cell-free ISAC networks, where multi-base stations (BSs) cooperatively serve communication users and detect targets. We aim to maximize the sum of sensing signal-to-interference-plus-noise ratio (SINR) under the communication SINR requirements, total power budget, and constraints on the numbers of transmitters and receivers. An efficient joint beamforming design algorithm and three different heuristic BS mode selection methods are proposed to solve this non-convex NP-hard problem. Simulation results demonstrates the advantages of cooperative ISAC networks, the importance of BS mode selection, and the effectiveness of our proposed joint design algorithms.

Joint BS-RIS-User Association and Beamforming Design for RIS-assisted Cellular Networks

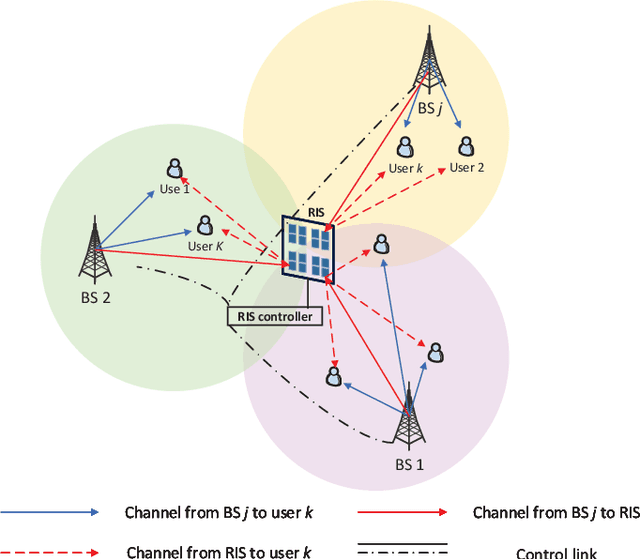
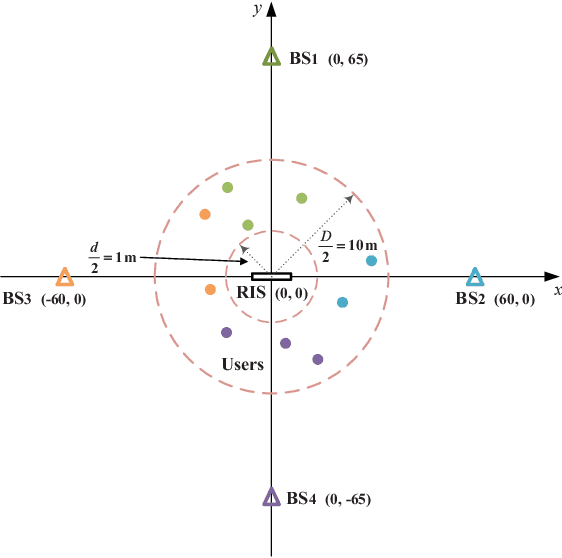
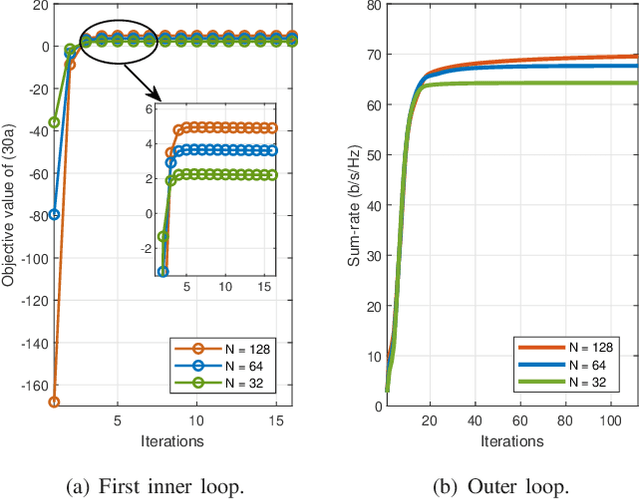
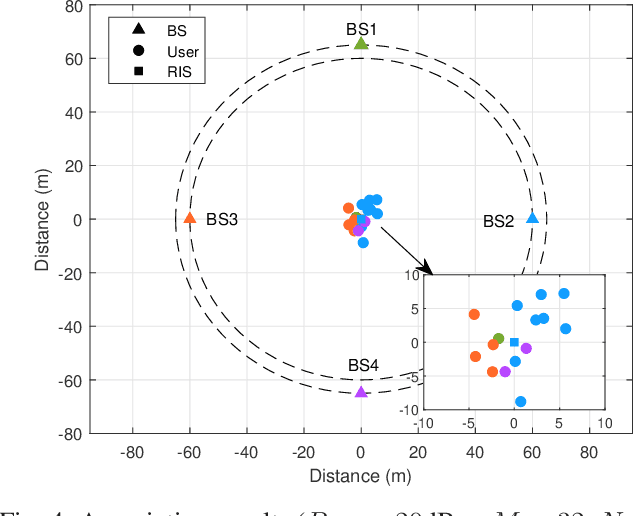
Reconfigurable intelligent surface (RIS) is a revolutionary technology for sixth-generation (6G) networks owing to its ability to manipulate wireless environments. As a frequency-selective device, RIS can only effectively shape the propagation of signals within a certain frequency band. Due to this frequency-selective property, the deployment of RIS in cellular networks will introduce a complicated base station (BS)-RIS-user association issue since adjacent BSs operate at different frequency bands. In this paper, with the consideration of the frequency-selective characteristics of RIS, we aim to jointly optimize BS-RIS-user association, active beamforming at BSs, and passive beamforming of RIS to maximize the sum-rate of a RIS-assisted cellular network. We first leverage $l_0$-norm to efficiently integrate BS-RIS-user association with active and passive beamforming. Then, we adopt fractional programming (FP) and block coordinate descent (BCD) methods to deal with logarithmic and fractional parts and decouple the joint association and beamforming design problem into several sub-problems. Efficient algorithms which combine $l_0$-norm approximation, majorization-minimization (MM), and alternating direction method of multipliers (ADMM) are developed to alternately solve the sub-problems. Extensive simulation results illustrate the importance of BS-RIS-user association optimization in RIS-assisted cellular networks and verify the effectiveness of the proposed joint association and beamforming design algorithm.

Black-box Selective Inference via Bootstrapping

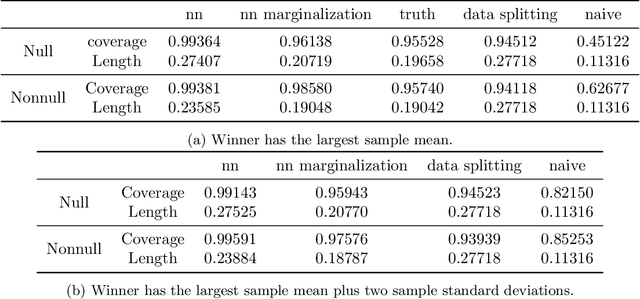
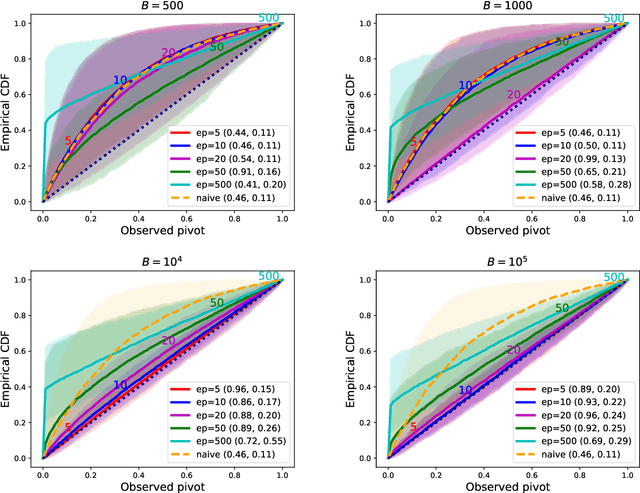
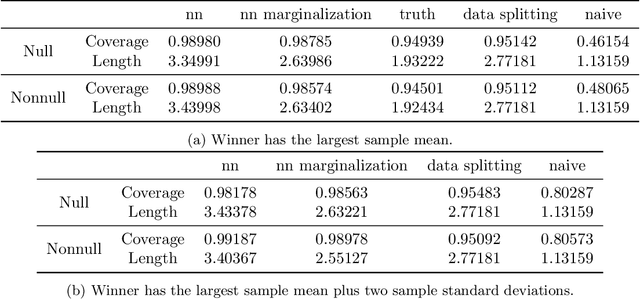
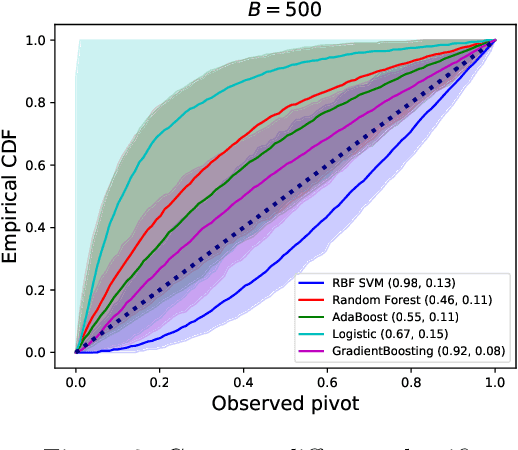
We propose a method for selective inference after a model selection procedure that is potentially a black box. In the conditional post-selection inference framework, a crucial quantity in determining the post-selection distribution of a test statistic is the probability of selecting the model conditional on the statistic. By repeatedly running the model selection procedure on bootstrapped datasets, we can generate training data with binary responses indicating the selection event as well as specially designed covariates, which are then used to learn the selection probability. We prove that the constructed confidence intervals are asymptotically valid if we can learn the selection probability sufficiently well around a neighborhood of the target parameter. The validity of the proposed algorithm is verified by several examples.