Black-box Selective Inference via Bootstrapping
Paper and Code
Mar 28, 2022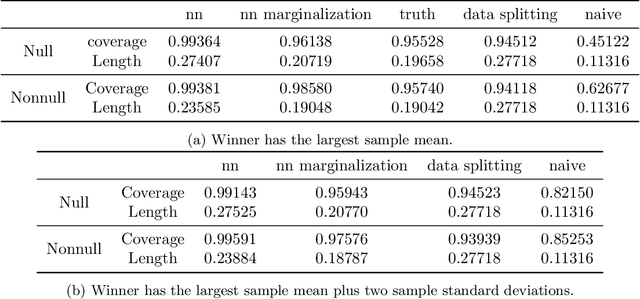
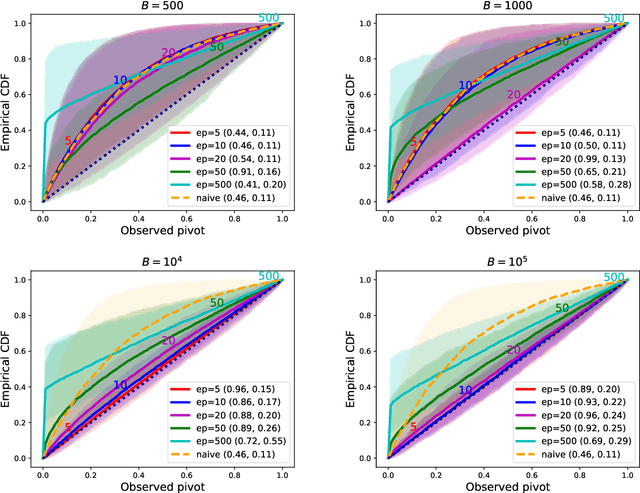
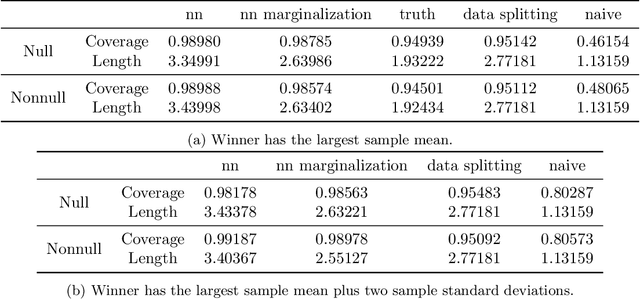
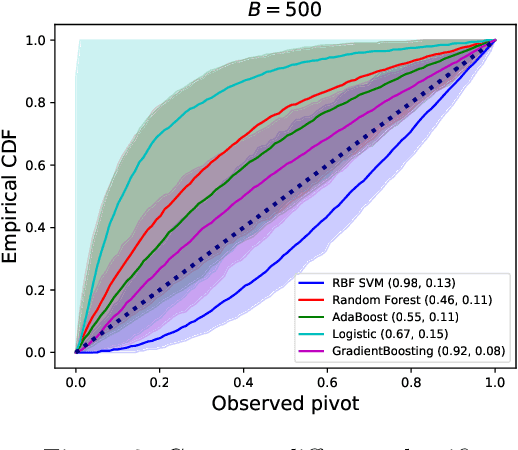
We propose a method for selective inference after a model selection procedure that is potentially a black box. In the conditional post-selection inference framework, a crucial quantity in determining the post-selection distribution of a test statistic is the probability of selecting the model conditional on the statistic. By repeatedly running the model selection procedure on bootstrapped datasets, we can generate training data with binary responses indicating the selection event as well as specially designed covariates, which are then used to learn the selection probability. We prove that the constructed confidence intervals are asymptotically valid if we can learn the selection probability sufficiently well around a neighborhood of the target parameter. The validity of the proposed algorithm is verified by several examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge