Yuting Ng
Duke University
Elliptic Loss Regularization
Mar 04, 2025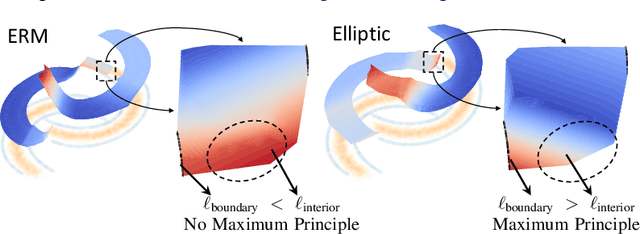

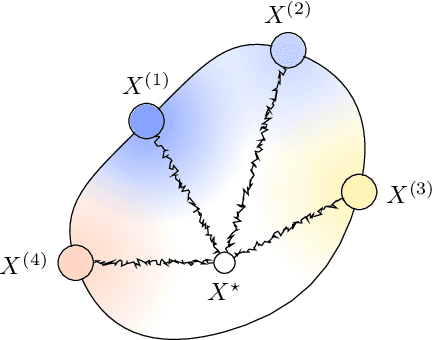
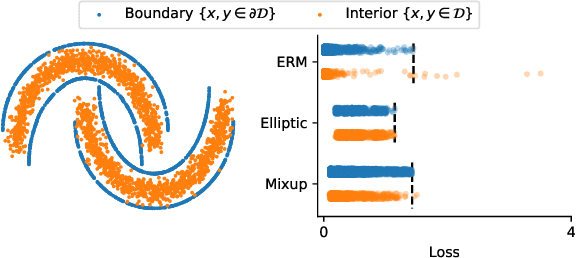
Abstract:Regularizing neural networks is important for anticipating model behavior in regions of the data space that are not well represented. In this work, we propose a regularization technique for enforcing a level of smoothness in the mapping between the data input space and the loss value. We specify the level of regularity by requiring that the loss of the network satisfies an elliptic operator over the data domain. To do this, we modify the usual empirical risk minimization objective such that we instead minimize a new objective that satisfies an elliptic operator over points within the domain. This allows us to use existing theory on elliptic operators to anticipate the behavior of the error for points outside the training set. We propose a tractable computational method that approximates the behavior of the elliptic operator while being computationally efficient. Finally, we analyze the properties of the proposed regularization to understand the performance on common problems of distribution shift and group imbalance. Numerical experiments confirm the utility of the proposed regularization technique.
Distributionally Robust Optimization as a Scalable Framework to Characterize Extreme Value Distributions
Jul 31, 2024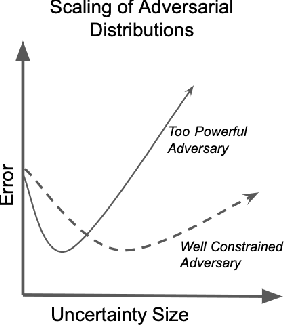


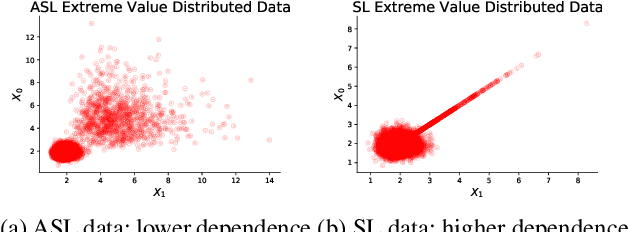
Abstract:The goal of this paper is to develop distributionally robust optimization (DRO) estimators, specifically for multidimensional Extreme Value Theory (EVT) statistics. EVT supports using semi-parametric models called max-stable distributions built from spatial Poisson point processes. While powerful, these models are only asymptotically valid for large samples. However, since extreme data is by definition scarce, the potential for model misspecification error is inherent to these applications, thus DRO estimators are natural. In order to mitigate over-conservative estimates while enhancing out-of-sample performance, we study DRO estimators informed by semi-parametric max-stable constraints in the space of point processes. We study both tractable convex formulations for some problems of interest (e.g. CVaR) and more general neural network based estimators. Both approaches are validated using synthetically generated data, recovering prescribed characteristics, and verifying the efficacy of the proposed techniques. Additionally, the proposed method is applied to a real data set of financial returns for comparison to a previous analysis. We established the proposed model as a novel formulation in the multivariate EVT domain, and innovative with respect to performance when compared to relevant alternate proposals.
Neural McKean-Vlasov Processes: Distributional Dependence in Diffusion Processes
Apr 15, 2024Abstract:McKean-Vlasov stochastic differential equations (MV-SDEs) provide a mathematical description of the behavior of an infinite number of interacting particles by imposing a dependence on the particle density. As such, we study the influence of explicitly including distributional information in the parameterization of the SDE. We propose a series of semi-parametric methods for representing MV-SDEs, and corresponding estimators for inferring parameters from data based on the properties of the MV-SDE. We analyze the characteristics of the different architectures and estimators, and consider their applicability in relevant machine learning problems. We empirically compare the performance of the different architectures and estimators on real and synthetic datasets for time series and probabilistic modeling. The results suggest that explicitly including distributional dependence in the parameterization of the SDE is effective in modeling temporal data with interaction under an exchangeability assumption while maintaining strong performance for standard It\^o-SDEs due to the richer class of probability flows associated with MV-SDEs.
PrACTiS: Perceiver-Attentional Copulas for Time Series
Oct 03, 2023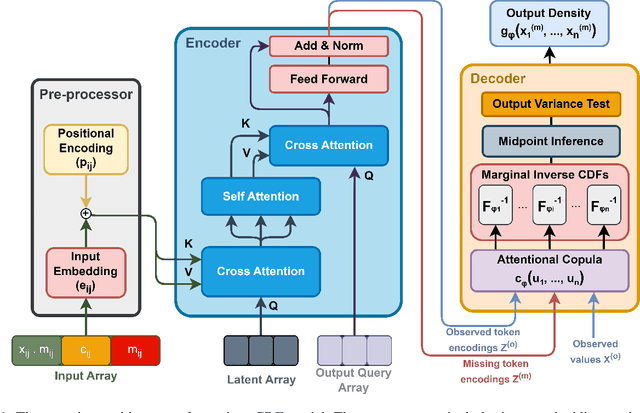
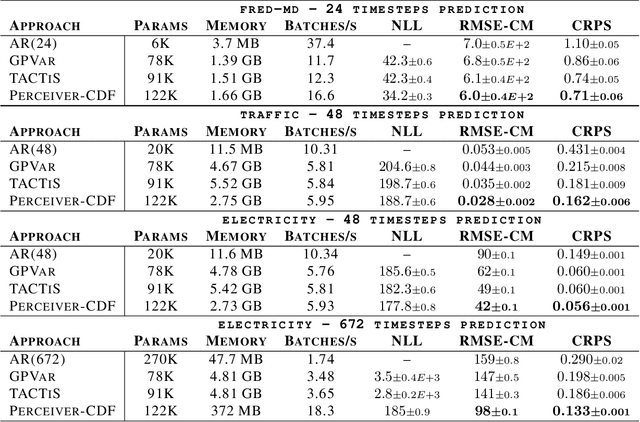
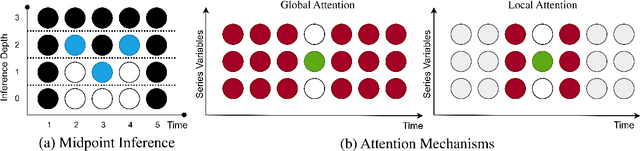
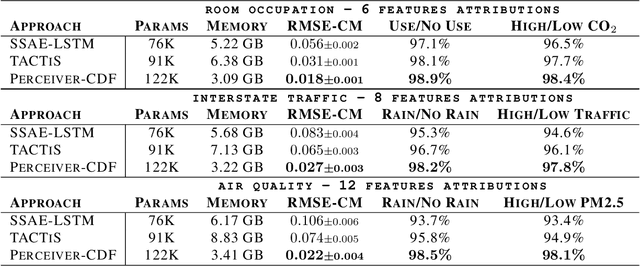
Abstract:Transformers incorporating copula structures have demonstrated remarkable performance in time series prediction. However, their heavy reliance on self-attention mechanisms demands substantial computational resources, thus limiting their practical utility across a wide range of tasks. In this work, we present a model that combines the perceiver architecture with a copula structure to enhance time-series forecasting. By leveraging the perceiver as the encoder, we efficiently transform complex, high-dimensional, multimodal data into a compact latent space, thereby significantly reducing computational demands. To further reduce complexity, we introduce midpoint inference and local attention mechanisms, enabling the model to capture dependencies within imputed samples effectively. Subsequently, we deploy the copula-based attention and output variance testing mechanism to capture the joint distribution of missing data, while simultaneously mitigating error propagation during prediction. Our experimental results on the unimodal and multimodal benchmarks showcase a consistent 20\% improvement over the state-of-the-art methods, while utilizing less than half of available memory resources.
Individual Treatment Effects in Extreme Regimes
Jun 20, 2023Abstract:Understanding individual treatment effects in extreme regimes is important for characterizing risks associated with different interventions. This is hindered by the fact that extreme regime data may be hard to collect, as it is scarcely observed in practice. In addressing this issue, we propose a new framework for estimating the individual treatment effect in extreme regimes (ITE$_2$). Specifically, we quantify this effect by the changes in the tail decay rates of potential outcomes in the presence or absence of the treatment. Subsequently, we establish conditions under which ITE$_2$ may be calculated and develop algorithms for its computation. We demonstrate the efficacy of our proposed method on various synthetic and semi-synthetic datasets.
Inference and Sampling of Point Processes from Diffusion Excursions
Jun 01, 2023Abstract:Point processes often have a natural interpretation with respect to a continuous process. We propose a point process construction that describes arrival time observations in terms of the state of a latent diffusion process. In this framework, we relate the return times of a diffusion in a continuous path space to new arrivals of the point process. This leads to a continuous sample path that is used to describe the underlying mechanism generating the arrival distribution. These models arise in many disciplines, such as financial settings where actions in a market are determined by a hidden continuous price or in neuroscience where a latent stimulus generates spike trains. Based on the developments in It\^o's excursion theory, we propose methods for inferring and sampling from the point process derived from the latent diffusion process. We illustrate the approach with numerical examples using both simulated and real data. The proposed methods and framework provide a basis for interpreting point processes through the lens of diffusions.
Inference and Sampling for Archimax Copulas
May 27, 2022

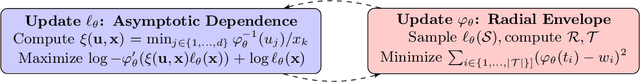

Abstract:Understanding multivariate dependencies in both the bulk and the tails of a distribution is an important problem for many applications, such as ensuring algorithms are robust to observations that are infrequent but have devastating effects. Archimax copulas are a family of distributions endowed with a precise representation that allows simultaneous modeling of the bulk and the tails of a distribution. Rather than separating the two as is typically done in practice, incorporating additional information from the bulk may improve inference of the tails, where observations are limited. Building on the stochastic representation of Archimax copulas, we develop a non-parametric inference method and sampling algorithm. Our proposed methods, to the best of our knowledge, are the first that allow for highly flexible and scalable inference and sampling algorithms, enabling the increased use of Archimax copulas in practical settings. We experimentally compare to state-of-the-art density modeling techniques, and the results suggest that the proposed method effectively extrapolates to the tails while scaling to higher dimensional data. Our findings suggest that the proposed algorithms can be used in a variety of applications where understanding the interplay between the bulk and the tails of a distribution is necessary, such as healthcare and safety.
Generative Archimedean Copulas
Feb 24, 2021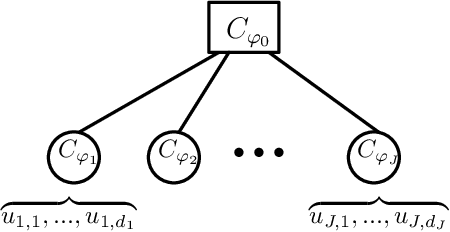
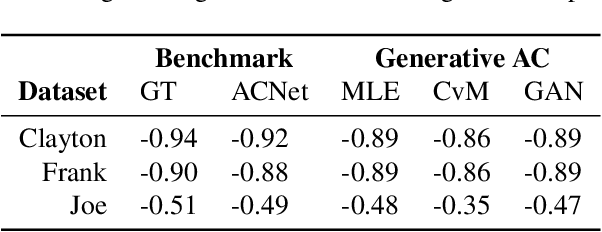
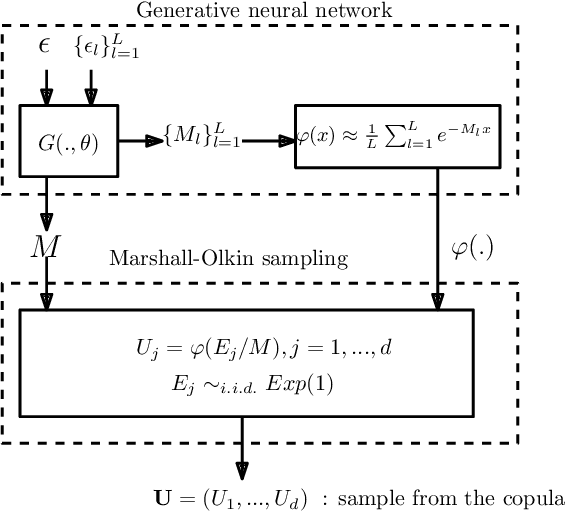
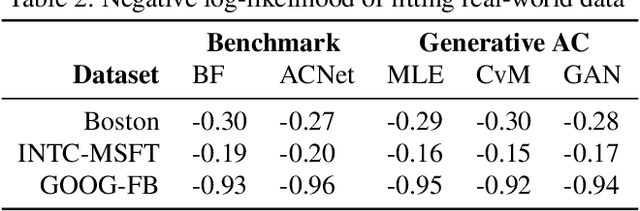
Abstract:We propose a new generative modeling technique for learning multidimensional cumulative distribution functions (CDFs) in the form of copulas. Specifically, we consider certain classes of copulas known as Archimedean and hierarchical Archimedean copulas, popular for their parsimonious representation and ability to model different tail dependencies. We consider their representation as mixture models with Laplace transforms of latent random variables from generative neural networks. This alternative representation allows for easy sampling and computational efficiencies especially in high dimensions. We additionally describe multiple methods for optimizing the model parameters. Finally, we present empirical results that demonstrate the efficacy of our proposed method in learning multidimensional CDFs and its computational efficiency compared to existing methods.
Robust Marine Buoy Placement for Ship Detection Using Dropout K-Means
Feb 20, 2020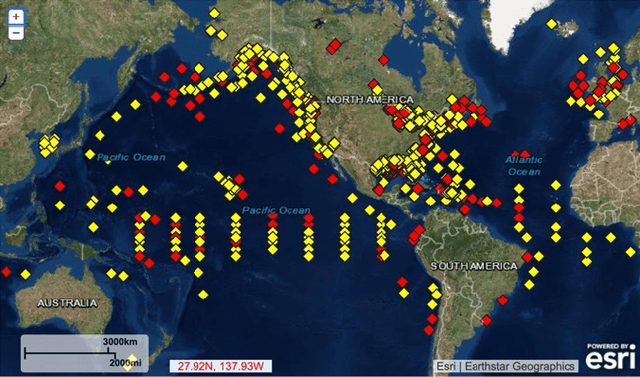

Abstract:Marine buoys aid in the battle against Illegal, Unreported and Unregulated (IUU) fishing by detecting fishing vessels in their vicinity. Marine buoys, however, may be disrupted by natural causes and buoy vandalism. In this paper, we formulate marine buoy placement as a clustering problem, and propose dropout k-means and dropout k-median to improve placement robustness to buoy disruption. We simulated the passage of ships in the Gabonese waters near West Africa using historical Automatic Identification System (AIS) data, then compared the ship detection probability of dropout k-means to classic k-means and dropout k-median to classic k-median. With 5 buoys, the buoy arrangement computed by classic k-means, dropout k-means, classic k-median and dropout k-median have ship detection probabilities of 38%, 45%, 48% and 52%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge