Characteristic Neural Ordinary Differential Equations

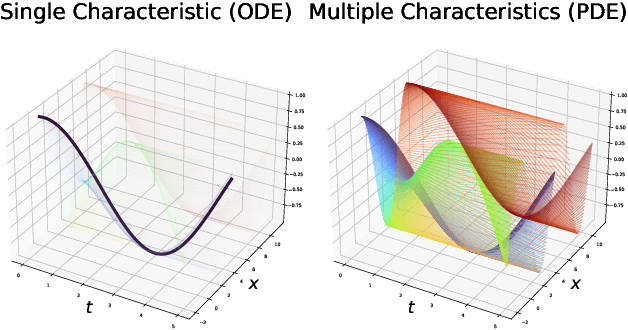
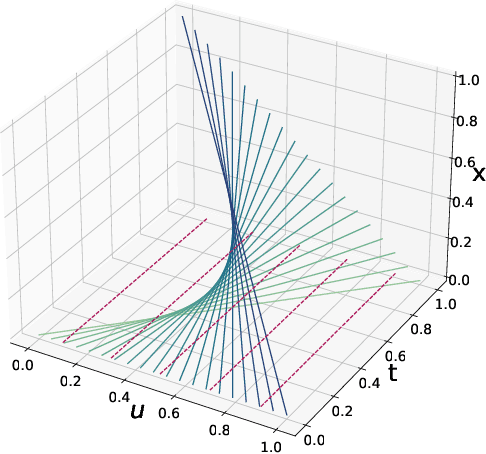
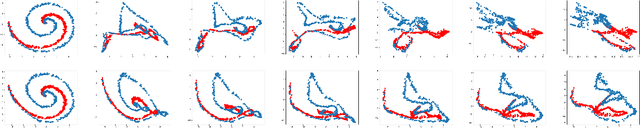
We propose Characteristic Neural Ordinary Differential Equations (C-NODEs), a framework for extending Neural Ordinary Differential Equations (NODEs) beyond ODEs. While NODEs model the evolution of the latent state as the solution to an ODE, the proposed C-NODE models the evolution of the latent state as the solution of a family of first-order quasi-linear partial differential equations (PDE) on their characteristics, defined as curves along which the PDEs reduce to ODEs. The reduction, in turn, allows the application of the standard frameworks for solving ODEs to PDE settings. Additionally, the proposed framework can be cast as an extension of existing NODE architectures, thereby allowing the use of existing black-box ODE solvers. We prove that the C-NODE framework extends the classical NODE by exhibiting functions that cannot be represented by NODEs but are representable by C-NODEs. We further investigate the efficacy of the C-NODE framework by demonstrating its performance in many synthetic and real data scenarios. Empirical results demonstrate the improvements provided by the proposed method for CIFAR-10, SVHN, and MNIST datasets under a similar computational budget as the existing NODE methods.

Generative Archimedean Copulas

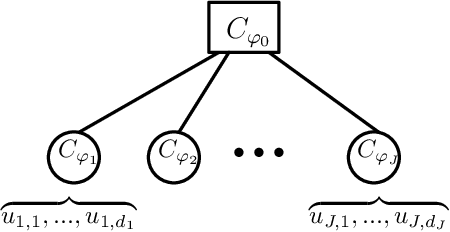
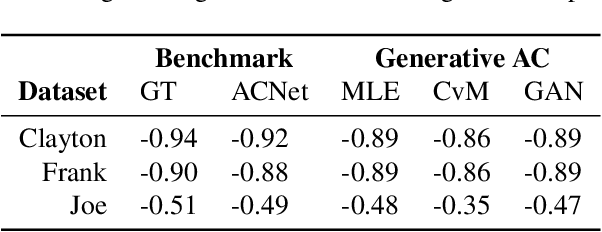
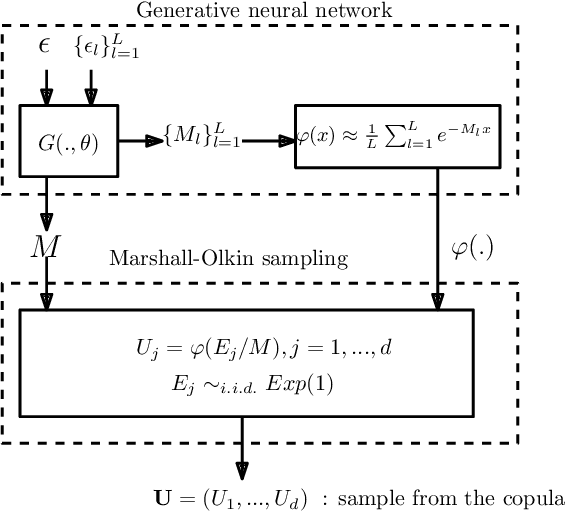
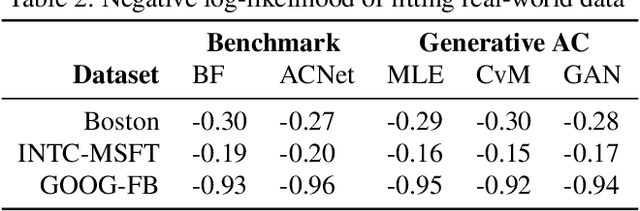
We propose a new generative modeling technique for learning multidimensional cumulative distribution functions (CDFs) in the form of copulas. Specifically, we consider certain classes of copulas known as Archimedean and hierarchical Archimedean copulas, popular for their parsimonious representation and ability to model different tail dependencies. We consider their representation as mixture models with Laplace transforms of latent random variables from generative neural networks. This alternative representation allows for easy sampling and computational efficiencies especially in high dimensions. We additionally describe multiple methods for optimizing the model parameters. Finally, we present empirical results that demonstrate the efficacy of our proposed method in learning multidimensional CDFs and its computational efficiency compared to existing methods.

Deep Extreme Value Copulas for Estimation and Sampling

We propose a new method for modeling the distribution function of high dimensional extreme value distributions. The Pickands dependence function models the relationship between the covariates in the tails, and we learn this function using a neural network that is designed to satisfy its required properties. Moreover, we present new methods for recovering the spectral representation of extreme distributions and propose a generative model for sampling from extreme copulas. Numerical examples are provided demonstrating the efficacy and promise of our proposed methods.

Fisher Auto-Encoders

It has been conjectured that the Fisher divergence is more robust to model uncertainty than the conventional Kullback-Leibler (KL) divergence. This motivates the design of a new class of robust generative auto-encoders (AE) referred to as Fisher auto-encoders. Our approach is to design Fisher AEs by minimizing the Fisher divergence between the intractable joint distribution of observed data and latent variables, with that of the postulated/modeled joint distribution. In contrast to KL-based variational AEs (VAEs), the Fisher AE can exactly quantify the distance between the true and the model-based posterior distributions. Qualitative and quantitative results are provided on both MNIST and celebA datasets demonstrating the competitive performance of Fisher AEs in terms of robustness compared to other AEs such as VAEs and Wasserstein AEs.

Improved Design of Quadratic Discriminant Analysis Classifier in Unbalanced Settings

The use of quadratic discriminant analysis (QDA) or its regularized version (R-QDA) for classification is often not recommended, due to its well-acknowledged high sensitivity to the estimation noise of the covariance matrix. This becomes all the more the case in unbalanced data settings for which it has been found that R-QDA becomes equivalent to the classifier that assigns all observations to the same class. In this paper, we propose an improved R-QDA that is based on the use of two regularization parameters and a modified bias, properly chosen to avoid inappropriate behaviors of R-QDA in unbalanced settings and to ensure the best possible classification performance. The design of the proposed classifier builds on a refined asymptotic analysis of its performance when the number of samples and that of features grow large simultaneously, which allows to cope efficiently with the high-dimensionality frequently met within the big data paradigm. The performance of the proposed classifier is assessed on both real and synthetic data sets and was shown to be much better than what one would expect from a traditional R-QDA.

Risk Convergence of Centered Kernel Ridge Regression with Large Dimensional Data

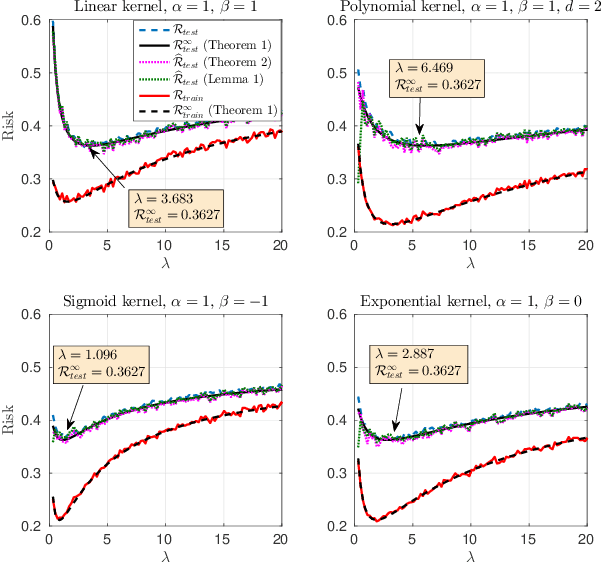
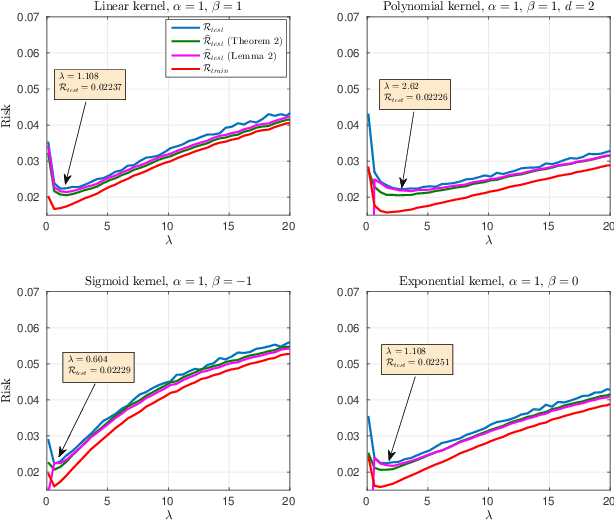
This paper carries out a large dimensional analysis of a variation of kernel ridge regression that we call \emph{centered kernel ridge regression} (CKRR), also known in the literature as kernel ridge regression with offset. This modified technique is obtained by accounting for the bias in the regression problem resulting in the old kernel ridge regression but with \emph{centered} kernels. The analysis is carried out under the assumption that the data is drawn from a Gaussian distribution and heavily relies on tools from random matrix theory (RMT). Under the regime in which the data dimension and the training size grow infinitely large with fixed ratio and under some mild assumptions controlling the data statistics, we show that both the empirical and the prediction risks converge to a deterministic quantities that describe in closed form fashion the performance of CKRR in terms of the data statistics and dimensions. Inspired by this theoretical result, we subsequently build a consistent estimator of the prediction risk based on the training data which allows to optimally tune the design parameters. A key insight of the proposed analysis is the fact that asymptotically a large class of kernels achieve the same minimum prediction risk. This insight is validated with both synthetic and real data.

A Large Dimensional Study of Regularized Discriminant Analysis Classifiers

This article carries out a large dimensional analysis of standard regularized discriminant analysis classifiers designed on the assumption that data arise from a Gaussian mixture model with different means and covariances. The analysis relies on fundamental results from random matrix theory (RMT) when both the number of features and the cardinality of the training data within each class grow large at the same pace. Under mild assumptions, we show that the asymptotic classification error approaches a deterministic quantity that depends only on the means and covariances associated with each class as well as the problem dimensions. Such a result permits a better understanding of the performance of regularized discriminant analsysis, in practical large but finite dimensions, and can be used to determine and pre-estimate the optimal regularization parameter that minimizes the misclassification error probability. Despite being theoretically valid only for Gaussian data, our findings are shown to yield a high accuracy in predicting the performances achieved with real data sets drawn from the popular USPS data base, thereby making an interesting connection between theory and practice.