Performance Analysis of Joint Antenna Selection and Precoding Methods in Multi-user Massive MISO

This paper presents a performance analysis of two distinct techniques for antenna selection and precoding in downlink multi-user massive multiple-input single-output systems with limited dynamic range power amplifiers. Both techniques are derived from the original formulation of the regularized-zero forcing precoder, designed as the solution to minimizing a regularized distortion. Based on this, the first technique, called the $\ell_1$-norm precoder, adopts an $\ell_1$-norm regularization term to encourage sparse solutions, thereby enabling antenna selection. The second technique, termed the thresholded $\ell_1$-norm precoder, involves post-processing the precoder solution obtained from the first method by applying an entry-wise thresholding operation. This work conducts a precise performance analysis to compare these two techniques. The analysis leverages the Gaussian min-max theorem which is effective for examining the asymptotic behavior of optimization problems without explicit solutions. While the analysis of the $\ell_1$-norm precoder follows the conventional Gaussian min-max theorem framework, understanding the thresholded $\ell_1$-norm precoder is more complex due to the non-linear behavior introduced by the thresholding operation. To address this complexity, we develop a novel Gaussian min-max theorem tailored to these scenarios. We provide precise asymptotic behavior analysis of the precoders, focusing on metrics such as received signal-to-noise and distortion ratio and bit error rate. Our analysis demonstrates that the thresholded $\ell_1$-norm precoder can offer superior performance when the threshold parameter is carefully selected. Simulations confirm that the asymptotic results are accurate for systems equipped with hundreds of antennas at the base station, serving dozens of user terminals.

Precoding for High Throughput Satellite Communication Systems: A Survey

With the expanding demand for high data rates and extensive coverage, high throughput satellite (HTS) communication systems are emerging as a key technology for future communication generations. However, current frequency bands are increasingly congested. Until the maturity of communication systems to operate on higher bands, the solution is to exploit the already existing frequency bands more efficiently. In this context, precoding emerges as one of the prolific approaches to increasing spectral efficiency. This survey presents an overview and a classification of the recent precoding techniques for HTS communication systems from two main perspectives: 1) a problem formulation perspective and 2) a system design perspective. From a problem formulation point of view, precoding techniques are classified according to the precoding objective, group, and level. From a system design standpoint, precoding is categorized based on the system architecture, the precoding implementation, and the type of the provided service. Further, practical system impairments are discussed, and robust precoding techniques are presented. Finally, future trends in precoding for satellites are addressed to spur further research.

Max-Min Data Rate Optimization for RIS-aided Uplink Communications with Green Constraints

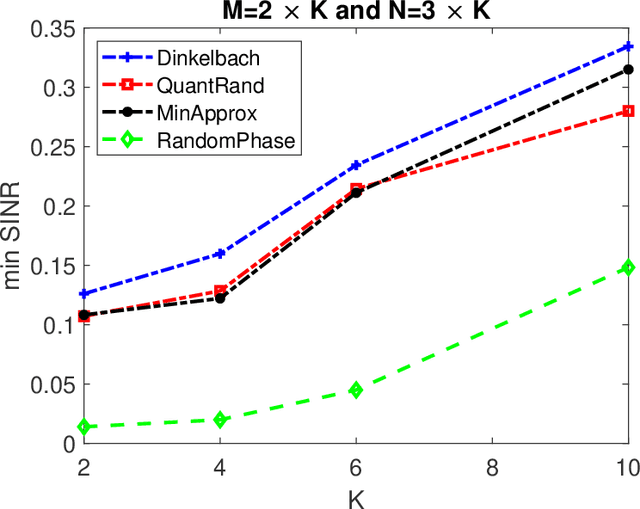
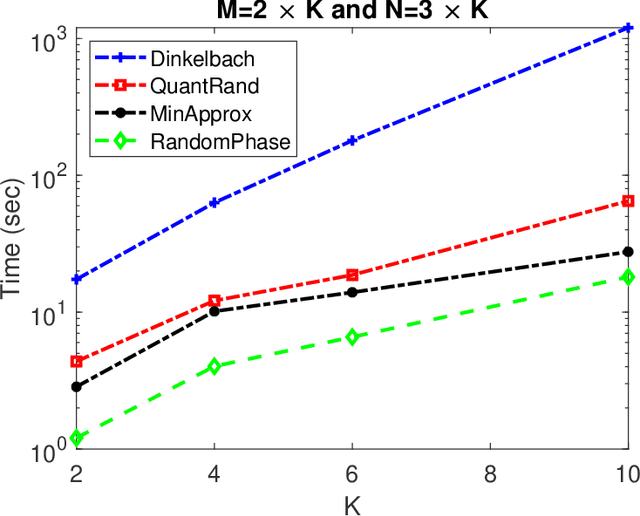
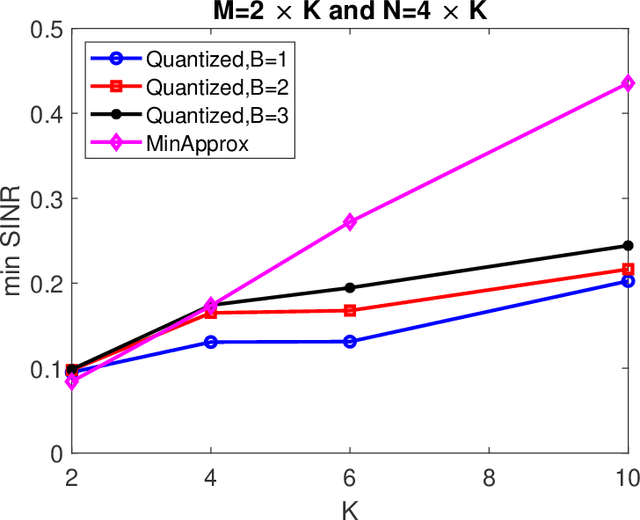
Smart radio environments aided by reconfigurable intelligent reflecting surfaces (RIS) have attracted much research attention recently. We propose a joint optimization strategy for beamforming, RIS phases, and power allocation to maximize the minimum SINR of an uplink RIS-aided communication system. The users are subject to constraints on their transmit power. We derive a closed-form expression for the beam forming vectors and a geometric programming-based solution for power allocation. We also propose two solutions for optimizing the phase shifts at the RIS, one based on the matrix lifting method and one using an approximation for the minimum function. We also propose a heuristic algorithm for optimizing quantized phase shift values. The proposed algorithms are of practical interest for systems with constraints on the maximum allowable electromagnetic field exposure. For instance, considering $24$-element RIS, $12$-antenna BS, and $6$ users, numerical results show that the proposed algorithm achieves close to $300 \%$ gain in terms of minimum SINR compared to a scheme with random RIS phases.

Sharp Analysis of RLS-based Digital Precoder with Limited PAPR in Massive MIMO

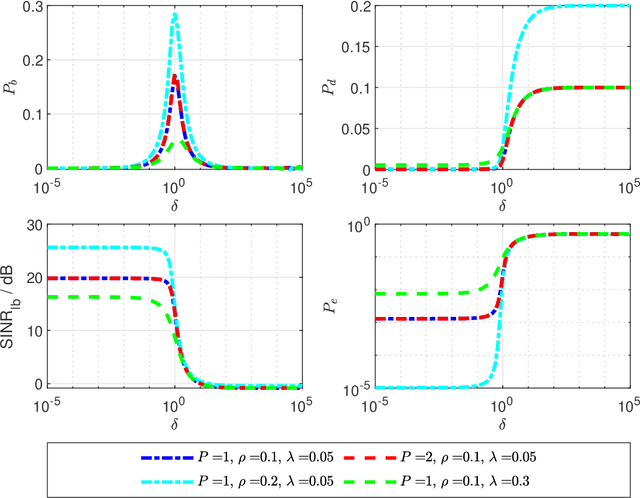
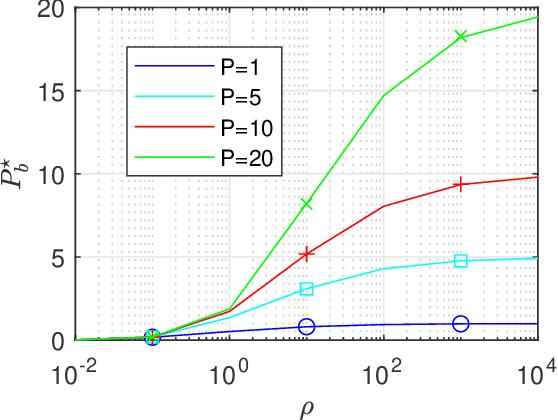
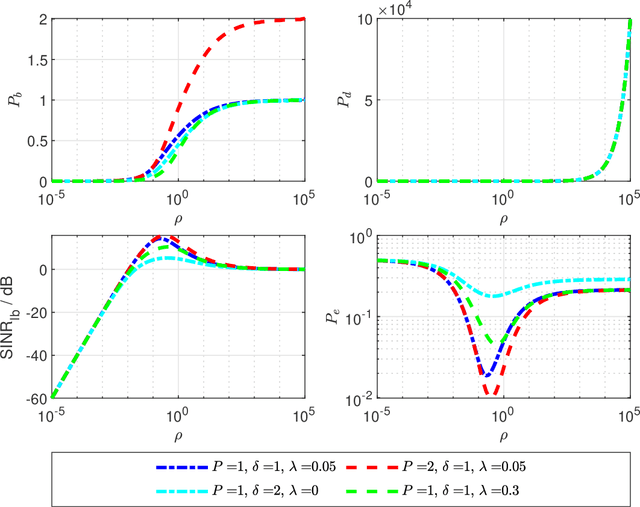
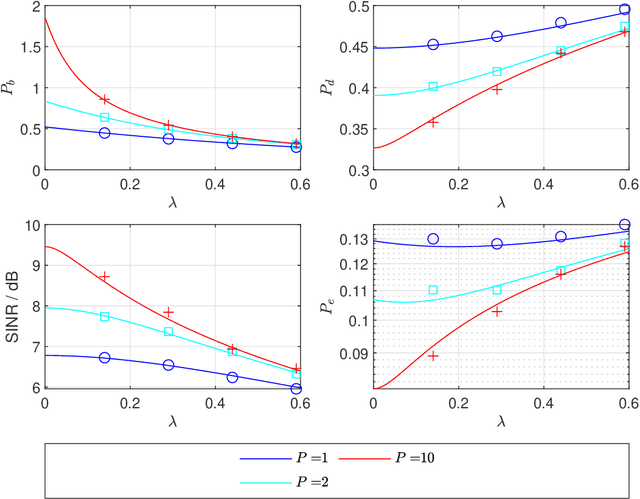
This paper focuses on the performance analysis of a class of limited peak-to-average power ratio (PAPR) precoders for downlink multi-user massive multiple-input multiple-output (MIMO) systems. Contrary to conventional precoding approaches based on simple linear precoders maximum ratio transmission (MRT) and regularized zero forcing (RZF), the precoders in this paper are obtained by solving a convex optimization problem. To be specific, for the precoders we analyze in this paper, the power of each precoded symbol entry is restricted, which allows them to present a reduced PAPR at each antenna. By using the Convex Gaussian Min-max Theorem (CGMT), we analytically characterize the empirical distribution of the precoded vector and the joint empirical distribution between the distortion and the intended symbol vector. This allows us to study the performance of these precoders in terms of per-antenna power, per-user distortion power, signal to interference and noise ratio, and bit error probability. We show that for this class of precoders, there is an optimal transmit power that maximizes the system performance.

A New Analytical Approximation of the Fluid Antenna System Channel

Fluid antenna systems (FAS) are an emerging technology that promises a significant diversity gain even in the smallest spaces. Motivated by the groundbreaking potentials of liquid antennas, researchers in the wireless communication community are investigating a novel antenna system where a single antenna can freely switch positions along a small linear space to pick the strongest received signal. However, the FAS positions do not necessarily follow the ever-existing rule separating them by at least half the radiation wavelength. Previous work in the literature parameterized the channels of the FAS ports simply enough to provide a single-integral expression of the probability of outage and various insights on the achievable performance. Nevertheless, this channel model may not accurately capture the correlation between the ports, given by Jake's model. This work builds on the state-of-the-art and accurately approximates the FAS channel while maintaining analytical tractability. The approximation is performed in two stages. The first stage approximation considerably reduces the number of multi-fold integrals in the probability of outage expression, while the second stage approximation provides a single integral representation of the FAS probability of outage. Further, the performance of such innovative technology is investigated under a less-idealized correlation model. Numerical results validate our approximations of the FAS channel model and demonstrate a limited performance gain under realistic assumptions. Further, our work opens the door for future research to investigate scenarios in which the FAS provides a performance gain compared to the current multiple antennas solutions.

Weight Vector Tuning and Asymptotic Analysis of Binary Linear Classifiers

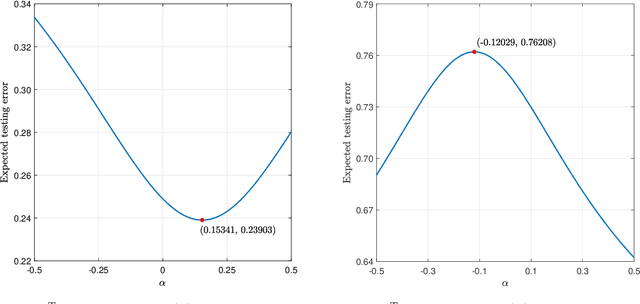
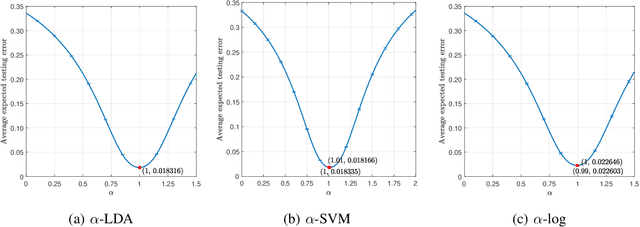
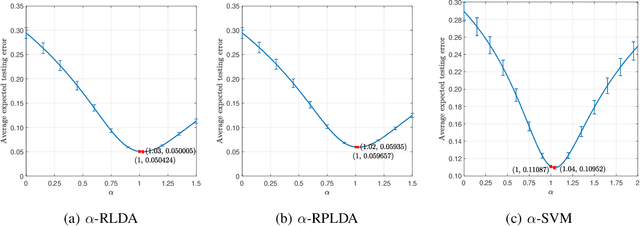
Unlike its intercept, a linear classifier's weight vector cannot be tuned by a simple grid search. Hence, this paper proposes weight vector tuning of a generic binary linear classifier through the parameterization of a decomposition of the discriminant by a scalar which controls the trade-off between conflicting informative and noisy terms. By varying this parameter, the original weight vector is modified in a meaningful way. Applying this method to a number of linear classifiers under a variety of data dimensionality and sample size settings reveals that the classification performance loss due to non-optimal native hyperparameters can be compensated for by weight vector tuning. This yields computational savings as the proposed tuning method reduces to tuning a scalar compared to tuning the native hyperparameter, which may involve repeated weight vector generation along with its burden of optimization, dimensionality reduction, etc., depending on the classifier. It is also found that weight vector tuning significantly improves the performance of Linear Discriminant Analysis (LDA) under high estimation noise. Proceeding from this second finding, an asymptotic study of the misclassification probability of the parameterized LDA classifier in the growth regime where the data dimensionality and sample size are comparable is conducted. Using random matrix theory, the misclassification probability is shown to converge to a quantity that is a function of the true statistics of the data. Additionally, an estimator of the misclassification probability is derived. Finally, computationally efficient tuning of the parameter using this estimator is demonstrated on real data.

High-Dimensional Quadratic Discriminant Analysis under Spiked Covariance Model

Quadratic discriminant analysis (QDA) is a widely used classification technique that generalizes the linear discriminant analysis (LDA) classifier to the case of distinct covariance matrices among classes. For the QDA classifier to yield high classification performance, an accurate estimation of the covariance matrices is required. Such a task becomes all the more challenging in high dimensional settings, wherein the number of observations is comparable with the feature dimension. A popular way to enhance the performance of QDA classifier under these circumstances is to regularize the covariance matrix, giving the name regularized QDA (R-QDA) to the corresponding classifier. In this work, we consider the case in which the population covariance matrix has a spiked covariance structure, a model that is often assumed in several applications. Building on the classical QDA, we propose a novel quadratic classification technique, the parameters of which are chosen such that the fisher-discriminant ratio is maximized. Numerical simulations show that the proposed classifier not only outperforms the classical R-QDA for both synthetic and real data but also requires lower computational complexity, making it suitable to high dimensional settings.

Improved Design of Quadratic Discriminant Analysis Classifier in Unbalanced Settings

The use of quadratic discriminant analysis (QDA) or its regularized version (R-QDA) for classification is often not recommended, due to its well-acknowledged high sensitivity to the estimation noise of the covariance matrix. This becomes all the more the case in unbalanced data settings for which it has been found that R-QDA becomes equivalent to the classifier that assigns all observations to the same class. In this paper, we propose an improved R-QDA that is based on the use of two regularization parameters and a modified bias, properly chosen to avoid inappropriate behaviors of R-QDA in unbalanced settings and to ensure the best possible classification performance. The design of the proposed classifier builds on a refined asymptotic analysis of its performance when the number of samples and that of features grow large simultaneously, which allows to cope efficiently with the high-dimensionality frequently met within the big data paradigm. The performance of the proposed classifier is assessed on both real and synthetic data sets and was shown to be much better than what one would expect from a traditional R-QDA.

Asymptotic Analysis of an Ensemble of Randomly Projected Linear Discriminants

Datasets from the fields of bioinformatics, chemometrics, and face recognition are typically characterized by small samples of high-dimensional data. Among the many variants of linear discriminant analysis that have been proposed in order to rectify the issues associated with classification in such a setting, the classifier in [1], composed of an ensemble of randomly projected linear discriminants, seems especially promising; it is computationally efficient and, with the optimal projection dimension parameter setting, is competitive with the state-of-the-art. In this work, we seek to further understand the behavior of this classifier through asymptotic analysis. Under the assumption of a growth regime in which the dataset and projection dimensions grow at constant rates to each other, we use random matrix theory to derive asymptotic misclassification probabilities showing the effect of the ensemble as a regularization of the data sample covariance matrix. The asymptotic errors further help to identify situations in which the ensemble offers a performance advantage. We also develop a consistent estimator of the misclassification probability as an alternative to the computationally-costly cross-validation estimator, which is conventionally used for parameter tuning. Finally, we demonstrate the use of our estimator for tuning the projection dimension on both real and synthetic data.

A Model of Double Descent for High-dimensional Binary Linear Classification

We consider a model for logistic regression where only a subset of features of size $p$ is used for training a linear classifier over $n$ training samples. The classifier is obtained by running gradient-descent (GD) on the logistic-loss. For this model, we investigate the dependence of the generalization error on the overparameterization ratio $\kappa=p/n$. First, building on known deterministic results on convergence properties of the GD, we uncover a phase-transition phenomenon for the case of Gaussian regressors: the generalization error of GD is the same as that of the maximum-likelihood (ML) solution when $\kappa<\kappa_\star$, and that of the max-margin (SVM) solution when $\kappa>\kappa_\star$. Next, using the convex Gaussian min-max theorem (CGMT), we sharply characterize the performance of both the ML and SVM solutions. Combining these results, we obtain curves that explicitly characterize the generalization error of GD for varying values of $\kappa$. The numerical results validate the theoretical predictions and unveil double-descent phenomena that complement similar recent observations in linear regression settings.