Asymptotic Behavior of Multi--Task Learning: Implicit Regularization and Double Descent Effects

Multi--task learning seeks to improve the generalization error by leveraging the common information shared by multiple related tasks. One challenge in multi--task learning is identifying formulations capable of uncovering the common information shared between different but related tasks. This paper provides a precise asymptotic analysis of a popular multi--task formulation associated with misspecified perceptron learning models. The main contribution of this paper is to precisely determine the reasons behind the benefits gained from combining multiple related tasks. Specifically, we show that combining multiple tasks is asymptotically equivalent to a traditional formulation with additional regularization terms that help improve the generalization performance. Another contribution is to empirically study the impact of combining tasks on the generalization error. In particular, we empirically show that the combination of multiple tasks postpones the double descent phenomenon and can mitigate it asymptotically.

Sharp Analysis of RLS-based Digital Precoder with Limited PAPR in Massive MIMO

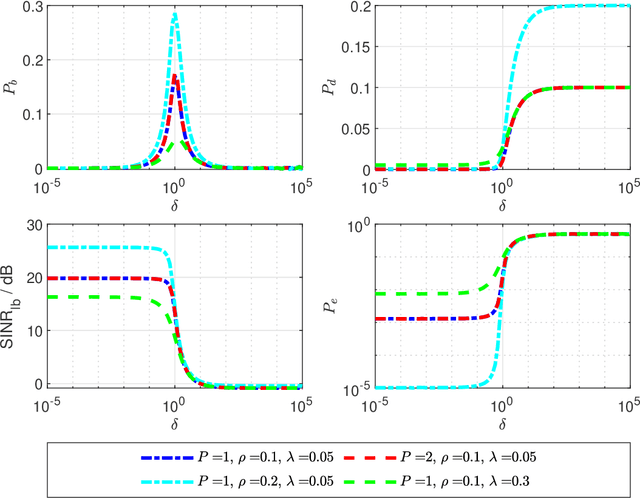
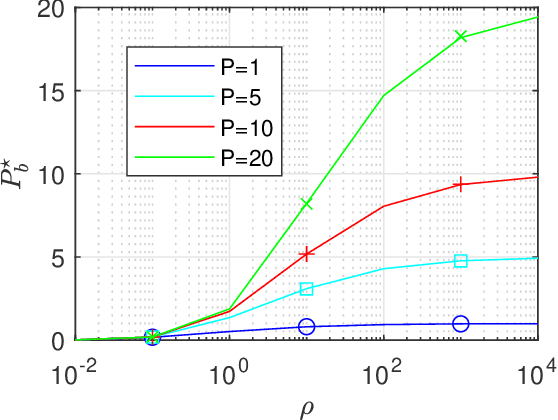
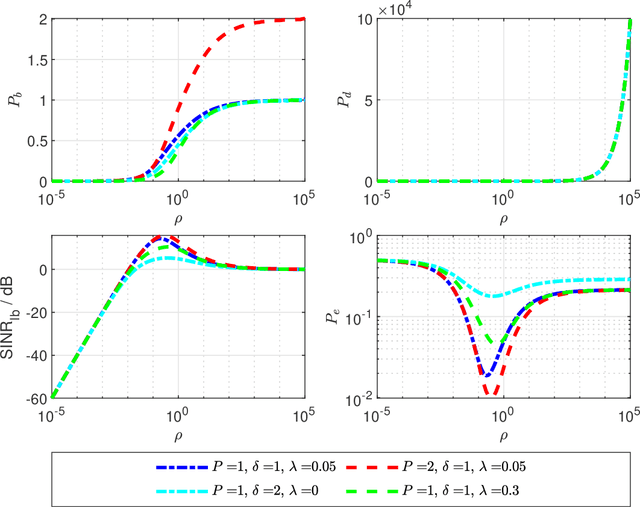
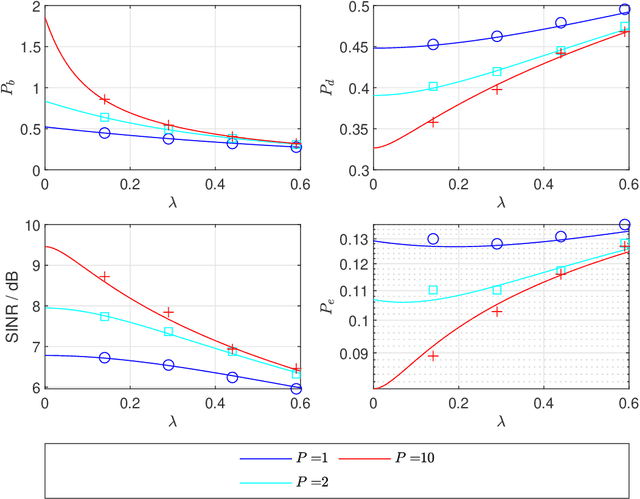
This paper focuses on the performance analysis of a class of limited peak-to-average power ratio (PAPR) precoders for downlink multi-user massive multiple-input multiple-output (MIMO) systems. Contrary to conventional precoding approaches based on simple linear precoders maximum ratio transmission (MRT) and regularized zero forcing (RZF), the precoders in this paper are obtained by solving a convex optimization problem. To be specific, for the precoders we analyze in this paper, the power of each precoded symbol entry is restricted, which allows them to present a reduced PAPR at each antenna. By using the Convex Gaussian Min-max Theorem (CGMT), we analytically characterize the empirical distribution of the precoded vector and the joint empirical distribution between the distortion and the intended symbol vector. This allows us to study the performance of these precoders in terms of per-antenna power, per-user distortion power, signal to interference and noise ratio, and bit error probability. We show that for this class of precoders, there is an optimal transmit power that maximizes the system performance.

Precise Performance Analysis of the Box-Elastic Net under Matrix Uncertainties

In this letter, we consider the problem of recovering an unknown sparse signal from noisy linear measurements, using an enhanced version of the popular Elastic-Net (EN) method. We modify the EN by adding a box-constraint, and we call it the Box-Elastic Net (Box-EN). We assume independent identically distributed (iid) real Gaussian measurement matrix with additive Gaussian noise. In many practical situations, the measurement matrix is not perfectly known, and so we only have a noisy estimate of it. In this work, we precisely characterize the mean squared error and the probability of support recovery of the Box-Elastic Net in the high-dimensional asymptotic regime. Numerical simulations validate the theoretical predictions derived in the paper and also show that the boxed variant outperforms the standard EN.