Weight Vector Tuning and Asymptotic Analysis of Binary Linear Classifiers

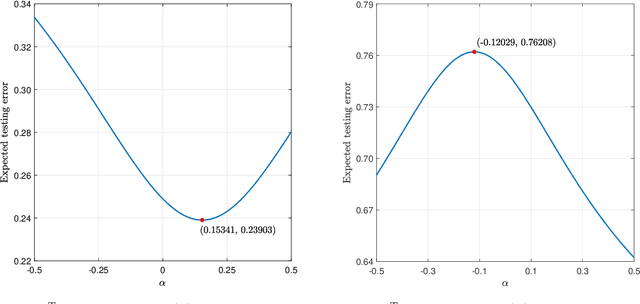
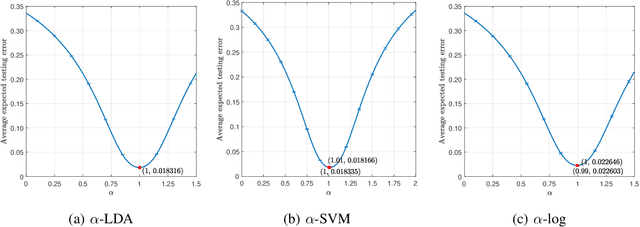
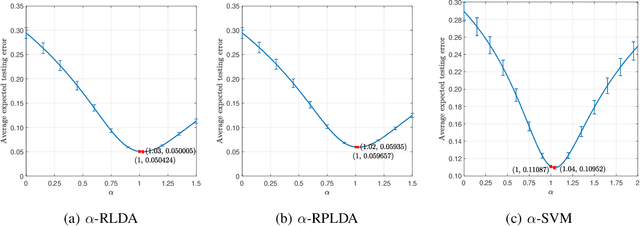
Unlike its intercept, a linear classifier's weight vector cannot be tuned by a simple grid search. Hence, this paper proposes weight vector tuning of a generic binary linear classifier through the parameterization of a decomposition of the discriminant by a scalar which controls the trade-off between conflicting informative and noisy terms. By varying this parameter, the original weight vector is modified in a meaningful way. Applying this method to a number of linear classifiers under a variety of data dimensionality and sample size settings reveals that the classification performance loss due to non-optimal native hyperparameters can be compensated for by weight vector tuning. This yields computational savings as the proposed tuning method reduces to tuning a scalar compared to tuning the native hyperparameter, which may involve repeated weight vector generation along with its burden of optimization, dimensionality reduction, etc., depending on the classifier. It is also found that weight vector tuning significantly improves the performance of Linear Discriminant Analysis (LDA) under high estimation noise. Proceeding from this second finding, an asymptotic study of the misclassification probability of the parameterized LDA classifier in the growth regime where the data dimensionality and sample size are comparable is conducted. Using random matrix theory, the misclassification probability is shown to converge to a quantity that is a function of the true statistics of the data. Additionally, an estimator of the misclassification probability is derived. Finally, computationally efficient tuning of the parameter using this estimator is demonstrated on real data.

Asymptotic Analysis of an Ensemble of Randomly Projected Linear Discriminants

Datasets from the fields of bioinformatics, chemometrics, and face recognition are typically characterized by small samples of high-dimensional data. Among the many variants of linear discriminant analysis that have been proposed in order to rectify the issues associated with classification in such a setting, the classifier in [1], composed of an ensemble of randomly projected linear discriminants, seems especially promising; it is computationally efficient and, with the optimal projection dimension parameter setting, is competitive with the state-of-the-art. In this work, we seek to further understand the behavior of this classifier through asymptotic analysis. Under the assumption of a growth regime in which the dataset and projection dimensions grow at constant rates to each other, we use random matrix theory to derive asymptotic misclassification probabilities showing the effect of the ensemble as a regularization of the data sample covariance matrix. The asymptotic errors further help to identify situations in which the ensemble offers a performance advantage. We also develop a consistent estimator of the misclassification probability as an alternative to the computationally-costly cross-validation estimator, which is conventionally used for parameter tuning. Finally, we demonstrate the use of our estimator for tuning the projection dimension on both real and synthetic data.