In-Context Reinforcement Learning From Suboptimal Historical Data

Transformer models have achieved remarkable empirical successes, largely due to their in-context learning capabilities. Inspired by this, we explore training an autoregressive transformer for in-context reinforcement learning (ICRL). In this setting, we initially train a transformer on an offline dataset consisting of trajectories collected from various RL tasks, and then fix and use this transformer to create an action policy for new RL tasks. Notably, we consider the setting where the offline dataset contains trajectories sampled from suboptimal behavioral policies. In this case, standard autoregressive training corresponds to imitation learning and results in suboptimal performance. To address this, we propose the Decision Importance Transformer(DIT) framework, which emulates the actor-critic algorithm in an in-context manner. In particular, we first train a transformer-based value function that estimates the advantage functions of the behavior policies that collected the suboptimal trajectories. Then we train a transformer-based policy via a weighted maximum likelihood estimation loss, where the weights are constructed based on the trained value function to steer the suboptimal policies to the optimal ones. We conduct extensive experiments to test the performance of DIT on both bandit and Markov Decision Process problems. Our results show that DIT achieves superior performance, particularly when the offline dataset contains suboptimal historical data.

Decoding Rewards in Competitive Games: Inverse Game Theory with Entropy Regularization

Estimating the unknown reward functions driving agents' behaviors is of central interest in inverse reinforcement learning and game theory. To tackle this problem, we develop a unified framework for reward function recovery in two-player zero-sum matrix games and Markov games with entropy regularization, where we aim to reconstruct the underlying reward functions given observed players' strategies and actions. This task is challenging due to the inherent ambiguity of inverse problems, the non-uniqueness of feasible rewards, and limited observational data coverage. To address these challenges, we establish the reward function's identifiability using the quantal response equilibrium (QRE) under linear assumptions. Building upon this theoretical foundation, we propose a novel algorithm to learn reward functions from observed actions. Our algorithm works in both static and dynamic settings and is adaptable to incorporate different methods, such as Maximum Likelihood Estimation (MLE). We provide strong theoretical guarantees for the reliability and sample efficiency of our algorithm. Further, we conduct extensive numerical studies to demonstrate the practical effectiveness of the proposed framework, offering new insights into decision-making in competitive environments.

Neuro-Logic Lifelong Learning

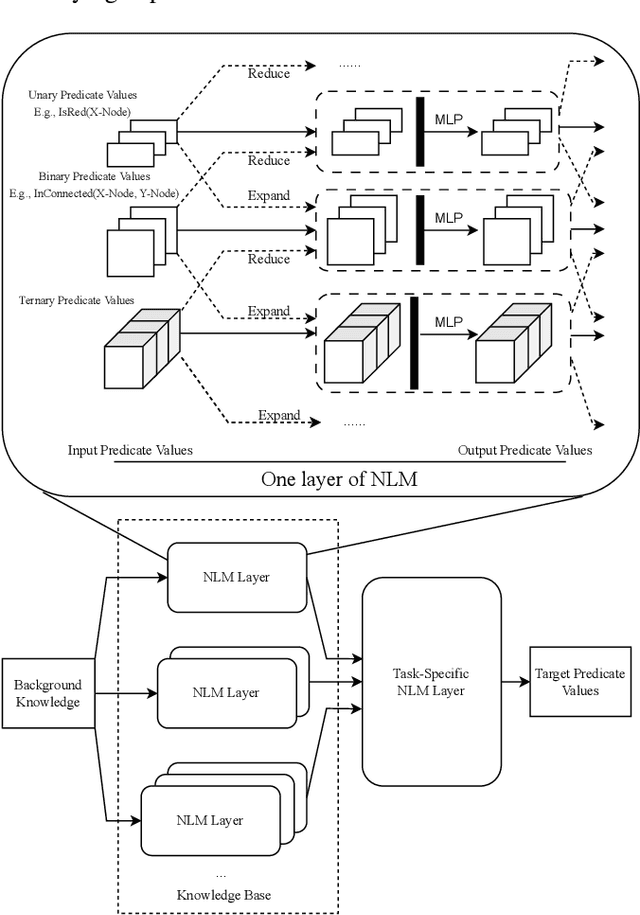
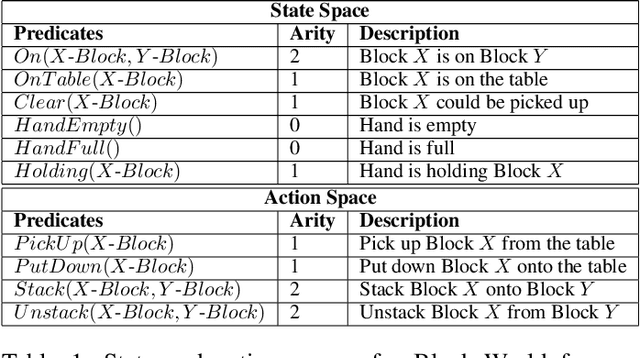
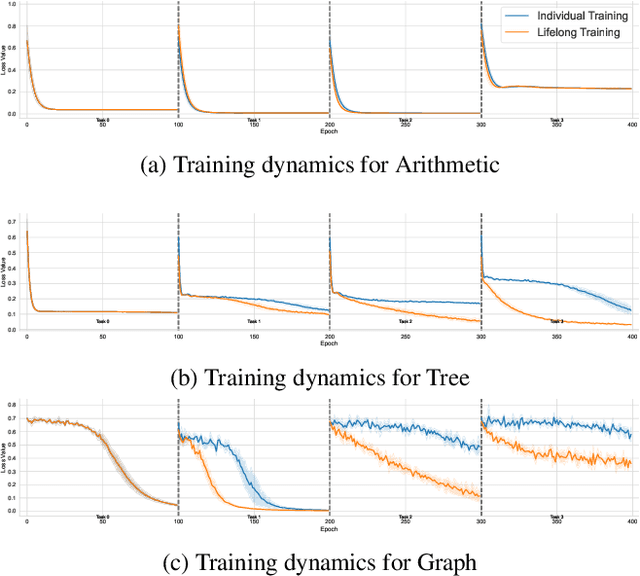
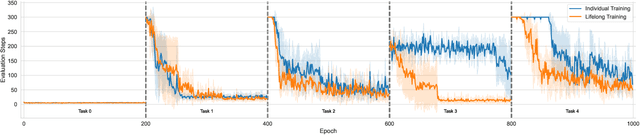
Solving Inductive Logic Programming (ILP) problems with neural networks is a key challenge in Neural-Symbolic Ar- tificial Intelligence (AI). While most research has focused on designing novel network architectures for individual prob- lems, less effort has been devoted to exploring new learning paradigms involving a sequence of problems. In this work, we investigate lifelong learning ILP, which leverages the com- positional and transferable nature of logic rules for efficient learning of new problems. We introduce a compositional framework, demonstrating how logic rules acquired from ear- lier tasks can be efficiently reused in subsequent ones, leading to improved scalability and performance. We formalize our approach and empirically evaluate it on sequences of tasks. Experimental results validate the feasibility and advantages of this paradigm, opening new directions for continual learn- ing in Neural-Symbolic AI.

Score-Based Quickest Change Detection and Fault Identification for Multi-Stream Signals

This paper introduces an approach to multi-stream quickest change detection and fault isolation for unnormalized and score-based statistical models. Traditional optimal algorithms in the quickest change detection literature require explicit pre-change and post-change distributions to calculate the likelihood ratio of the observations, which can be computationally expensive for higher-dimensional data and sometimes even infeasible for complex machine learning models. To address these challenges, we propose the min-SCUSUM method, a Hyvarinen score-based algorithm that computes the difference of score functions in place of log-likelihood ratios. We provide a delay and false alarm analysis of the proposed algorithm, showing that its asymptotic performance depends on the Fisher divergence between the pre- and post-change distributions. Furthermore, we establish an upper bound on the probability of fault misidentification in distinguishing the affected stream from the unaffected ones.

Conditional Score Learning for Quickest Change Detection in Markov Transition Kernels

We address the problem of quickest change detection in Markov processes with unknown transition kernels. The key idea is to learn the conditional score $\nabla_{\mathbf{y}} \log p(\mathbf{y}|\mathbf{x})$ directly from sample pairs $( \mathbf{x},\mathbf{y})$, where both $\mathbf{x}$ and $\mathbf{y}$ are high-dimensional data generated by the same transition kernel. In this way, we avoid explicit likelihood evaluation and provide a practical way to learn the transition dynamics. Based on this estimation, we develop a score-based CUSUM procedure that uses conditional Hyvarinen score differences to detect changes in the kernel. To ensure bounded increments, we propose a truncated version of the statistic. With Hoeffding's inequality for uniformly ergodic Markov processes, we prove exponential lower bounds on the mean time to false alarm. We also prove asymptotic upper bounds on detection delay. These results give both theoretical guarantees and practical feasibility for score-based detection in high-dimensional Markov models.

PASTA: A Unified Framework for Offline Assortment Learning

We study a broad class of assortment optimization problems in an offline and data-driven setting. In such problems, a firm lacks prior knowledge of the underlying choice model, and aims to determine an optimal assortment based on historical customer choice data. The combinatorial nature of assortment optimization often results in insufficient data coverage, posing a significant challenge in designing provably effective solutions. To address this, we introduce a novel Pessimistic Assortment Optimization (PASTA) framework that leverages the principle of pessimism to achieve optimal expected revenue under general choice models. Notably, PASTA requires only that the offline data distribution contains an optimal assortment, rather than providing the full coverage of all feasible assortments. Theoretically, we establish the first finite-sample regret bounds for offline assortment optimization across several widely used choice models, including the multinomial logit and nested logit models. Additionally, we derive a minimax regret lower bound, proving that PASTA is minimax optimal in terms of sample and model complexity. Numerical experiments further demonstrate that our method outperforms existing baseline approaches.

Dual-Function Radar-Communication Beamforming with Outage Probability Metric

The integrated design of communication and sensing may offer a potential solution to address spectrum congestion. In this work, we develop a beamforming method for a dual-function radar-communication system, where the transmit signal is used for both radar surveillance and communication with multiple downlink users, despite imperfect channel state information (CSI). We focus on two scenarios of interest: radar-centric and communication-centric. In the radar-centric scenario, the primary goal is to optimize radar performance while attaining acceptable communication performance. To this end, we minimize a weighted sum of the mean-squared error in achieving a desired beampattern and a mean-squared cross correlation of the radar returns from directions of interest (DOI). We also seek to ensure that the probability of outage for the communication users remains below a desired threshold. In the communication-centric scenario, our main objective is to minimize the maximum probability of outage among the communication users while keeping the aforementioned radar metrics below a desired threshold. Both optimization problems are stochastic and untractable. We first take advantage of central limit theorem to obtain deterministic non-convex problems and then consider relaxations of these problems in the form of semidefinite programs with rank-1 constraints. We provide numerical experiments demonstrating the effectiveness of the proposed designs.

Conditional Average Treatment Effect Estimation Under Hidden Confounders

One of the major challenges in estimating conditional potential outcomes and conditional average treatment effects (CATE) is the presence of hidden confounders. Since testing for hidden confounders cannot be accomplished only with observational data, conditional unconfoundedness is commonly assumed in the literature of CATE estimation. Nevertheless, under this assumption, CATE estimation can be significantly biased due to the effects of unobserved confounders. In this work, we consider the case where in addition to a potentially large observational dataset, a small dataset from a randomized controlled trial (RCT) is available. Notably, we make no assumptions on the existence of any covariate information for the RCT dataset, we only require the outcomes to be observed. We propose a CATE estimation method based on a pseudo-confounder generator and a CATE model that aligns the learned potential outcomes from the observational data with those observed from the RCT. Our method is applicable to many practical scenarios of interest, particularly those where privacy is a concern (e.g., medical applications). Extensive numerical experiments are provided demonstrating the effectiveness of our approach for both synthetic and real-world datasets.

Elliptic Loss Regularization

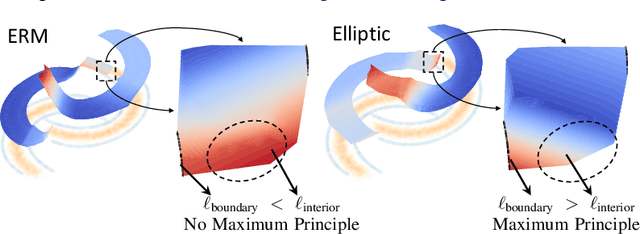
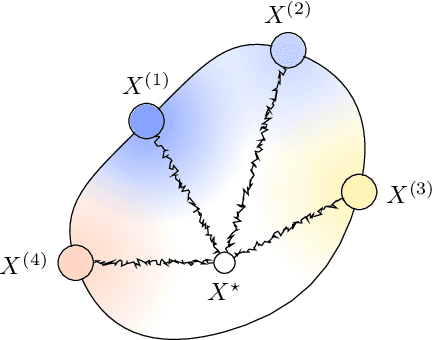
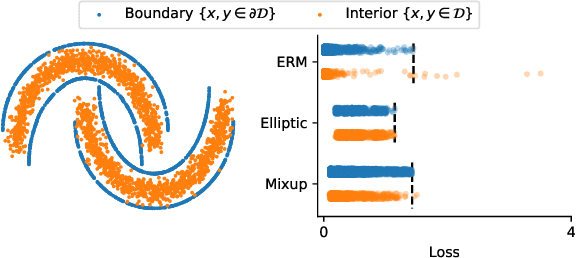
Regularizing neural networks is important for anticipating model behavior in regions of the data space that are not well represented. In this work, we propose a regularization technique for enforcing a level of smoothness in the mapping between the data input space and the loss value. We specify the level of regularity by requiring that the loss of the network satisfies an elliptic operator over the data domain. To do this, we modify the usual empirical risk minimization objective such that we instead minimize a new objective that satisfies an elliptic operator over points within the domain. This allows us to use existing theory on elliptic operators to anticipate the behavior of the error for points outside the training set. We propose a tractable computational method that approximates the behavior of the elliptic operator while being computationally efficient. Finally, we analyze the properties of the proposed regularization to understand the performance on common problems of distribution shift and group imbalance. Numerical experiments confirm the utility of the proposed regularization technique.

Parabolic Continual Learning

Regularizing continual learning techniques is important for anticipating algorithmic behavior under new realizations of data. We introduce a new approach to continual learning by imposing the properties of a parabolic partial differential equation (PDE) to regularize the expected behavior of the loss over time. This class of parabolic PDEs has a number of favorable properties that allow us to analyze the error incurred through forgetting and the error induced through generalization. Specifically, we do this through imposing boundary conditions where the boundary is given by a memory buffer. By using the memory buffer as a boundary, we can enforce long term dependencies by bounding the expected error by the boundary loss. Finally, we illustrate the empirical performance of the method on a series of continual learning tasks.