Offline Stochastic Optimization of Black-Box Objective Functions

Many challenges in science and engineering, such as drug discovery and communication network design, involve optimizing complex and expensive black-box functions across vast search spaces. Thus, it is essential to leverage existing data to avoid costly active queries of these black-box functions. To this end, while Offline Black-Box Optimization (BBO) is effective for deterministic problems, it may fall short in capturing the stochasticity of real-world scenarios. To address this, we introduce Stochastic Offline BBO (SOBBO), which tackles both black-box objectives and uncontrolled uncertainties. We propose two solutions: for large-data regimes, a differentiable surrogate allows for gradient-based optimization, while for scarce-data regimes, we directly estimate gradients under conservative field constraints, improving robustness, convergence, and data efficiency. Numerical experiments demonstrate the effectiveness of our approach on both synthetic and real-world tasks.

Steinmetz Neural Networks for Complex-Valued Data

In this work, we introduce a new approach to processing complex-valued data using DNNs consisting of parallel real-valued subnetworks with coupled outputs. Our proposed class of architectures, referred to as Steinmetz Neural Networks, leverages multi-view learning to construct more interpretable representations within the latent space. Subsequently, we present the Analytic Neural Network, which implements a consistency penalty that encourages analytic signal representations in the Steinmetz neural network's latent space. This penalty enforces a deterministic and orthogonal relationship between the real and imaginary components. Utilizing an information-theoretic construction, we demonstrate that the upper bound on the generalization error posited by the analytic neural network is lower than that of the general class of Steinmetz neural networks. Our numerical experiments demonstrate the improved performance and robustness to additive noise, afforded by our proposed networks on benchmark datasets and synthetic examples.

RASPNet: A Benchmark Dataset for Radar Adaptive Signal Processing Applications

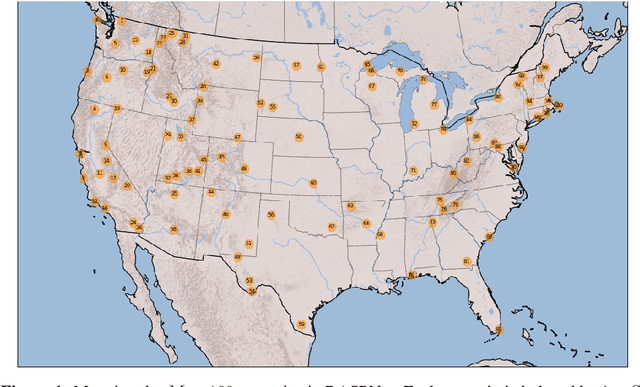
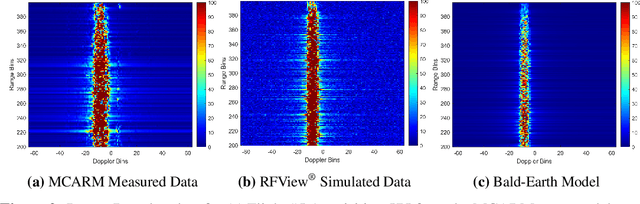
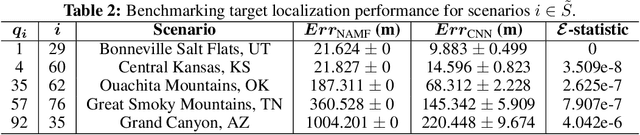
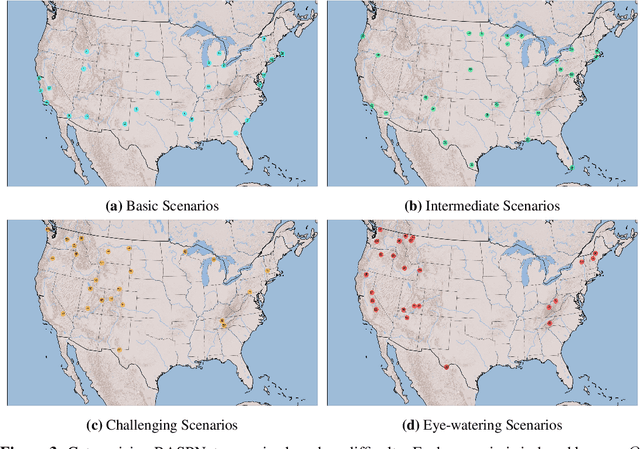
This work presents a large-scale dataset for radar adaptive signal processing (RASP) applications, aimed at supporting the development of data-driven models within the radar community. The dataset, called RASPNet, consists of 100 realistic scenarios compiled over a variety of topographies and land types from across the contiguous United States, designed to reflect a diverse array of real-world environments. Within each scenario, RASPNet consists of 10,000 clutter realizations from an airborne radar setting, which can be utilized for radar algorithm development and evaluation. RASPNet intends to fill a prominent gap in the availability of a large-scale, realistic dataset that standardizes the evaluation of adaptive radar processing techniques. We describe its construction, organization, and several potential applications, which includes a transfer learning example to demonstrate how RASPNet can be leveraged for realistic adaptive radar processing scenarios.

Data-Driven Target Localization: Benchmarking Gradient Descent Using the Cramér-Rao Bound

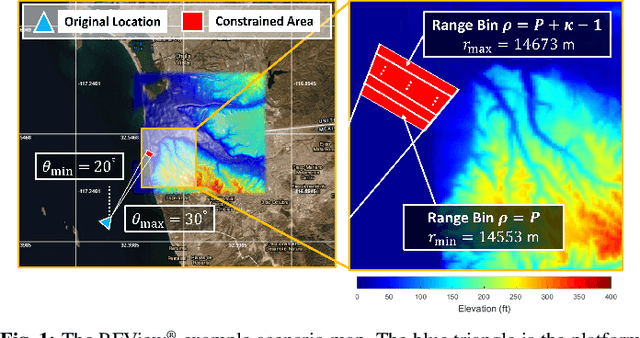
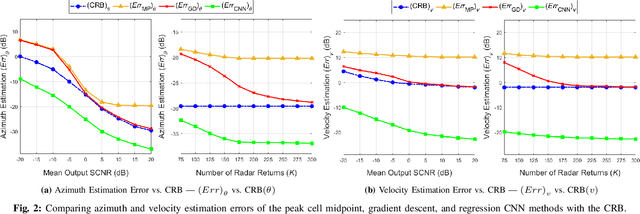
In modern radar systems, precise target localization using azimuth and velocity estimation is paramount. Traditional unbiased estimation methods have leveraged gradient descent algorithms to reach the theoretical limits of the Cram\'er Rao Bound (CRB) for the error of the parameter estimates. In this study, we present a data-driven neural network approach that outperforms these traditional techniques, demonstrating improved accuracies in target azimuth and velocity estimation. Using a representative simulated scenario, we show that our proposed neural network model consistently achieves improved parameter estimates due to its inherently biased nature, yielding a diminished mean squared error (MSE). Our findings underscore the potential of employing deep learning methods in radar systems, paving the way for more accurate localization in cluttered and dynamic environments.

Subspace Perturbation Analysis for Data-Driven Radar Target Localization

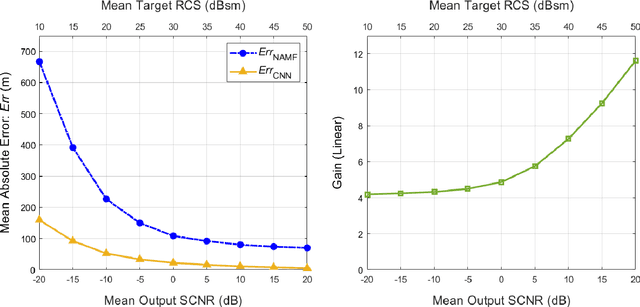
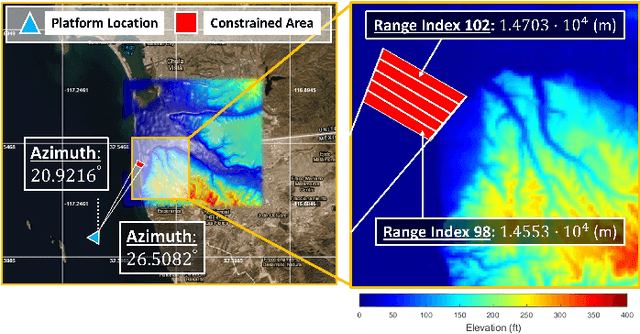
Recent works exploring data-driven approaches to classical problems in adaptive radar have demonstrated promising results pertaining to the task of radar target localization. Via the use of space-time adaptive processing (STAP) techniques and convolutional neural networks, these data-driven approaches to target localization have helped benchmark the performance of neural networks for matched scenarios. However, the thorough bridging of these topics across mismatched scenarios still remains an open problem. As such, in this work, we augment our data-driven approach to radar target localization by performing a subspace perturbation analysis, which allows us to benchmark the localization accuracy of our proposed deep learning framework across mismatched scenarios. To evaluate this framework, we generate comprehensive datasets by randomly placing targets of variable strengths in mismatched constrained areas via RFView, a high-fidelity, site-specific modeling and simulation tool. For the radar returns from these constrained areas, we generate heatmap tensors in range, azimuth, and elevation using the normalized adaptive matched filter (NAMF) test statistic. We estimate target locations from these heatmap tensors using a convolutional neural network, and demonstrate that the predictive performance of our framework in the presence of mismatches can be predetermined.

Minimax Concave Penalty Regularized Adaptive System Identification

We develop a recursive least square (RLS) type algorithm with a minimax concave penalty (MCP) for adaptive identification of a sparse tap-weight vector that represents a communication channel. The proposed algorithm recursively yields its estimate of the tap-vector, from noisy streaming observations of a received signal, using expectation-maximization (EM) update. We prove the convergence of our algorithm to a local optimum and provide bounds for the steady state error. Using simulation studies of Rayleigh fading channel, Volterra system and multivariate time series model, we demonstrate that our algorithm outperforms, in the mean-squared error (MSE) sense, the standard RLS and the $\ell_1$-regularized RLS.

Toward Data-Driven Radar STAP

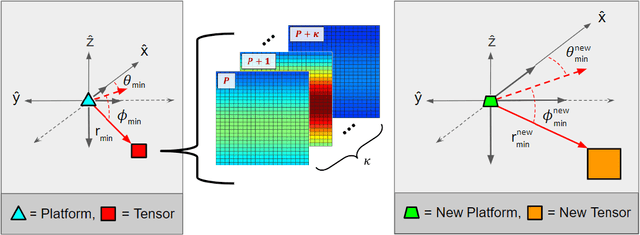
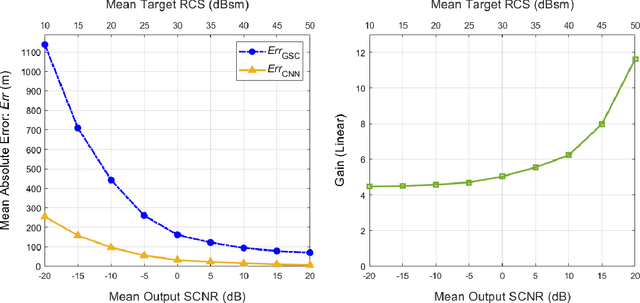
Catalyzed by the recent emergence of site-specific, high-fidelity radio frequency (RF) modeling and simulation tools purposed for radar, data-driven formulations of classical methods in radar have rapidly grown in popularity over the past decade. Despite this surge, limited focus has been directed toward the theoretical foundations of these classical methods. In this regard, as part of our ongoing data-driven approach to radar space-time adaptive processing (STAP), we analyze the asymptotic performance guarantees of select subspace separation methods in the context of radar target localization, and augment this analysis through a proposed deep learning framework for target location estimation. In our approach, we generate comprehensive datasets by randomly placing targets of variable strengths in predetermined constrained areas using RFView, a site-specific RF modeling and simulation tool developed by ISL Inc. For each radar return signal from these constrained areas, we generate heatmap tensors in range, azimuth, and elevation of the normalized adaptive matched filter (NAMF) test statistic, and of the output power of a generalized sidelobe canceller (GSC). Using our deep learning framework, we estimate target locations from these heatmap tensors to demonstrate the feasibility of and significant improvements provided by our data-driven approach in matched and mismatched settings.

Group-Theoretic Wideband Radar Waveform Design

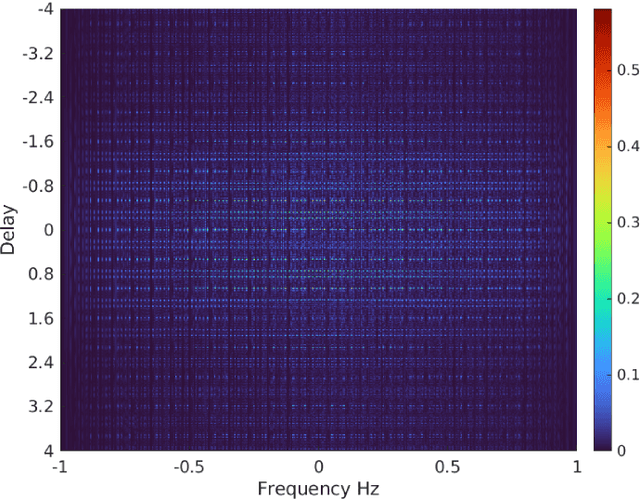
We investigate the theory of affine groups in the context of designing radar waveforms that obey the desired wideband ambiguity function (WAF). The WAF is obtained by correlating the signal with its time-dilated, Doppler-shifted, and delayed replicas. We consider the WAF definition as a coefficient function of the unitary representation of the group $a\cdot x + b$. This is essentially an algebraic problem applied to the radar waveform design. Prior works on this subject largely analyzed narrow-band ambiguity functions. Here, we show that when the underlying wideband signal of interest is a pulse or pulse train, a tight frame can be built to design that waveform. Specifically, we design the radar signals by minimizing the ratio of bounding constants of the frame in order to obtain lower sidelobes in the WAF. This minimization is performed by building a codebook based on difference sets in order to achieve the Welch bound. We show that the tight frame so obtained is connected with the wavelet transform that defines the WAF.

Toward Data-Driven STAP Radar

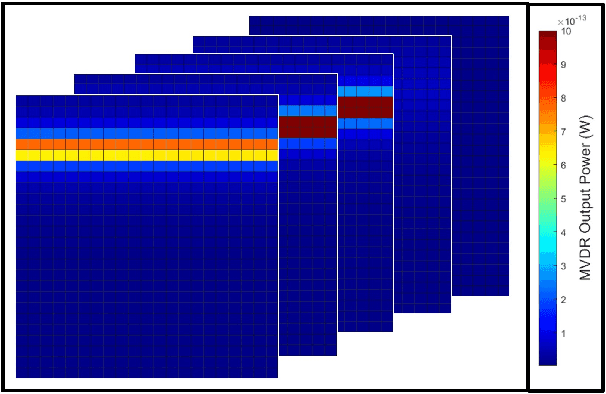
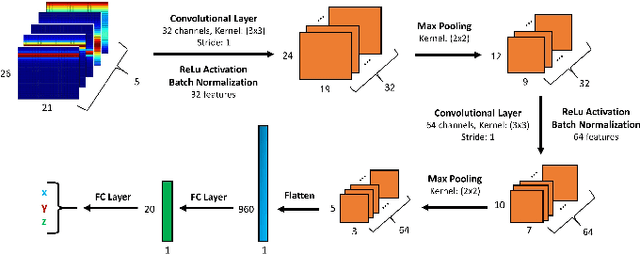
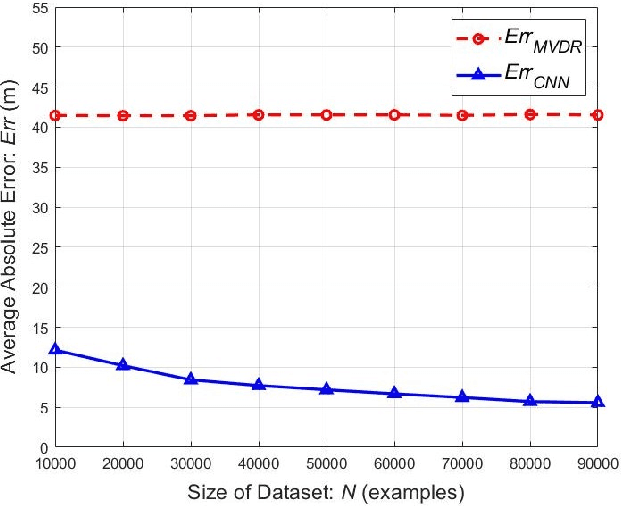
Using an amalgamation of techniques from classical radar, computer vision, and deep learning, we characterize our ongoing data-driven approach to space-time adaptive processing (STAP) radar. We generate a rich example dataset of received radar signals by randomly placing targets of variable strengths in a predetermined region using RFView, a site-specific radio frequency modeling and simulation tool developed by ISL Inc. For each data sample within this region, we generate heatmap tensors in range, azimuth, and elevation of the output power of a minimum variance distortionless response (MVDR) beamformer, which can be replaced with a desired test statistic. These heatmap tensors can be thought of as stacked images, and in an airborne scenario, the moving radar creates a sequence of these time-indexed image stacks, resembling a video. Our goal is to use these images and videos to detect targets and estimate their locations, a procedure reminiscent of computer vision algorithms for object detection$-$namely, the Faster Region-Based Convolutional Neural Network (Faster R-CNN). The Faster R-CNN consists of a proposal generating network for determining regions of interest (ROI), a regression network for positioning anchor boxes around targets, and an object classification algorithm; it is developed and optimized for natural images. Our ongoing research will develop analogous tools for heatmap images of radar data. In this regard, we will generate a large, representative adaptive radar signal processing database for training and testing, analogous in spirit to the COCO dataset for natural images. As a preliminary example, we present a regression network in this paper for estimating target locations to demonstrate the feasibility of and significant improvements provided by our data-driven approach.

Hypothesis Testing in Feedforward Networks with Broadcast Failures

Consider a countably infinite set of nodes, which sequentially make decisions between two given hypotheses. Each node takes a measurement of the underlying truth, observes the decisions from some immediate predecessors, and makes a decision between the given hypotheses. We consider two classes of broadcast failures: 1) each node broadcasts a decision to the other nodes, subject to random erasure in the form of a binary erasure channel; 2) each node broadcasts a randomly flipped decision to the other nodes in the form of a binary symmetric channel. We are interested in whether there exists a decision strategy consisting of a sequence of likelihood ratio tests such that the node decisions converge in probability to the underlying truth. In both cases, we show that if each node only learns from a bounded number of immediate predecessors, then there does not exist a decision strategy such that the decisions converge in probability to the underlying truth. However, in case 1, we show that if each node learns from an unboundedly growing number of predecessors, then the decisions converge in probability to the underlying truth, even when the erasure probabilities converge to 1. We also derive the convergence rate of the error probability. In case 2, we show that if each node learns from all of its previous predecessors, then the decisions converge in probability to the underlying truth when the flipping probabilities of the binary symmetric channels are bounded away from 1/2. In the case where the flipping probabilities converge to 1/2, we derive a necessary condition on the convergence rate of the flipping probabilities such that the decisions still converge to the underlying truth. We also explicitly characterize the relationship between the convergence rate of the error probability and the convergence rate of the flipping probabilities.