On The Energy Statistics of Feature Maps in Pruning of Neural Networks with Skip-Connections

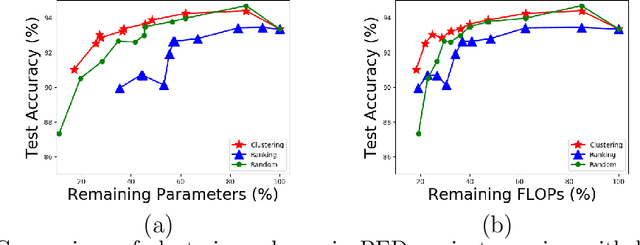
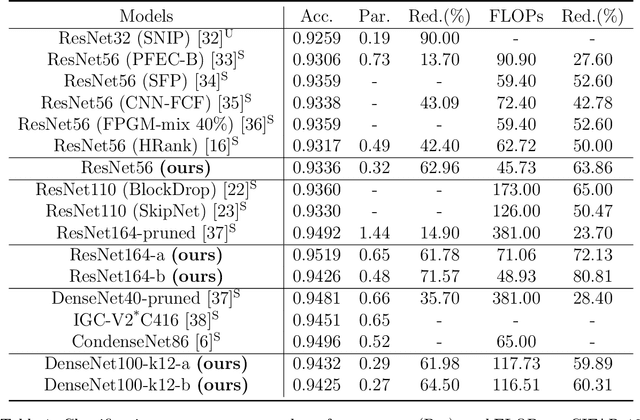
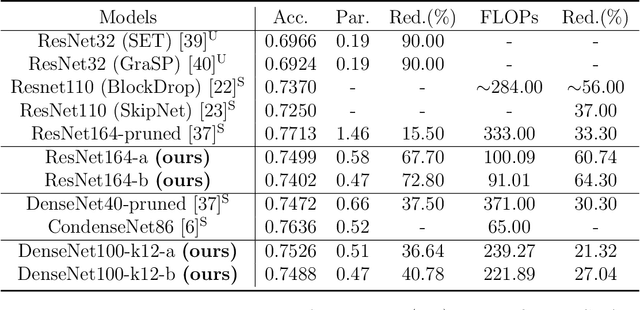
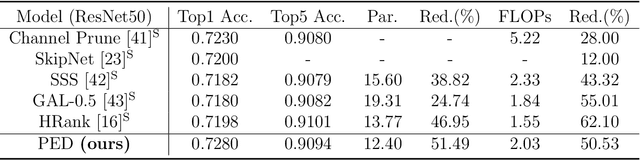
We propose a new structured pruning framework for compressing Deep Neural Networks (DNNs) with skip connections, based on measuring the statistical dependency of hidden layers and predicted outputs. The dependence measure defined by the energy statistics of hidden layers serves as a model-free measure of information between the feature maps and the output of the network. The estimated dependence measure is subsequently used to prune a collection of redundant and uninformative layers. Model-freeness of our measure guarantees that no parametric assumptions on the feature map distribution are required, making it computationally appealing for very high dimensional feature space in DNNs. Extensive numerical experiments on various architectures show the efficacy of the proposed pruning approach with competitive performance to state-of-the-art methods.

Toward Data-Driven STAP Radar

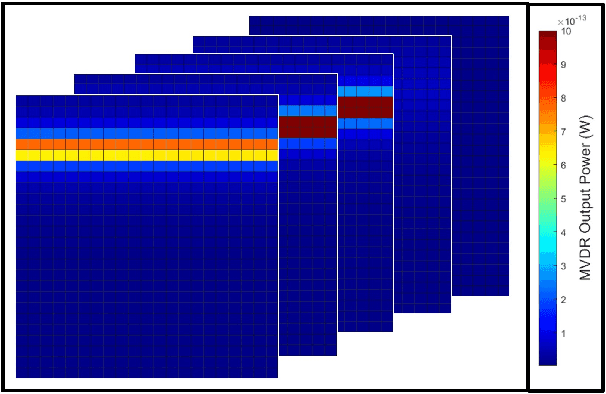
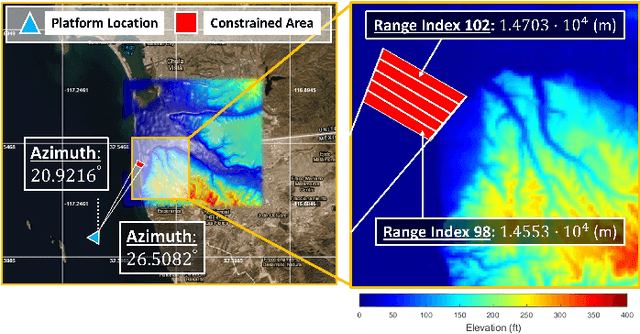
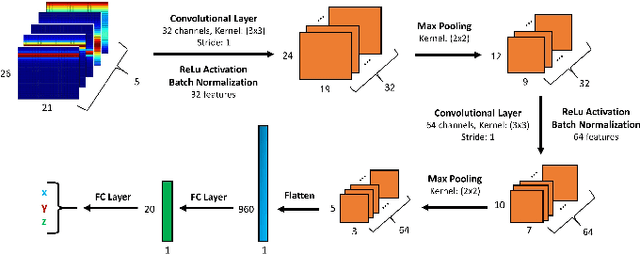
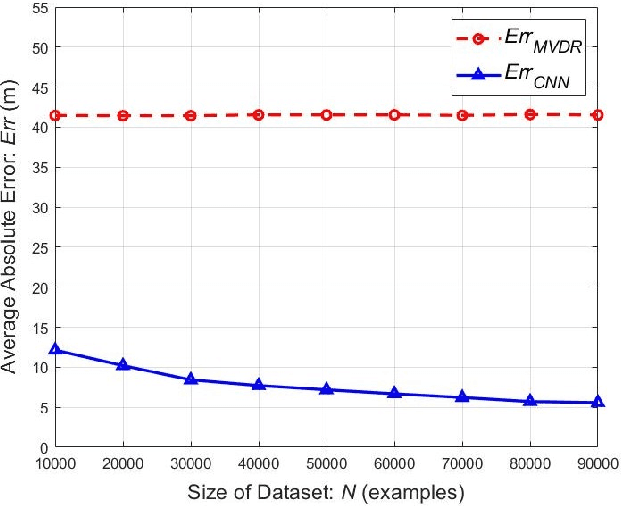
Using an amalgamation of techniques from classical radar, computer vision, and deep learning, we characterize our ongoing data-driven approach to space-time adaptive processing (STAP) radar. We generate a rich example dataset of received radar signals by randomly placing targets of variable strengths in a predetermined region using RFView, a site-specific radio frequency modeling and simulation tool developed by ISL Inc. For each data sample within this region, we generate heatmap tensors in range, azimuth, and elevation of the output power of a minimum variance distortionless response (MVDR) beamformer, which can be replaced with a desired test statistic. These heatmap tensors can be thought of as stacked images, and in an airborne scenario, the moving radar creates a sequence of these time-indexed image stacks, resembling a video. Our goal is to use these images and videos to detect targets and estimate their locations, a procedure reminiscent of computer vision algorithms for object detection$-$namely, the Faster Region-Based Convolutional Neural Network (Faster R-CNN). The Faster R-CNN consists of a proposal generating network for determining regions of interest (ROI), a regression network for positioning anchor boxes around targets, and an object classification algorithm; it is developed and optimized for natural images. Our ongoing research will develop analogous tools for heatmap images of radar data. In this regard, we will generate a large, representative adaptive radar signal processing database for training and testing, analogous in spirit to the COCO dataset for natural images. As a preliminary example, we present a regression network in this paper for estimating target locations to demonstrate the feasibility of and significant improvements provided by our data-driven approach.

Blaschke Product Neural Networks (BPNN): A Physics-Infused Neural Network for Phase Retrieval of Meromorphic Functions

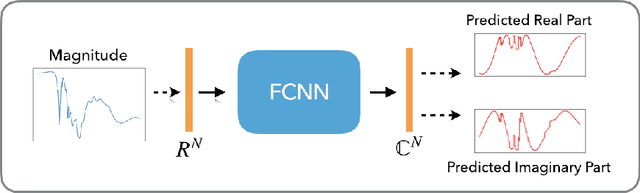
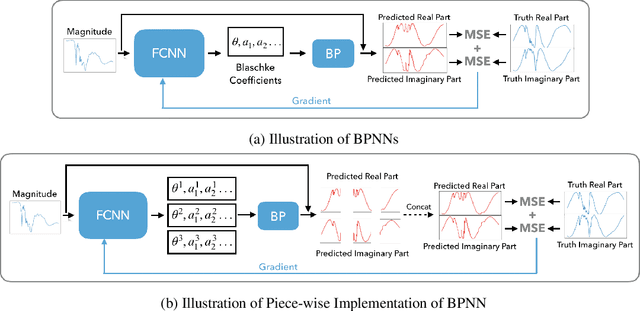
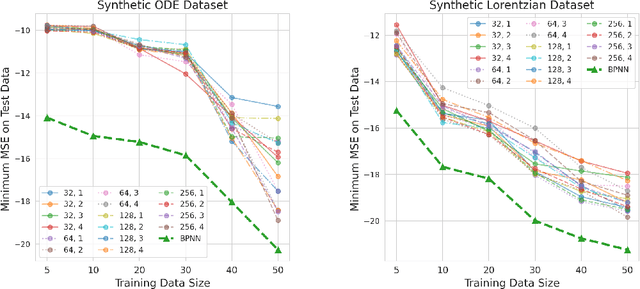
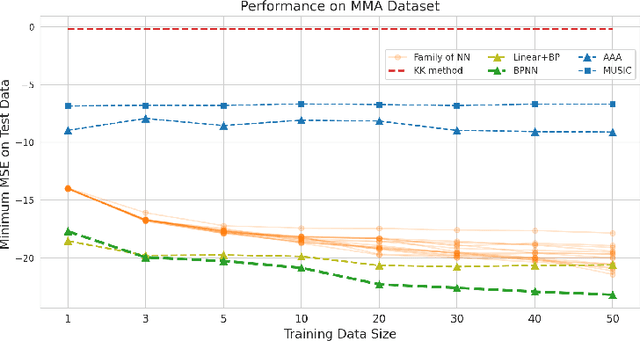
Numerous physical systems are described by ordinary or partial differential equations whose solutions are given by holomorphic or meromorphic functions in the complex domain. In many cases, only the magnitude of these functions are observed on various points on the purely imaginary jw-axis since coherent measurement of their phases is often expensive. However, it is desirable to retrieve the lost phases from the magnitudes when possible. To this end, we propose a physics-infused deep neural network based on the Blaschke products for phase retrieval. Inspired by the Helson and Sarason Theorem, we recover coefficients of a rational function of Blaschke products using a Blaschke Product Neural Network (BPNN), based upon the magnitude observations as input. The resulting rational function is then used for phase retrieval. We compare the BPNN to conventional deep neural networks (NNs) on several phase retrieval problems, comprising both synthetic and contemporary real-world problems (e.g., metamaterials for which data collection requires substantial expertise and is time consuming). On each phase retrieval problem, we compare against a population of conventional NNs of varying size and hyperparameter settings. Even without any hyper-parameter search, we find that BPNNs consistently outperform the population of optimized NNs in scarce data scenarios, and do so despite being much smaller models. The results can in turn be applied to calculate the refractive index of metamaterials, which is an important problem in emerging areas of material science.

Task Affinity with Maximum Bipartite Matching in Few-Shot Learning

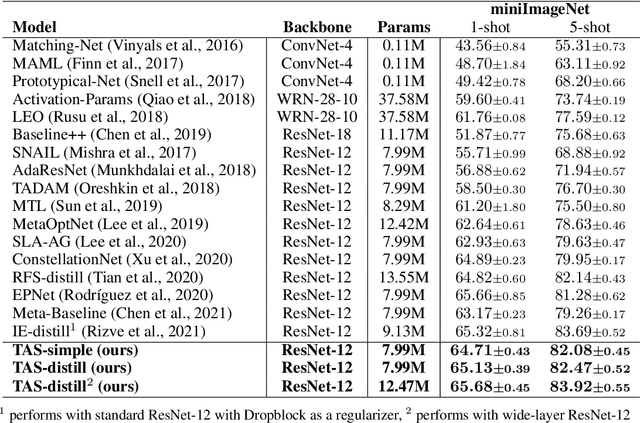
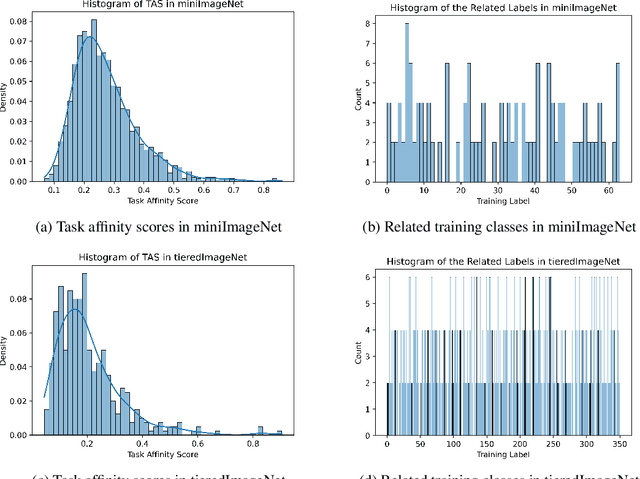
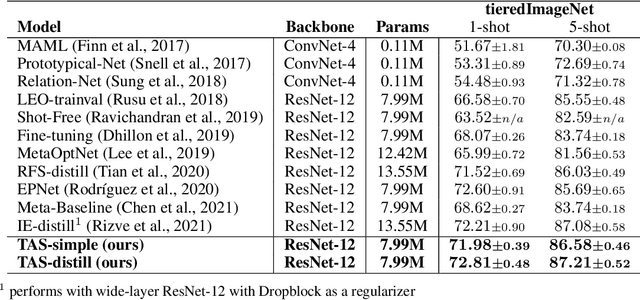
We propose an asymmetric affinity score for representing the complexity of utilizing the knowledge of one task for learning another one. Our method is based on the maximum bipartite matching algorithm and utilizes the Fisher Information matrix. We provide theoretical analyses demonstrating that the proposed score is mathematically well-defined, and subsequently use the affinity score to propose a novel algorithm for the few-shot learning problem. In particular, using this score, we find relevant training data labels to the test data and leverage the discovered relevant data for episodically fine-tuning a few-shot model. Results on various few-shot benchmark datasets demonstrate the efficacy of the proposed approach by improving the classification accuracy over the state-of-the-art methods even when using smaller models.

Towards Explainable Convolutional Features for Music Audio Modeling

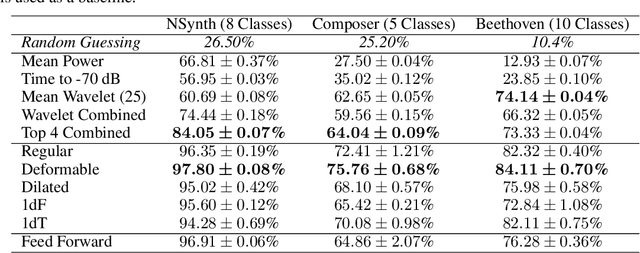
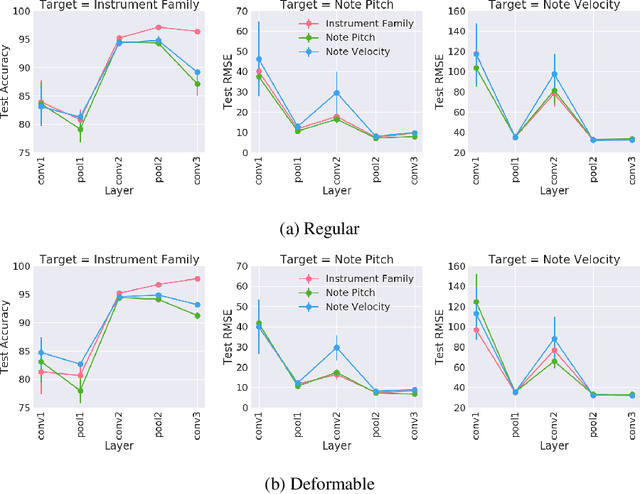
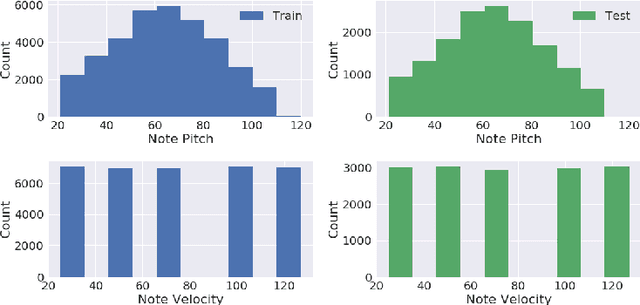
Audio signals are often represented as spectrograms and treated as 2D images. In this light, deep convolutional architectures are widely used for music audio tasks even though these two data types have very different structures. In this work, we attempt to "open the black-box" on deep convolutional models to inform future architectures for music audio tasks, and explain the excellent performance of deep convolutions that model spectrograms as 2D images. To this end, we expand recent explainability discussions in deep learning for natural image data to music audio data through systematic experiments using the deep features learned by various convolutional architectures. We demonstrate that deep convolutional features perform well across various target tasks, whether or not they are extracted from deep architectures originally trained on that task. Additionally, deep features exhibit high similarity to hand-crafted wavelet features, whether the deep features are extracted from a trained or untrained model.

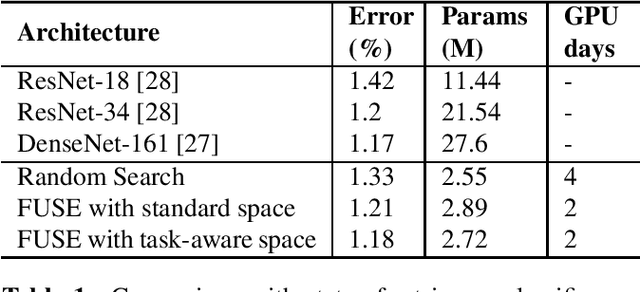
Neural Architecture Search From Fréchet Task Distance

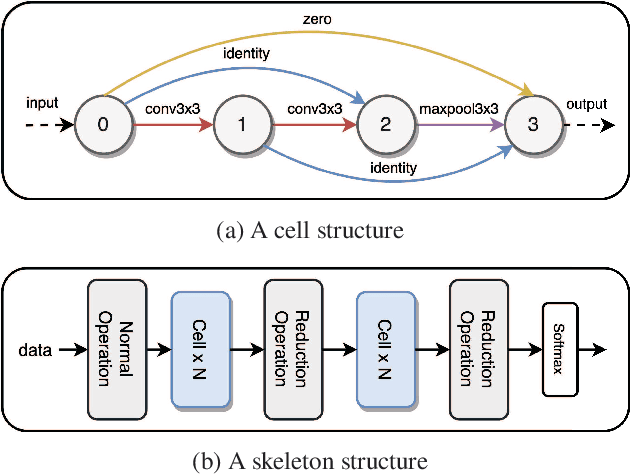
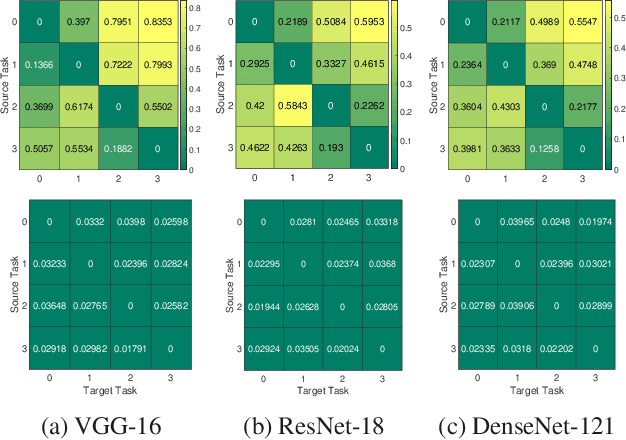
We formulate a Fr\'echet-type asymmetric distance between tasks based on Fisher Information Matrices. We show how the distance between a target task and each task in a given set of baseline tasks can be used to reduce the neural architecture search space for the target task. The complexity reduction in search space for task-specific architectures is achieved by building on the optimized architectures for similar tasks instead of doing a full search without using this side information. Experimental results demonstrate the efficacy of the proposed approach and its improvements over the state-of-the-art methods.

Neural Architecture Search From Task Similarity Measure

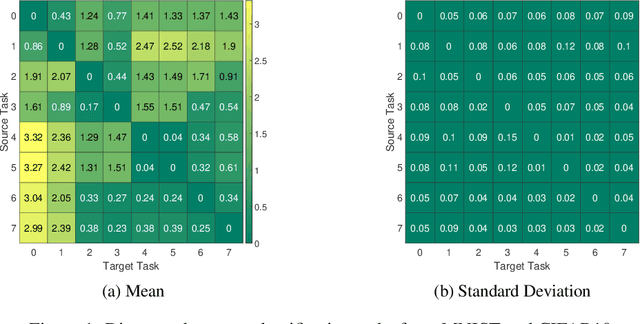
In this paper, we propose a neural architecture search framework based on a similarity measure between various tasks defined in terms of Fisher information. By utilizing the relation between a target and a set of existing tasks, the search space of architectures can be significantly reduced, making the discovery of the best candidates in the set of possible architectures tractable. This method eliminates the requirement for training the networks from scratch for the target task. Simulation results illustrate the efficacy of our proposed approach and its competitiveness with state-of-the-art methods.

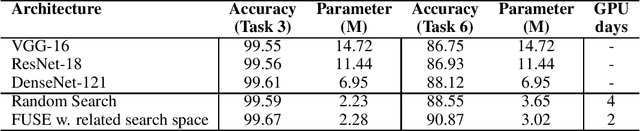
Task-Aware Neural Architecture Search

The design of handcrafted neural networks requires a lot of time and resources. Recent techniques in Neural Architecture Search (NAS) have proven to be competitive or better than traditional handcrafted design, although they require domain knowledge and have generally used limited search spaces. In this paper, we propose a novel framework for neural architecture search, utilizing a dictionary of models of base tasks and the similarity between the target task and the atoms of the dictionary; hence, generating an adaptive search space based on the base models of the dictionary. By introducing a gradient-based search algorithm, we can evaluate and discover the best architecture in the search space without fully training the networks. The experimental results show the efficacy of our proposed task-aware approach.

Projected Latent Markov Chain Monte Carlo: Conditional Inference with Normalizing Flows

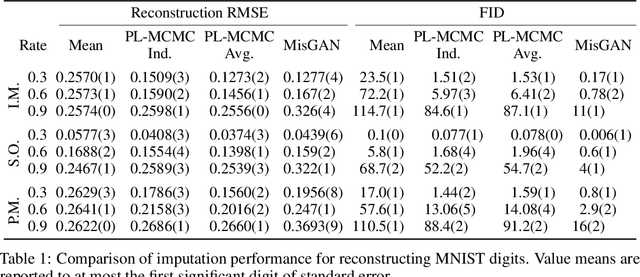
We introduce Projected Latent Markov Chain Monte Carlo (PL-MCMC), a technique for sampling from the high-dimensional conditional distributions learned by a normalizing flow. We prove that PL-MCMC asymptotically samples from the exact conditional distributions associated with a normalizing flow. As a conditional sampling method, PL-MCMC enables Monte Carlo Expectation Maximization (MC-EM) training of normalizing flows from incomplete data. By providing experimental results for a variety of data sets, we demonstrate the practicality and effectiveness of PL-MCMC for missing data inference using normalizing flows.

An Interpretable Baseline for Time Series Classification Without Intensive Learning

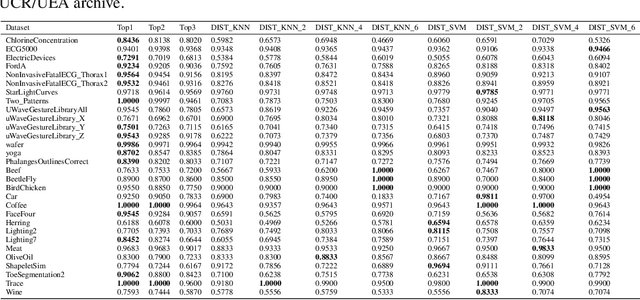
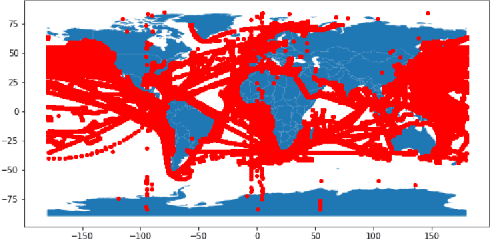
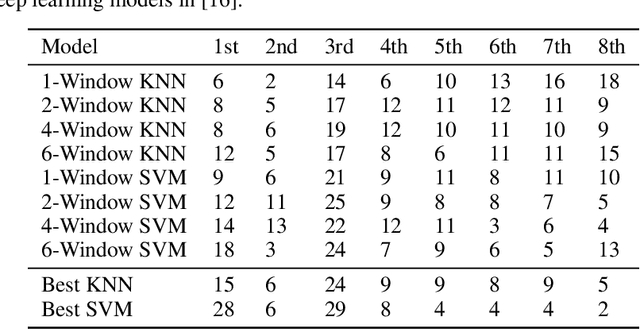
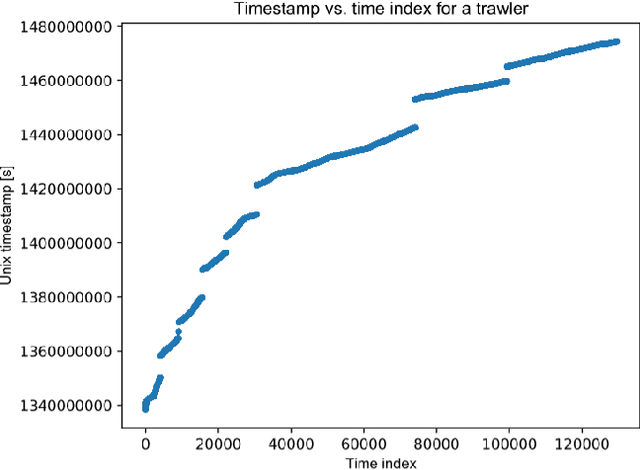
Recent advances in time series classification have largely focused on methods that either employ deep learning or utilize other machine learning models for feature extraction. Though such methods have proven powerful, they can also require computationally expensive models that may lack interpretability of results, or may require larger datasets than are freely available. In this paper, we propose an interpretable baseline based on representing each time series as a collection of probability distributions of extracted geometric features. The features used are intuitive and require minimal parameter tuning. We perform an exhaustive evaluation of our baseline on a large number of real datasets, showing that simple classifiers trained on these features exhibit surprising performance relative to state of the art methods requiring much more computational power. In particular, we show that our methodology achieves good performance on a challenging dataset involving the classification of fishing vessels, where our methods achieve good performance relative to the state of the art despite only having access to approximately two percent of the dataset used in training and evaluating this state of the art.