Predicting Next-Day Wildfire Spread with Time Series and Attention

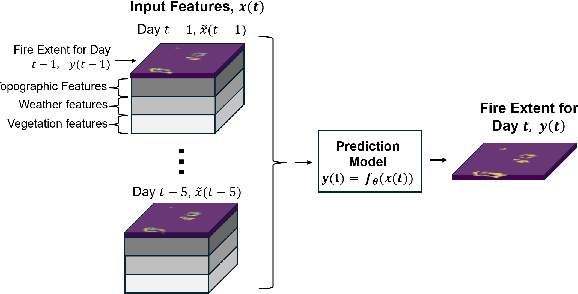
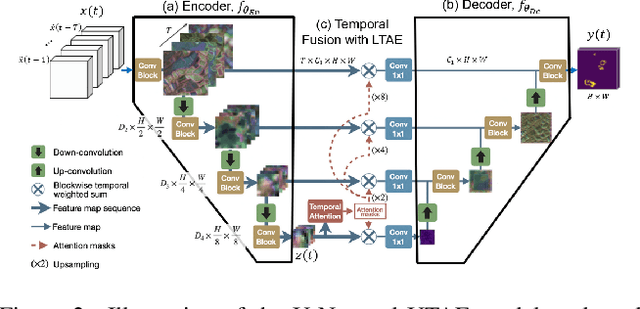
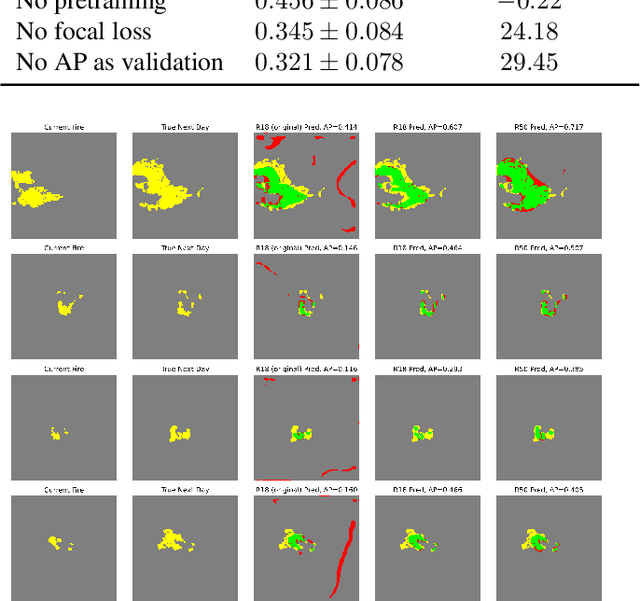
Recent research has demonstrated the potential of deep neural networks (DNNs) to accurately predict next-day wildfire spread, based upon the current extent of a fire and geospatial rasters of influential environmental covariates e.g., vegetation, topography, climate, and weather. In this work, we investigate a recent transformer-based model, termed the SwinUnet, for next-day wildfire prediction. We benchmark Swin-based models against several current state-of-the-art models on WildfireSpreadTS (WFTS), a large public benchmark dataset of historical wildfire events. We consider two next-day fire prediction scenarios: when the model is given input of (i) a single previous day of data, or (ii) five previous days of data. We find that, with the proper modifications, SwinUnet achieves state-of-the-art accuracy on next-day prediction for both the single-day and multi-day scenarios. SwinUnet's success depends heavily upon utilizing pre-trained weights from ImageNet. Consistent with prior work, we also found that models with multi-day-input always outperformed models with single-day input.

Deep Active Learning for Scientific Computing in the Wild

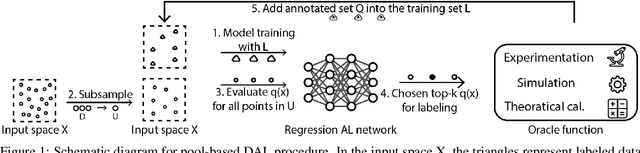
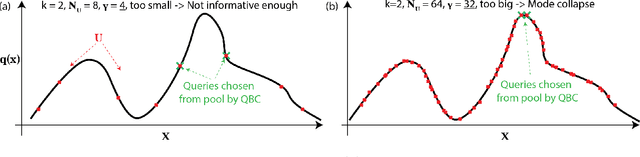
Deep learning (DL) is revolutionizing the scientific computing community. To reduce the data gap caused by usually expensive simulations or experimentation, active learning has been identified as a promising solution for the scientific computing community. However, the deep active learning (DAL) literature is currently dominated by image classification problems and pool-based methods, which are not directly transferrable to scientific computing problems, dominated by regression problems with no pre-defined 'pool' of unlabeled data. Here for the first time, we investigate the robustness of DAL methods for scientific computing problems using ten state-of-the-art DAL methods and eight benchmark problems. We show that, to our surprise, the majority of the DAL methods are not robust even compared to random sampling when the ideal pool size is unknown. We further analyze the effectiveness and robustness of DAL methods and suggest that diversity is necessary for a robust DAL for scientific computing problems.

Transformers For Recognition In Overhead Imagery: A Reality Check

There is evidence that transformers offer state-of-the-art recognition performance on tasks involving overhead imagery (e.g., satellite imagery). However, it is difficult to make unbiased empirical comparisons between competing deep learning models, making it unclear whether, and to what extent, transformer-based models are beneficial. In this paper we systematically compare the impact of adding transformer structures into state-of-the-art segmentation models for overhead imagery. Each model is given a similar budget of free parameters, and their hyperparameters are optimized using Bayesian Optimization with a fixed quantity of data and computation time. We conduct our experiments with a large and diverse dataset comprising two large public benchmarks: Inria and DeepGlobe. We perform additional ablation studies to explore the impact of specific transformer-based modeling choices. Our results suggest that transformers provide consistent, but modest, performance improvements. We only observe this advantage however in hybrid models that combine convolutional and transformer-based structures, while fully transformer-based models achieve relatively poor performance.

Hyperparameter-free deep active learning for regression problems via query synthesis

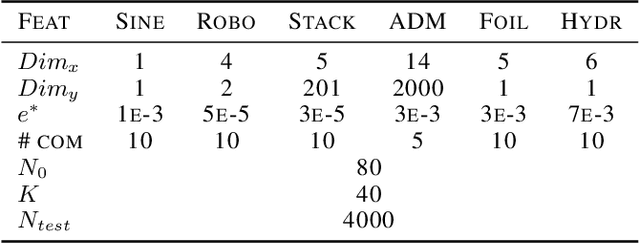
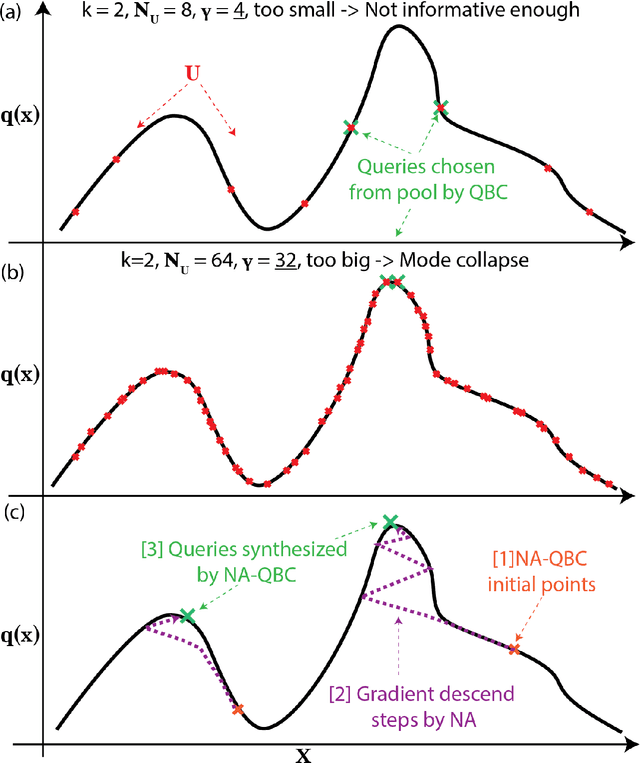
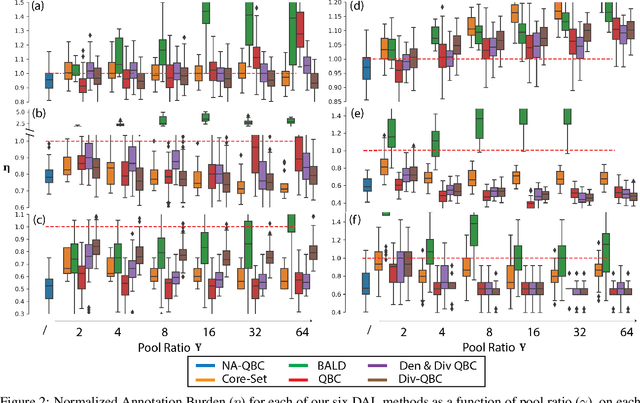
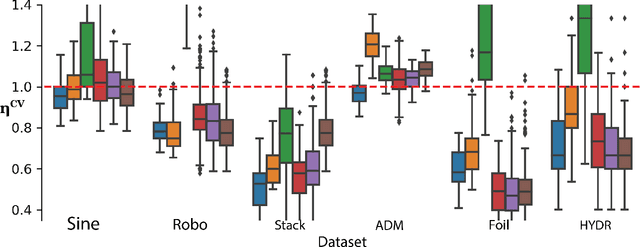
In the past decade, deep active learning (DAL) has heavily focused upon classification problems, or problems that have some 'valid' data manifolds, such as natural languages or images. As a result, existing DAL methods are not applicable to a wide variety of important problems -- such as many scientific computing problems -- that involve regression on relatively unstructured input spaces. In this work we propose the first DAL query-synthesis approach for regression problems. We frame query synthesis as an inverse problem and use the recently-proposed neural-adjoint (NA) solver to efficiently find points in the continuous input domain that optimize the query-by-committee (QBC) criterion. Crucially, the resulting NA-QBC approach removes the one sensitive hyperparameter of the classical QBC active learning approach - the "pool size"- making NA-QBC effectively hyperparameter free. This is significant because DAL methods can be detrimental, even compared to random sampling, if the wrong hyperparameters are chosen. We evaluate Random, QBC and NA-QBC sampling strategies on four regression problems, including two contemporary scientific computing problems. We find that NA-QBC achieves better average performance than random sampling on every benchmark problem, while QBC can be detrimental if the wrong hyperparameters are chosen.

Utilizing geospatial data for assessing energy security: Mapping small solar home systems using unmanned aerial vehicles and deep learning

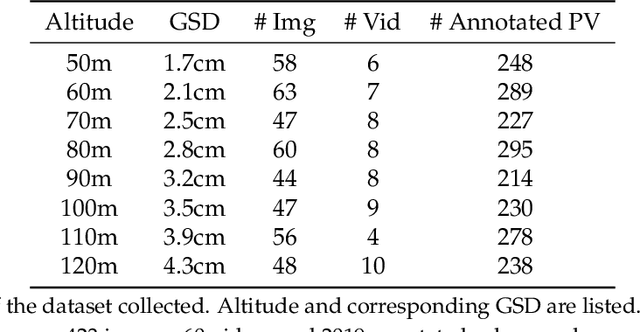
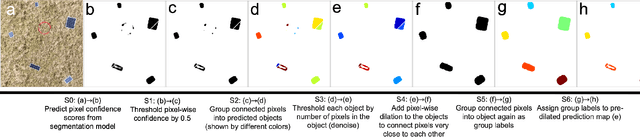
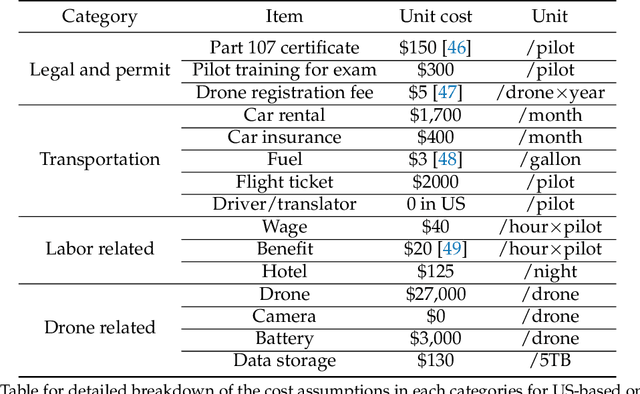
Solar home systems (SHS), a cost-effective solution for rural communities far from the grid in developing countries, are small solar panels and associated equipment that provides power to a single household. A crucial resource for targeting further investment of public and private resources, as well as tracking the progress of universal electrification goals, is shared access to high-quality data on individual SHS installations including information such as location and power capacity. Though recent studies utilizing satellite imagery and machine learning to detect solar panels have emerged, they struggle to accurately locate many SHS due to limited image resolution (some small solar panels only occupy several pixels in satellite imagery). In this work, we explore the viability and cost-performance tradeoff of using automatic SHS detection on unmanned aerial vehicle (UAV) imagery as an alternative to satellite imagery. More specifically, we explore three questions: (i) what is the detection performance of SHS using drone imagery; (ii) how expensive is the drone data collection, compared to satellite imagery; and (iii) how well does drone-based SHS detection perform in real-world scenarios. We collect and publicly-release a dataset of high-resolution drone imagery encompassing SHS imaged under real-world conditions and use this dataset and a dataset from Rwanda to evaluate the capabilities of deep learning models to recognize SHS, including those that are too small to be reliably recognized in satellite imagery. The results suggest that UAV imagery may be a viable alternative to identify very small SHS from perspectives of both detection accuracy and financial costs of data collection. UAV-based data collection may be a practical option for supporting electricity access planning strategies for achieving sustainable development goals and for monitoring the progress towards those goals.

Blaschke Product Neural Networks (BPNN): A Physics-Infused Neural Network for Phase Retrieval of Meromorphic Functions

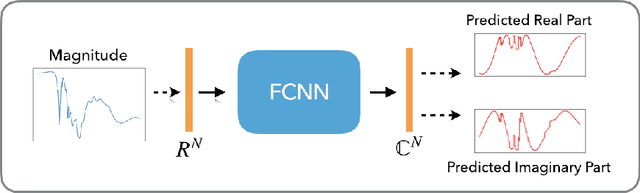
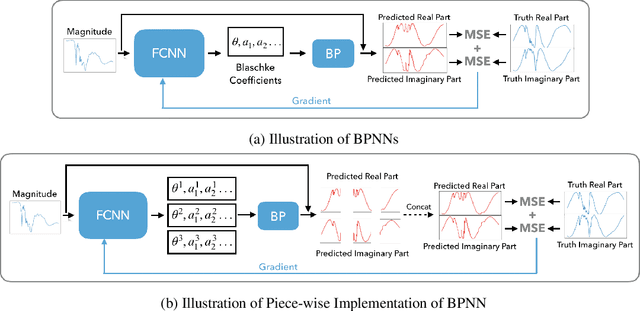
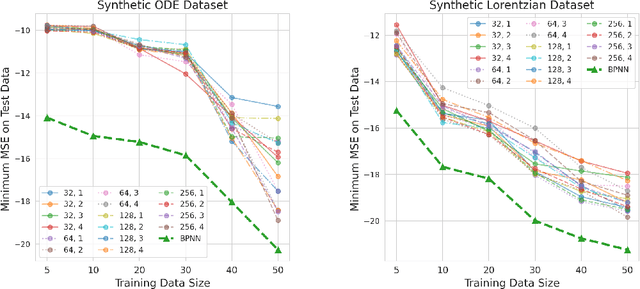
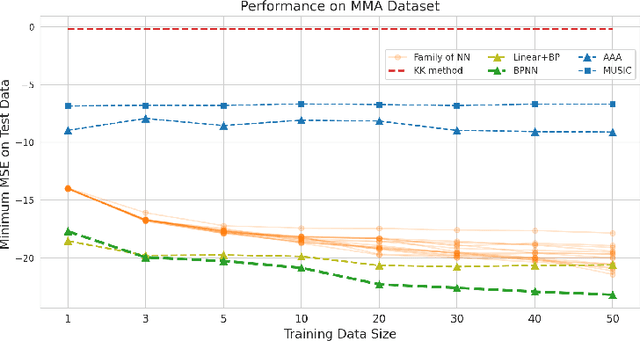
Numerous physical systems are described by ordinary or partial differential equations whose solutions are given by holomorphic or meromorphic functions in the complex domain. In many cases, only the magnitude of these functions are observed on various points on the purely imaginary jw-axis since coherent measurement of their phases is often expensive. However, it is desirable to retrieve the lost phases from the magnitudes when possible. To this end, we propose a physics-infused deep neural network based on the Blaschke products for phase retrieval. Inspired by the Helson and Sarason Theorem, we recover coefficients of a rational function of Blaschke products using a Blaschke Product Neural Network (BPNN), based upon the magnitude observations as input. The resulting rational function is then used for phase retrieval. We compare the BPNN to conventional deep neural networks (NNs) on several phase retrieval problems, comprising both synthetic and contemporary real-world problems (e.g., metamaterials for which data collection requires substantial expertise and is time consuming). On each phase retrieval problem, we compare against a population of conventional NNs of varying size and hyperparameter settings. Even without any hyper-parameter search, we find that BPNNs consistently outperform the population of optimized NNs in scarce data scenarios, and do so despite being much smaller models. The results can in turn be applied to calculate the refractive index of metamaterials, which is an important problem in emerging areas of material science.

GridTracer: Automatic Mapping of Power Grids using Deep Learning and Overhead Imagery

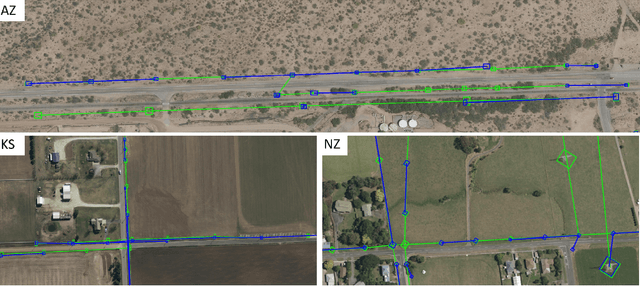
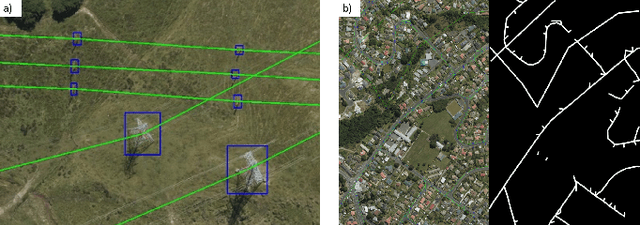
Energy system information valuable for electricity access planning such as the locations and connectivity of electricity transmission and distribution towers, termed the power grid, is often incomplete, outdated, or altogether unavailable. Furthermore, conventional means for collecting this information is costly and limited. We propose to automatically map the grid in overhead remotely sensed imagery using deep learning. Towards this goal, we develop and publicly-release a large dataset ($263km^2$) of overhead imagery with ground truth for the power grid, to our knowledge this is the first dataset of its kind in the public domain. Additionally, we propose scoring metrics and baseline algorithms for two grid mapping tasks: (1) tower recognition and (2) power line interconnection (i.e., estimating a graph representation of the grid). We hope the availability of the training data, scoring metrics, and baselines will facilitate rapid progress on this important problem to help decision-makers address the energy needs of societies around the world.

Benchmarking deep inverse models over time, and the neural-adjoint method

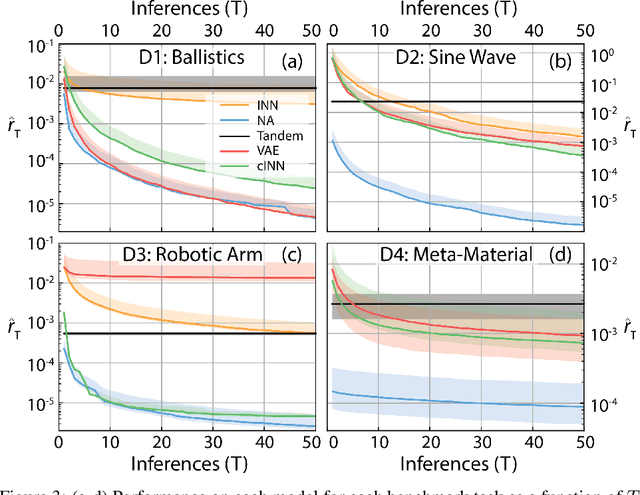
We consider the task of solving generic inverse problems, where one wishes to determine the hidden parameters of a natural system that will give rise to a particular set of measurements. Recently many new approaches based upon deep learning have arisen generating impressive results. We conceptualize these models as different schemes for efficiently, but randomly, exploring the space of possible inverse solutions. As a result, the accuracy of each approach should be evaluated as a function of time rather than a single estimated solution, as is often done now. Using this metric, we compare several state-of-the-art inverse modeling approaches on four benchmark tasks: two existing tasks, one simple task for visualization and one new task from metamaterial design. Finally, inspired by our conception of the inverse problem, we explore a solution that uses a deep learning model to approximate the forward model, and then uses backpropagation to search for good inverse solutions. This approach, termed the neural-adjoint, achieves the best performance in many scenarios.