Inverse deep learning methods and benchmarks for artificial electromagnetic material design

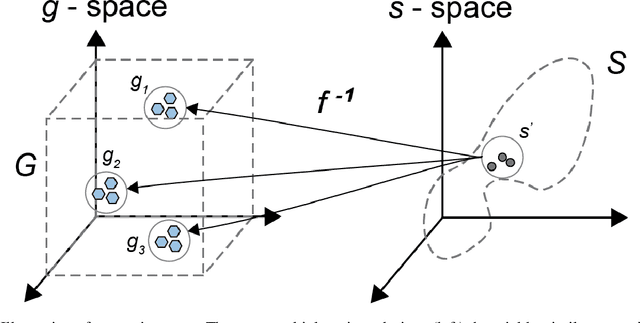
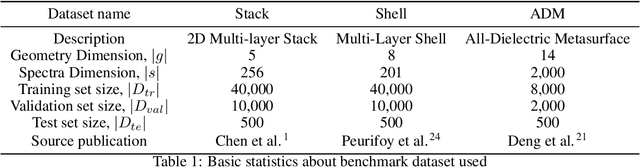
Deep learning (DL) inverse techniques have increased the speed of artificial electromagnetic material (AEM) design and improved the quality of resulting devices. Many DL inverse techniques have succeeded on a number of AEM design tasks, but to compare, contrast, and evaluate assorted techniques it is critical to clarify the underlying ill-posedness of inverse problems. Here we review state-of-the-art approaches and present a comprehensive survey of deep learning inverse methods and invertible and conditional invertible neural networks to AEM design. We produce easily accessible and rapidly implementable AEM design benchmarks, which offers a methodology to efficiently determine the DL technique best suited to solving different design challenges. Our methodology is guided by constraints on repeated simulation and an easily integrated metric, which we propose expresses the relative ill-posedness of any AEM design problem. We show that as the problem becomes increasingly ill-posed, the neural adjoint with boundary loss (NA) generates better solutions faster, regardless of simulation constraints. On simpler AEM design tasks, direct neural networks (NN) fare better when simulations are limited, while geometries predicted by mixture density networks (MDN) and conditional variational auto-encoders (VAE) can improve with continued sampling and re-simulation.

Blaschke Product Neural Networks (BPNN): A Physics-Infused Neural Network for Phase Retrieval of Meromorphic Functions

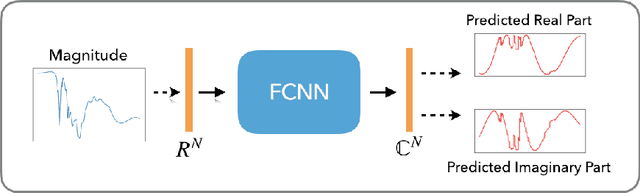
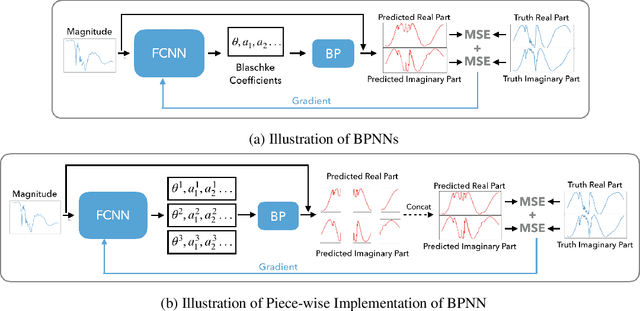
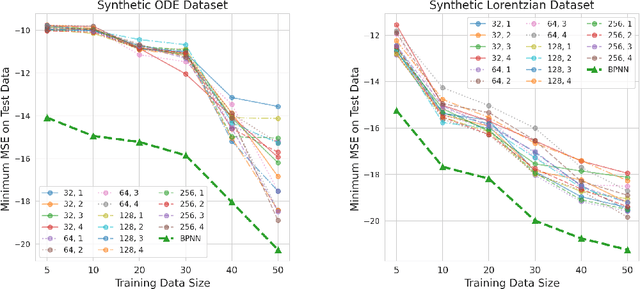
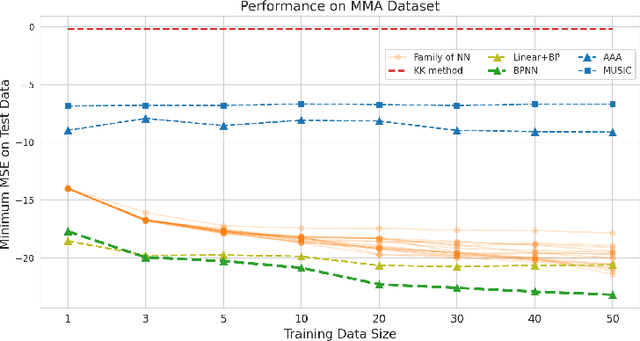
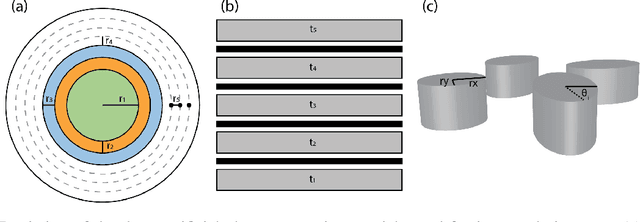
Numerous physical systems are described by ordinary or partial differential equations whose solutions are given by holomorphic or meromorphic functions in the complex domain. In many cases, only the magnitude of these functions are observed on various points on the purely imaginary jw-axis since coherent measurement of their phases is often expensive. However, it is desirable to retrieve the lost phases from the magnitudes when possible. To this end, we propose a physics-infused deep neural network based on the Blaschke products for phase retrieval. Inspired by the Helson and Sarason Theorem, we recover coefficients of a rational function of Blaschke products using a Blaschke Product Neural Network (BPNN), based upon the magnitude observations as input. The resulting rational function is then used for phase retrieval. We compare the BPNN to conventional deep neural networks (NNs) on several phase retrieval problems, comprising both synthetic and contemporary real-world problems (e.g., metamaterials for which data collection requires substantial expertise and is time consuming). On each phase retrieval problem, we compare against a population of conventional NNs of varying size and hyperparameter settings. Even without any hyper-parameter search, we find that BPNNs consistently outperform the population of optimized NNs in scarce data scenarios, and do so despite being much smaller models. The results can in turn be applied to calculate the refractive index of metamaterials, which is an important problem in emerging areas of material science.