Can Large Language Models Learn the Physics of Metamaterials? An Empirical Study with ChatGPT

Large language models (LLMs) such as ChatGPT, Gemini, LlaMa, and Claude are trained on massive quantities of text parsed from the internet and have shown a remarkable ability to respond to complex prompts in a manner often indistinguishable from humans. We present a LLM fine-tuned on up to 40,000 data that can predict electromagnetic spectra over a range of frequencies given a text prompt that only specifies the metasurface geometry. Results are compared to conventional machine learning approaches including feed-forward neural networks, random forest, linear regression, and K-nearest neighbor (KNN). Remarkably, the fine-tuned LLM (FT-LLM) achieves a lower error across all dataset sizes explored compared to all machine learning approaches including a deep neural network. We also demonstrate the LLM's ability to solve inverse problems by providing the geometry necessary to achieve a desired spectrum. LLMs possess some advantages over humans that may give them benefits for research, including the ability to process enormous amounts of data, find hidden patterns in data, and operate in higher-dimensional spaces. We propose that fine-tuning LLMs on large datasets specific to a field allows them to grasp the nuances of that domain, making them valuable tools for research and analysis.

Deep Active Learning for Scientific Computing in the Wild

Deep learning (DL) is revolutionizing the scientific computing community. To reduce the data gap caused by usually expensive simulations or experimentation, active learning has been identified as a promising solution for the scientific computing community. However, the deep active learning (DAL) literature is currently dominated by image classification problems and pool-based methods, which are not directly transferrable to scientific computing problems, dominated by regression problems with no pre-defined 'pool' of unlabeled data. Here for the first time, we investigate the robustness of DAL methods for scientific computing problems using ten state-of-the-art DAL methods and eight benchmark problems. We show that, to our surprise, the majority of the DAL methods are not robust even compared to random sampling when the ideal pool size is unknown. We further analyze the effectiveness and robustness of DAL methods and suggest that diversity is necessary for a robust DAL for scientific computing problems.

Hyperparameter-free deep active learning for regression problems via query synthesis

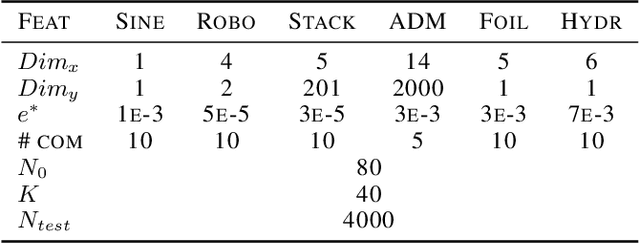
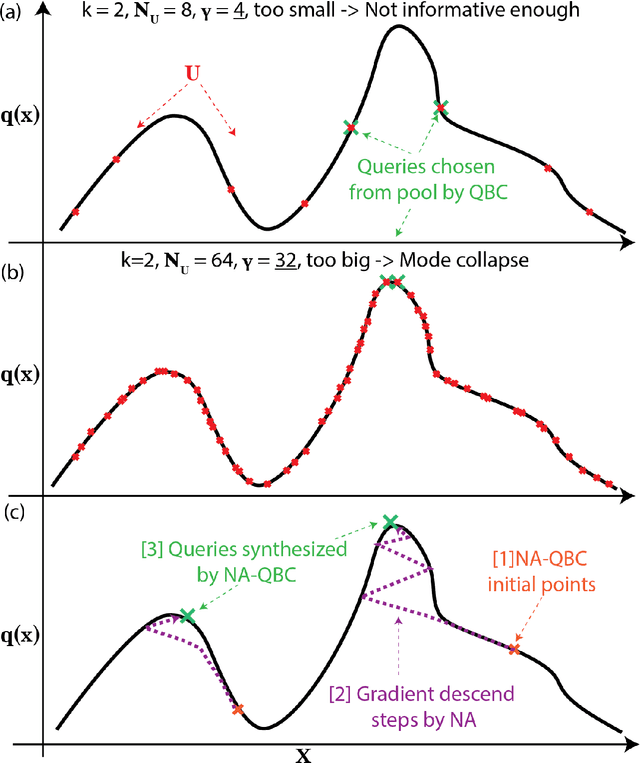
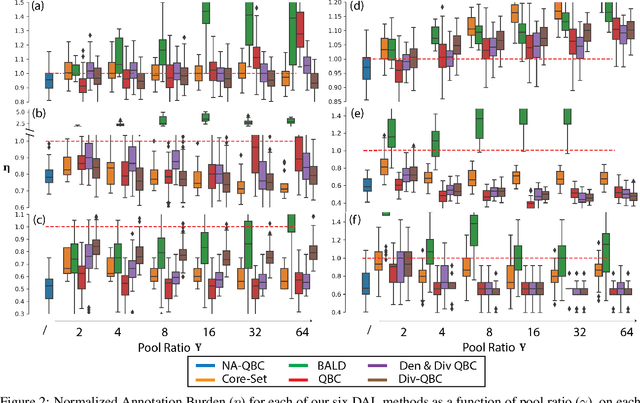
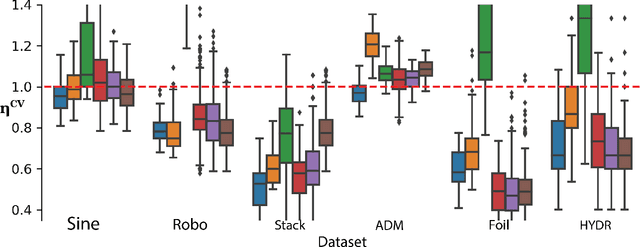
In the past decade, deep active learning (DAL) has heavily focused upon classification problems, or problems that have some 'valid' data manifolds, such as natural languages or images. As a result, existing DAL methods are not applicable to a wide variety of important problems -- such as many scientific computing problems -- that involve regression on relatively unstructured input spaces. In this work we propose the first DAL query-synthesis approach for regression problems. We frame query synthesis as an inverse problem and use the recently-proposed neural-adjoint (NA) solver to efficiently find points in the continuous input domain that optimize the query-by-committee (QBC) criterion. Crucially, the resulting NA-QBC approach removes the one sensitive hyperparameter of the classical QBC active learning approach - the "pool size"- making NA-QBC effectively hyperparameter free. This is significant because DAL methods can be detrimental, even compared to random sampling, if the wrong hyperparameters are chosen. We evaluate Random, QBC and NA-QBC sampling strategies on four regression problems, including two contemporary scientific computing problems. We find that NA-QBC achieves better average performance than random sampling on every benchmark problem, while QBC can be detrimental if the wrong hyperparameters are chosen.

Inverse deep learning methods and benchmarks for artificial electromagnetic material design

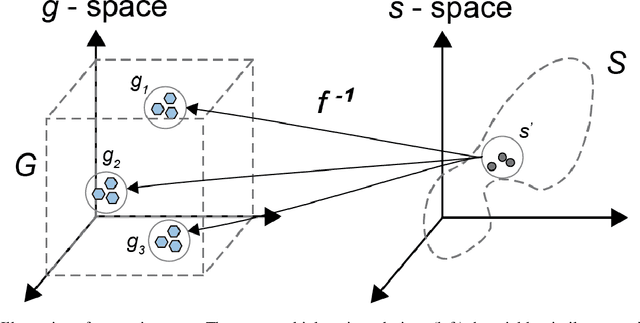
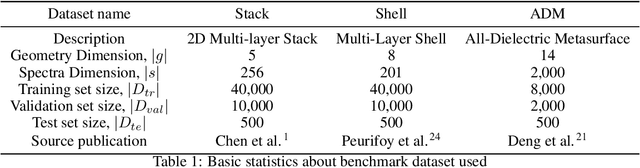
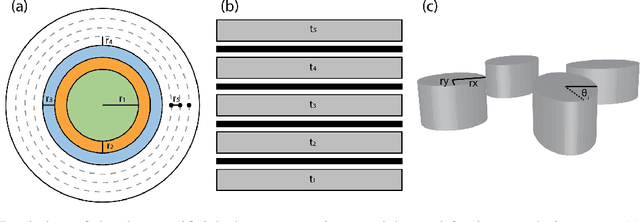
Deep learning (DL) inverse techniques have increased the speed of artificial electromagnetic material (AEM) design and improved the quality of resulting devices. Many DL inverse techniques have succeeded on a number of AEM design tasks, but to compare, contrast, and evaluate assorted techniques it is critical to clarify the underlying ill-posedness of inverse problems. Here we review state-of-the-art approaches and present a comprehensive survey of deep learning inverse methods and invertible and conditional invertible neural networks to AEM design. We produce easily accessible and rapidly implementable AEM design benchmarks, which offers a methodology to efficiently determine the DL technique best suited to solving different design challenges. Our methodology is guided by constraints on repeated simulation and an easily integrated metric, which we propose expresses the relative ill-posedness of any AEM design problem. We show that as the problem becomes increasingly ill-posed, the neural adjoint with boundary loss (NA) generates better solutions faster, regardless of simulation constraints. On simpler AEM design tasks, direct neural networks (NN) fare better when simulations are limited, while geometries predicted by mixture density networks (MDN) and conditional variational auto-encoders (VAE) can improve with continued sampling and re-simulation.