Hyperparameter-free deep active learning for regression problems via query synthesis

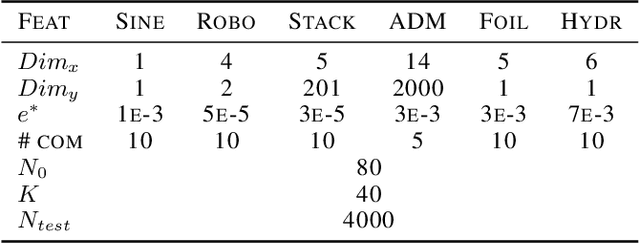
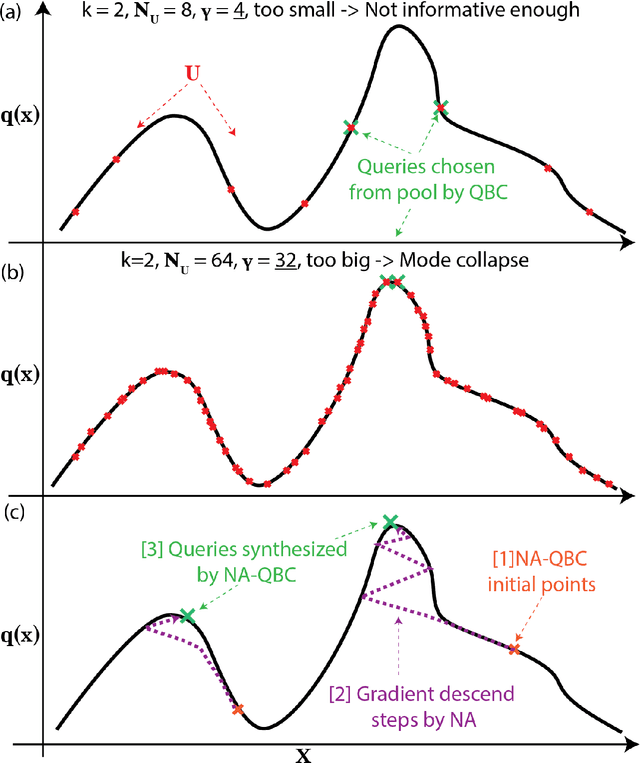
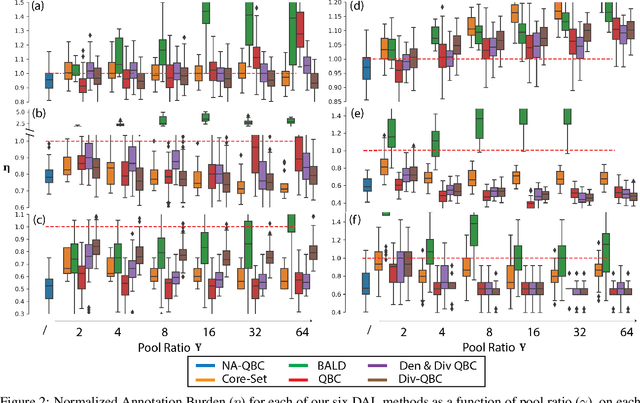
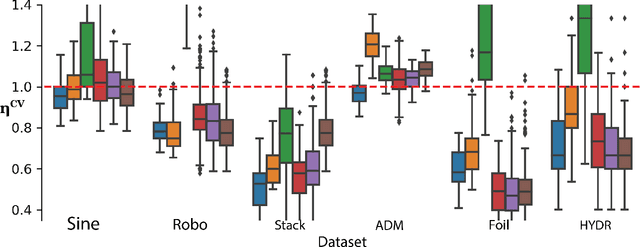
In the past decade, deep active learning (DAL) has heavily focused upon classification problems, or problems that have some 'valid' data manifolds, such as natural languages or images. As a result, existing DAL methods are not applicable to a wide variety of important problems -- such as many scientific computing problems -- that involve regression on relatively unstructured input spaces. In this work we propose the first DAL query-synthesis approach for regression problems. We frame query synthesis as an inverse problem and use the recently-proposed neural-adjoint (NA) solver to efficiently find points in the continuous input domain that optimize the query-by-committee (QBC) criterion. Crucially, the resulting NA-QBC approach removes the one sensitive hyperparameter of the classical QBC active learning approach - the "pool size"- making NA-QBC effectively hyperparameter free. This is significant because DAL methods can be detrimental, even compared to random sampling, if the wrong hyperparameters are chosen. We evaluate Random, QBC and NA-QBC sampling strategies on four regression problems, including two contemporary scientific computing problems. We find that NA-QBC achieves better average performance than random sampling on every benchmark problem, while QBC can be detrimental if the wrong hyperparameters are chosen.