Towards Explainable Convolutional Features for Music Audio Modeling

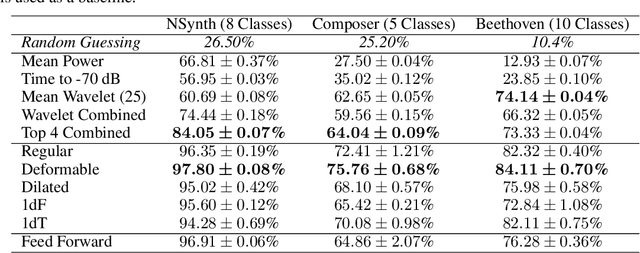
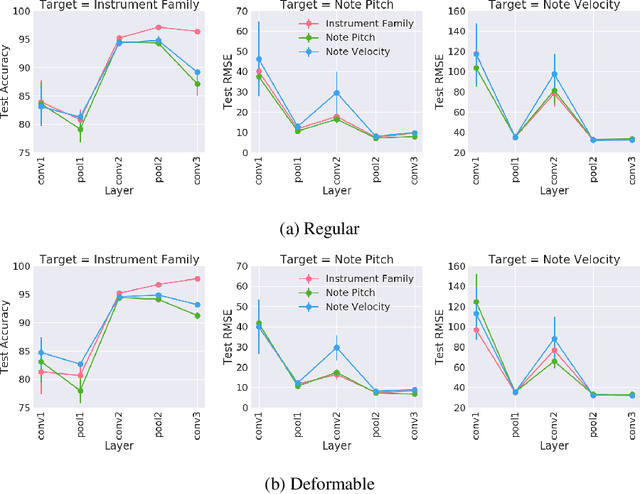
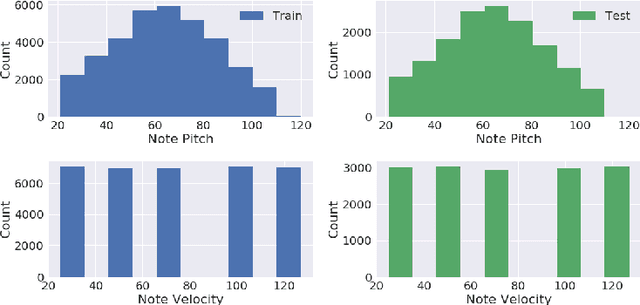
Audio signals are often represented as spectrograms and treated as 2D images. In this light, deep convolutional architectures are widely used for music audio tasks even though these two data types have very different structures. In this work, we attempt to "open the black-box" on deep convolutional models to inform future architectures for music audio tasks, and explain the excellent performance of deep convolutions that model spectrograms as 2D images. To this end, we expand recent explainability discussions in deep learning for natural image data to music audio data through systematic experiments using the deep features learned by various convolutional architectures. We demonstrate that deep convolutional features perform well across various target tasks, whether or not they are extracted from deep architectures originally trained on that task. Additionally, deep features exhibit high similarity to hand-crafted wavelet features, whether the deep features are extracted from a trained or untrained model.

An Interpretable Baseline for Time Series Classification Without Intensive Learning

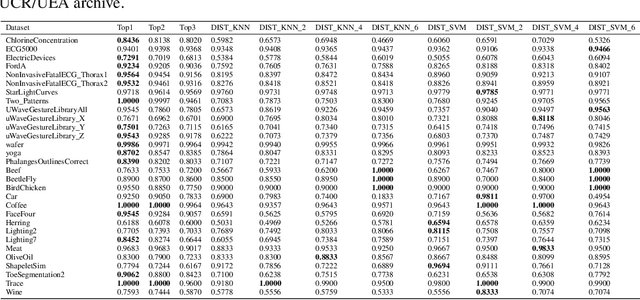
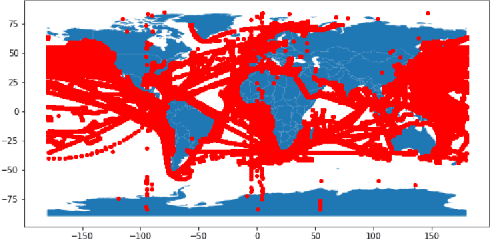
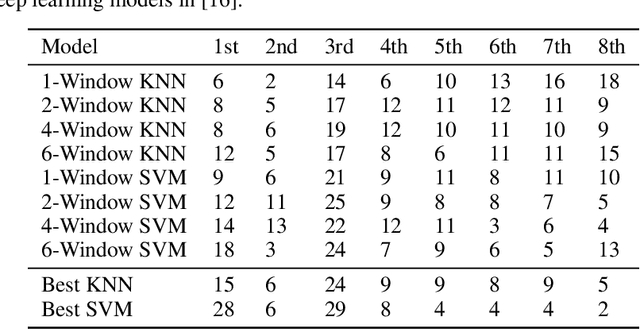
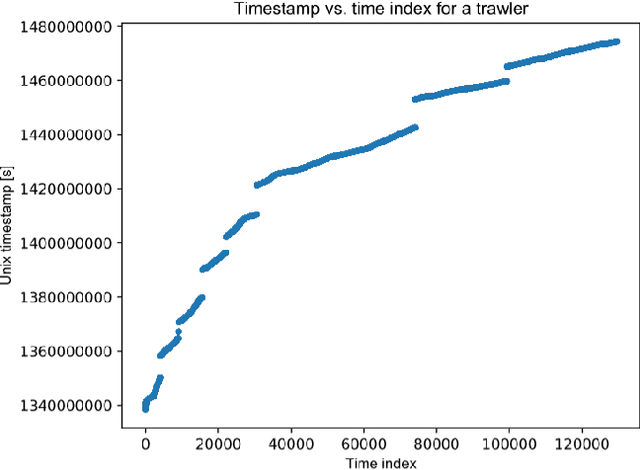
Recent advances in time series classification have largely focused on methods that either employ deep learning or utilize other machine learning models for feature extraction. Though such methods have proven powerful, they can also require computationally expensive models that may lack interpretability of results, or may require larger datasets than are freely available. In this paper, we propose an interpretable baseline based on representing each time series as a collection of probability distributions of extracted geometric features. The features used are intuitive and require minimal parameter tuning. We perform an exhaustive evaluation of our baseline on a large number of real datasets, showing that simple classifiers trained on these features exhibit surprising performance relative to state of the art methods requiring much more computational power. In particular, we show that our methodology achieves good performance on a challenging dataset involving the classification of fishing vessels, where our methods achieve good performance relative to the state of the art despite only having access to approximately two percent of the dataset used in training and evaluating this state of the art.

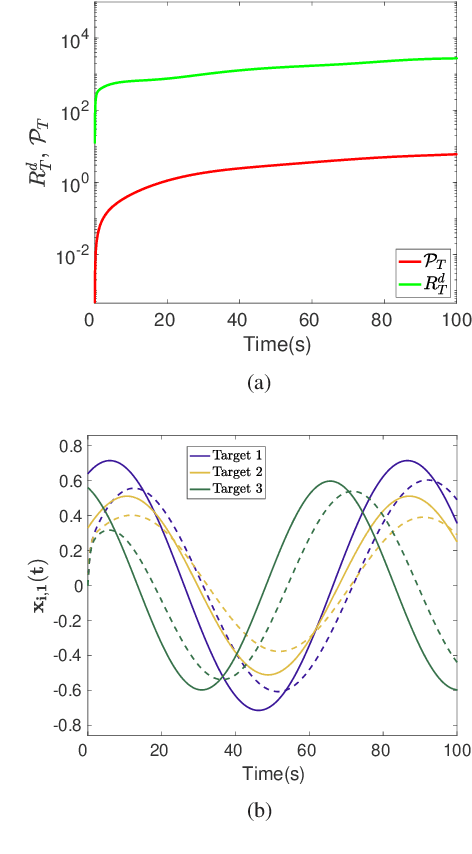
A Distributed Online Convex Optimization Algorithm with Improved Dynamic Regret

In this paper, we consider the problem of distributed online convex optimization, where a network of local agents aim to jointly optimize a convex function over a period of multiple time steps. The agents do not have any information about the future. Existing algorithms have established dynamic regret bounds that have explicit dependence on the number of time steps. In this work, we show that we can remove this dependence assuming that the local objective functions are strongly convex. More precisely, we propose a gradient tracking algorithm where agents jointly communicate and descend based on corrected gradient steps. We verify our theoretical results through numerical experiments.