Approximately Optimal Search on a Higher-dimensional Sliding Puzzle

Higher-dimensional sliding puzzles are constructed on the vertices of a $d$-dimensional hypercube, where $2^d-l$ vertices are distinctly coloured. Rings with the same colours are initially set randomly on the vertices of the hypercube. The goal of the puzzle is to move each of the $2^d-l$ rings to pre-defined target vertices on the cube. In this setting, the $k$-rule constraint represents a generalisation of edge collision for the movement of colours between vertices, allowing movement only when a hypercube face of dimension $k$ containing a ring is completely free of other rings. Starting from an initial configuration, what is the minimum number of moves needed to make ring colours match the vertex colours? An algorithm that provides us with such a number is called God's algorithm. When such an algorithm exists, it does not have a polynomial time complexity, at least in the case of the 15-puzzle corresponding to $k=1$ in the cubical puzzle. This paper presents a comprehensive computational study of different scenarios of the higher-dimensional puzzle. A benchmark of three computational techniques, an exact algorithm (the A* search) and two approximately optimal search techniques (an evolutionary algorithm (EA) and reinforcement learning (RL)) is presented in this work. The experiments show that all three methods can successfully solve the puzzle of dimension three for different face dimensions and across various difficulty levels. When the dimension increases, the A* search fails, and RL and EA methods can still provide a generally acceptable solution, i.e. a distribution of a number of moves with a median value of less than $30$. Overall, the EA method consistently requires less computational time, while failing in most cases to minimise the number of moves for the puzzle dimensions $d=4$ and $d=5$.

Meta-Posterior Consistency for the Bayesian Inference of Metastable System

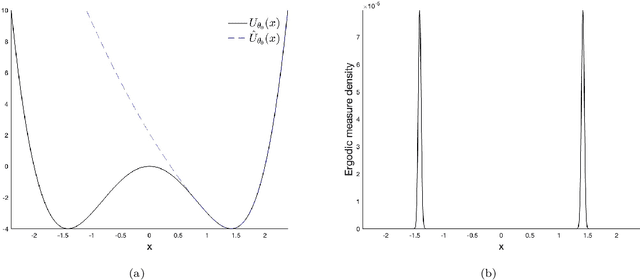
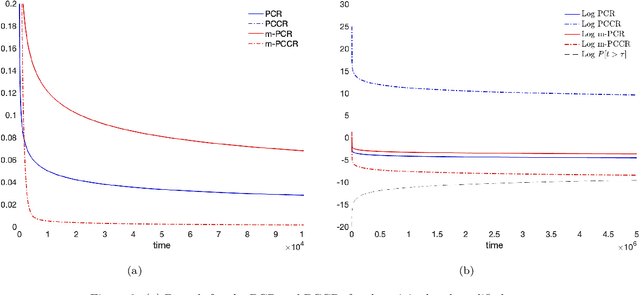
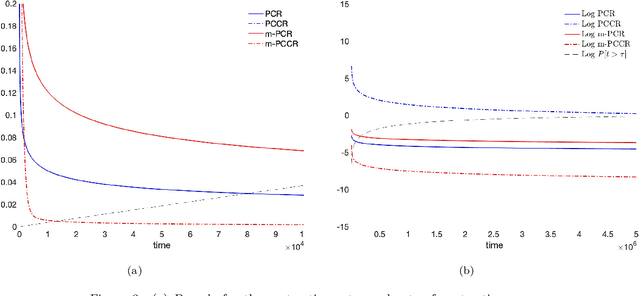
The vast majority of the literature on learning dynamical systems or stochastic processes from time series has focused on stable or ergodic systems, for both Bayesian and frequentist inference procedures. However, most real-world systems are only metastable, that is, the dynamics appear to be stable on some time scale, but are in fact unstable over longer time scales. Consistency of inference for metastable systems may not be possible, but one can ask about metaconsistency: Do inference procedures converge when observations are taken over a large but finite time interval, but diverge on longer time scales? In this paper we introduce, discuss, and quantify metaconsistency in a Bayesian framework. We discuss how metaconsistency can be exploited to efficiently infer a model for a sub-system of a larger system, where inference on the global behavior may require much more data. We also discuss the relation between meta-consistency and the spectral properties of the model dynamical system in the case of uniformly ergodic diffusions.

Pragmatist Intelligence: Where the Principle of Usefulness Can Take ANNs

Artificial neural networks (ANNs) perform extraordinarily on numerous tasks including classification or prediction, e.g., speech processing and image classification. These new functions are based on a computational model that is enabled to select freely all necessary internal model parameters as long as it eventually delivers the functionality it is supposed to exhibit. Here, we review the connection between the model parameter selection in machine learning (ML) algorithms running on ANNs and the epistemological theory of neopragmatism focusing on the theory's utility and anti-representationalist aspects. To understand the consequences of the model parameter selection of an ANN, we suggest using neopragmatist theories whose implications are well studied. Incidentally, neopragmatism's notion of optimization is also based on utility considerations. This means that applying this approach elegantly reveals the inherent connections between optimization in ML, using a numerical method during the learning phase, and optimization in the ethical theory of consequentialism, where it occurs as a maxim of action. We suggest that these connections originate from the way relevance is calculated in ML systems. This could ultimately reveal a tendency for specific actions in ML systems.

Scalable Bayesian inference for the generalized linear mixed model

The generalized linear mixed model (GLMM) is a popular statistical approach for handling correlated data, and is used extensively in applications areas where big data is common, including biomedical data settings. The focus of this paper is scalable statistical inference for the GLMM, where we define statistical inference as: (i) estimation of population parameters, and (ii) evaluation of scientific hypotheses in the presence of uncertainty. Artificial intelligence (AI) learning algorithms excel at scalable statistical estimation, but rarely include uncertainty quantification. In contrast, Bayesian inference provides full statistical inference, since uncertainty quantification results automatically from the posterior distribution. Unfortunately, Bayesian inference algorithms, including Markov Chain Monte Carlo (MCMC), become computationally intractable in big data settings. In this paper, we introduce a statistical inference algorithm at the intersection of AI and Bayesian inference, that leverages the scalability of modern AI algorithms with guaranteed uncertainty quantification that accompanies Bayesian inference. Our algorithm is an extension of stochastic gradient MCMC with novel contributions that address the treatment of correlated data (i.e., intractable marginal likelihood) and proper posterior variance estimation. Through theoretical and empirical results we establish our algorithm's statistical inference properties, and apply the method in a large electronic health records database.

Asymptotics of Bayesian Uncertainty Estimation in Random Features Regression

In this paper we compare and contrast the behavior of the posterior predictive distribution to the risk of the maximum a posteriori estimator for the random features regression model in the overparameterized regime. We will focus on the variance of the posterior predictive distribution (Bayesian model average) and compare its asymptotics to that of the risk of the MAP estimator. In the regime where the model dimensions grow faster than any constant multiple of the number of samples, asymptotic agreement between these two quantities is governed by the phase transition in the signal-to-noise ratio. They also asymptotically agree with each other when the number of samples grow faster than any constant multiple of model dimensions. Numerical simulations illustrate finer distributional properties of the two quantities for finite dimensions. We conjecture they have Gaussian fluctuations and exhibit similar properties as found by previous authors in a Gaussian sequence model, which is of independent theoretical interest.

Global Optimality of Elman-type RNN in the Mean-Field Regime

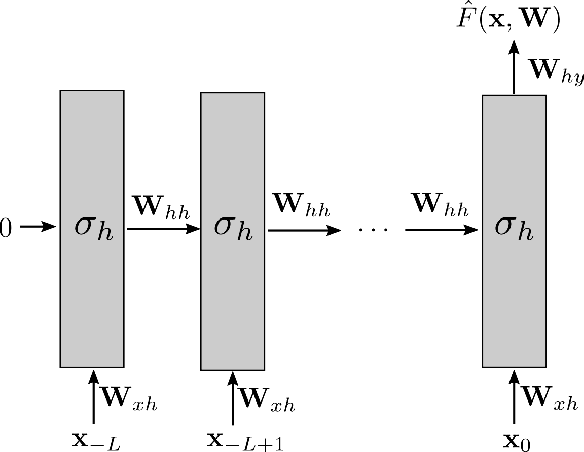
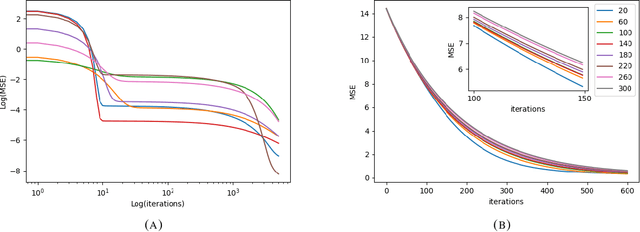
We analyze Elman-type Recurrent Reural Networks (RNNs) and their training in the mean-field regime. Specifically, we show convergence of gradient descent training dynamics of the RNN to the corresponding mean-field formulation in the large width limit. We also show that the fixed points of the limiting infinite-width dynamics are globally optimal, under some assumptions on the initialization of the weights. Our results establish optimality for feature-learning with wide RNNs in the mean-field regime

Concentration inequalities and optimal number of layers for stochastic deep neural networks

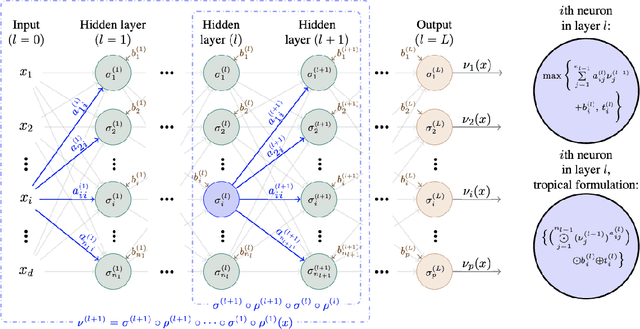
We state concentration and martingale inequalities for the output of the hidden layers of a stochastic deep neural network (SDNN), as well as for the output of the whole SDNN. These results allow us to introduce an expected classifier (EC), and to give probabilistic upper bound for the classification error of the EC. We also state the optimal number of layers for the SDNN via an optimal stopping procedure. We apply our analysis to a stochastic version of a feedforward neural network with ReLU activation function.

Learning Graph Partitions

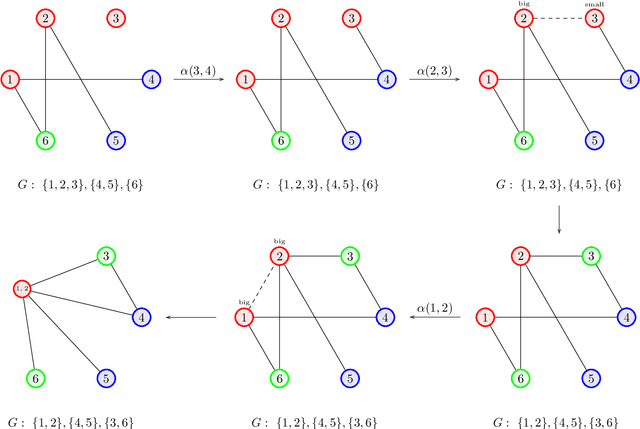
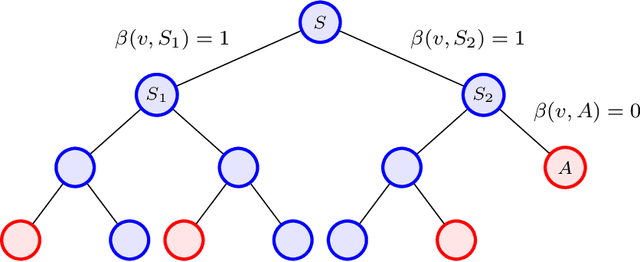
Given a partition of a graph into connected components, the membership oracle asserts whether any two vertices of the graph lie in the same component or not. We prove that for $n\ge k\ge 2$, learning the components of an $n$-vertex hidden graph with $k$ components requires at least $\frac{1}{2}(n-k)(k-1)$ membership queries. This proves the optimality of the $O(nk)$ algorithm proposed by Reyzin and Srivastava (2007) for this problem, improving on the best known information-theoretic bound of $\Omega(n\log k)$ queries. Further, we construct an oracle that can learn the number of components of $G$ in asymptotically fewer queries than learning the full partition, thus answering another question posed by the same authors. Lastly, we introduce a more applicable version of this oracle, and prove asymptotically tight bounds of $\widetilde\Theta(m)$ queries for both learning and verifying an $m$-edge hidden graph $G$ using this oracle.

Accelerating Markov Random Field Inference with Uncertainty Quantification

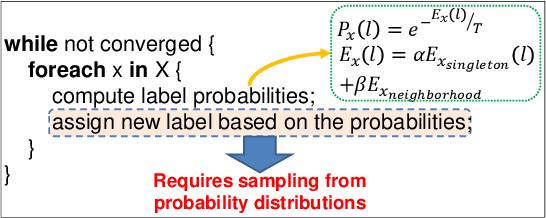
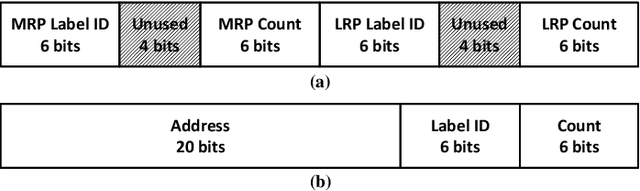
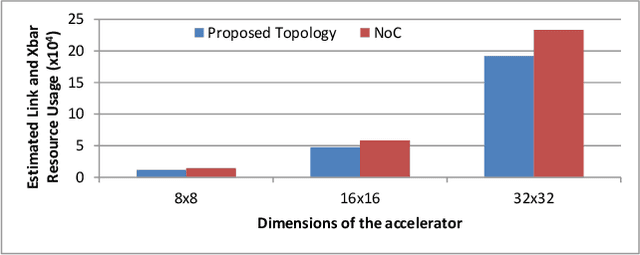
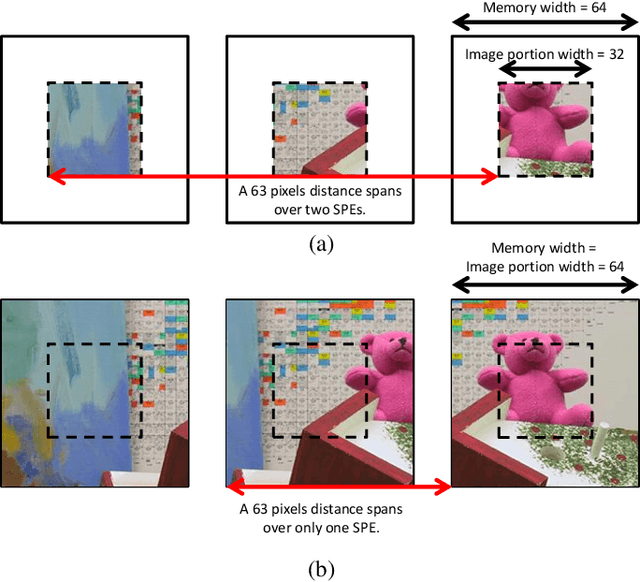
Statistical machine learning has widespread application in various domains. These methods include probabilistic algorithms, such as Markov Chain Monte-Carlo (MCMC), which rely on generating random numbers from probability distributions. These algorithms are computationally expensive on conventional processors, yet their statistical properties, namely interpretability and uncertainty quantification (UQ) compared to deep learning, make them an attractive alternative approach. Therefore, hardware specialization can be adopted to address the shortcomings of conventional processors in running these applications. In this paper, we propose a high-throughput accelerator for Markov Random Field (MRF) inference, a powerful model for representing a wide range of applications, using MCMC with Gibbs sampling. We propose a tiled architecture which takes advantage of near-memory computing, and memory optimizations tailored to the semantics of MRF. Additionally, we propose a novel hybrid on-chip/off-chip memory system and logging scheme to efficiently support UQ. This memory system design is not specific to MRF models and is applicable to applications using probabilistic algorithms. In addition, it dramatically reduces off-chip memory bandwidth requirements. We implemented an FPGA prototype of our proposed architecture using high-level synthesis tools and achieved 146MHz frequency for an accelerator with 32 function units on an Intel Arria 10 FPGA. Compared to prior work on FPGA, our accelerator achieves 26X speedup. Furthermore, our proposed memory system and logging scheme to support UQ reduces off-chip bandwidth by 71% for two applications. ASIC analysis in 15nm shows our design with 2048 function units running at 3GHz outperforms GPU implementations of motion estimation and stereo vision on Nvidia RTX2080Ti by 120X-210X, occupying only 7.7% of the area.

Towards Explainable Convolutional Features for Music Audio Modeling

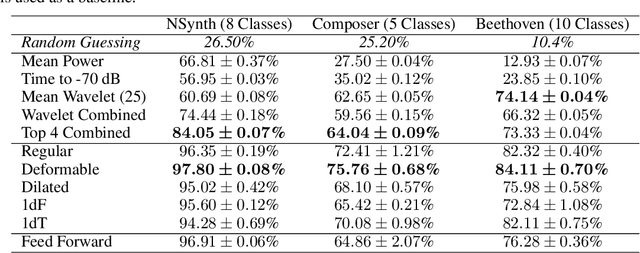
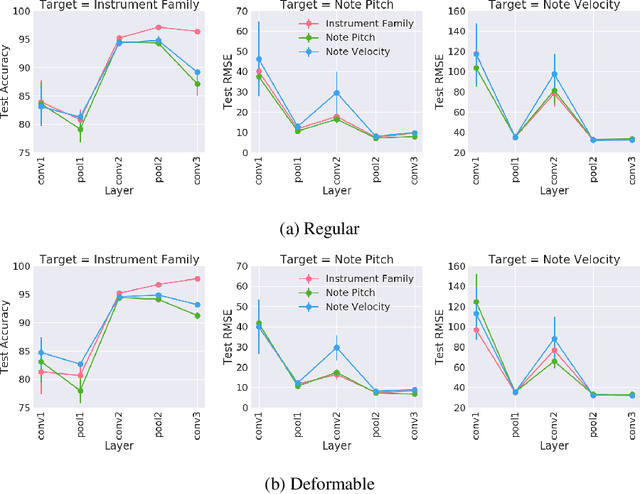
Audio signals are often represented as spectrograms and treated as 2D images. In this light, deep convolutional architectures are widely used for music audio tasks even though these two data types have very different structures. In this work, we attempt to "open the black-box" on deep convolutional models to inform future architectures for music audio tasks, and explain the excellent performance of deep convolutions that model spectrograms as 2D images. To this end, we expand recent explainability discussions in deep learning for natural image data to music audio data through systematic experiments using the deep features learned by various convolutional architectures. We demonstrate that deep convolutional features perform well across various target tasks, whether or not they are extracted from deep architectures originally trained on that task. Additionally, deep features exhibit high similarity to hand-crafted wavelet features, whether the deep features are extracted from a trained or untrained model.