Scalable Bayesian inference for the generalized linear mixed model

The generalized linear mixed model (GLMM) is a popular statistical approach for handling correlated data, and is used extensively in applications areas where big data is common, including biomedical data settings. The focus of this paper is scalable statistical inference for the GLMM, where we define statistical inference as: (i) estimation of population parameters, and (ii) evaluation of scientific hypotheses in the presence of uncertainty. Artificial intelligence (AI) learning algorithms excel at scalable statistical estimation, but rarely include uncertainty quantification. In contrast, Bayesian inference provides full statistical inference, since uncertainty quantification results automatically from the posterior distribution. Unfortunately, Bayesian inference algorithms, including Markov Chain Monte Carlo (MCMC), become computationally intractable in big data settings. In this paper, we introduce a statistical inference algorithm at the intersection of AI and Bayesian inference, that leverages the scalability of modern AI algorithms with guaranteed uncertainty quantification that accompanies Bayesian inference. Our algorithm is an extension of stochastic gradient MCMC with novel contributions that address the treatment of correlated data (i.e., intractable marginal likelihood) and proper posterior variance estimation. Through theoretical and empirical results we establish our algorithm's statistical inference properties, and apply the method in a large electronic health records database.

Asymptotics of Bayesian Uncertainty Estimation in Random Features Regression

In this paper we compare and contrast the behavior of the posterior predictive distribution to the risk of the maximum a posteriori estimator for the random features regression model in the overparameterized regime. We will focus on the variance of the posterior predictive distribution (Bayesian model average) and compare its asymptotics to that of the risk of the MAP estimator. In the regime where the model dimensions grow faster than any constant multiple of the number of samples, asymptotic agreement between these two quantities is governed by the phase transition in the signal-to-noise ratio. They also asymptotically agree with each other when the number of samples grow faster than any constant multiple of model dimensions. Numerical simulations illustrate finer distributional properties of the two quantities for finite dimensions. We conjecture they have Gaussian fluctuations and exhibit similar properties as found by previous authors in a Gaussian sequence model, which is of independent theoretical interest.

Scalable Modeling of Spatiotemporal Data using the Variational Autoencoder: an Application in Glaucoma

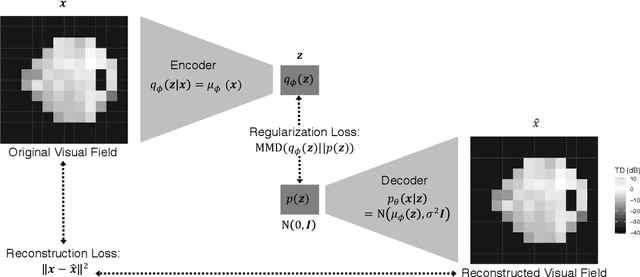
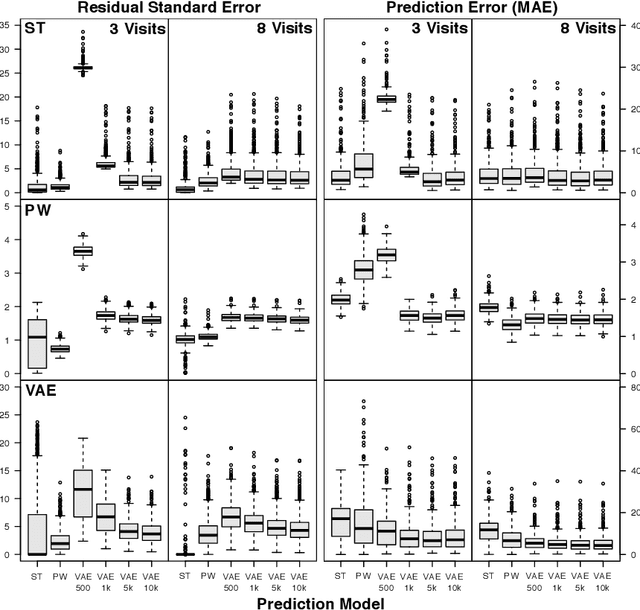
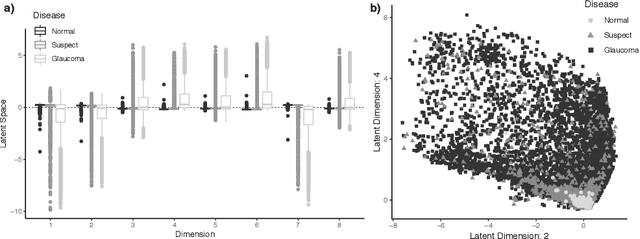
As big spatial data becomes increasingly prevalent, classical spatiotemporal (ST) methods often do not scale well. While methods have been developed to account for high-dimensional spatial objects, the setting where there are exceedingly large samples of spatial observations has had less attention. The variational autoencoder (VAE), an unsupervised generative model based on deep learning and approximate Bayesian inference, fills this void using a latent variable specification that is inferred jointly across the large number of samples. In this manuscript, we compare the performance of the VAE with a more classical ST method when analyzing longitudinal visual fields from a large cohort of patients in a prospective glaucoma study. Through simulation and a case study, we demonstrate that the VAE is a scalable method for analyzing ST data, when the goal is to obtain accurate predictions. R code to implement the VAE can be found on GitHub: https://github.com/berchuck/vaeST.