Emergence of meta-stable clustering in mean-field transformer models

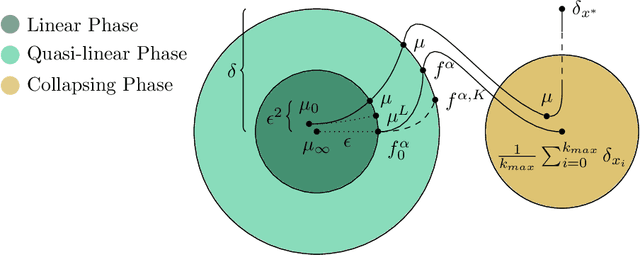
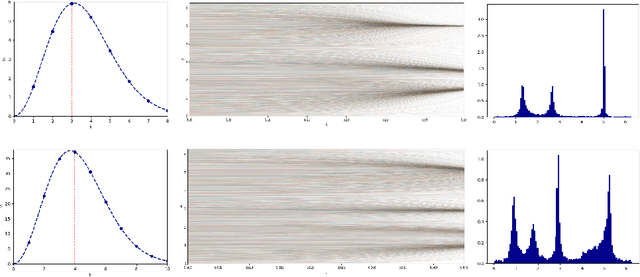
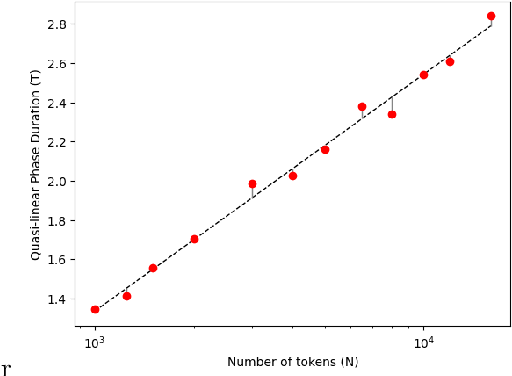
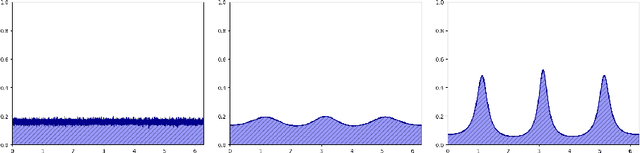
We model the evolution of tokens within a deep stack of Transformer layers as a continuous-time flow on the unit sphere, governed by a mean-field interacting particle system, building on the framework introduced in (Geshkovski et al., 2023). Studying the corresponding mean-field Partial Differential Equation (PDE), which can be interpreted as a Wasserstein gradient flow, in this paper we provide a mathematical investigation of the long-term behavior of this system, with a particular focus on the emergence and persistence of meta-stable phases and clustering phenomena, key elements in applications like next-token prediction. More specifically, we perform a perturbative analysis of the mean-field PDE around the iid uniform initialization and prove that, in the limit of large number of tokens, the model remains close to a meta-stable manifold of solutions with a given structure (e.g., periodicity). Further, the structure characterizing the meta-stable manifold is explicitly identified, as a function of the inverse temperature parameter of the model, by the index maximizing a certain rescaling of Gegenbauer polynomials.

Scalable Bayesian inference for the generalized linear mixed model

The generalized linear mixed model (GLMM) is a popular statistical approach for handling correlated data, and is used extensively in applications areas where big data is common, including biomedical data settings. The focus of this paper is scalable statistical inference for the GLMM, where we define statistical inference as: (i) estimation of population parameters, and (ii) evaluation of scientific hypotheses in the presence of uncertainty. Artificial intelligence (AI) learning algorithms excel at scalable statistical estimation, but rarely include uncertainty quantification. In contrast, Bayesian inference provides full statistical inference, since uncertainty quantification results automatically from the posterior distribution. Unfortunately, Bayesian inference algorithms, including Markov Chain Monte Carlo (MCMC), become computationally intractable in big data settings. In this paper, we introduce a statistical inference algorithm at the intersection of AI and Bayesian inference, that leverages the scalability of modern AI algorithms with guaranteed uncertainty quantification that accompanies Bayesian inference. Our algorithm is an extension of stochastic gradient MCMC with novel contributions that address the treatment of correlated data (i.e., intractable marginal likelihood) and proper posterior variance estimation. Through theoretical and empirical results we establish our algorithm's statistical inference properties, and apply the method in a large electronic health records database.

Global Optimality of Elman-type RNN in the Mean-Field Regime

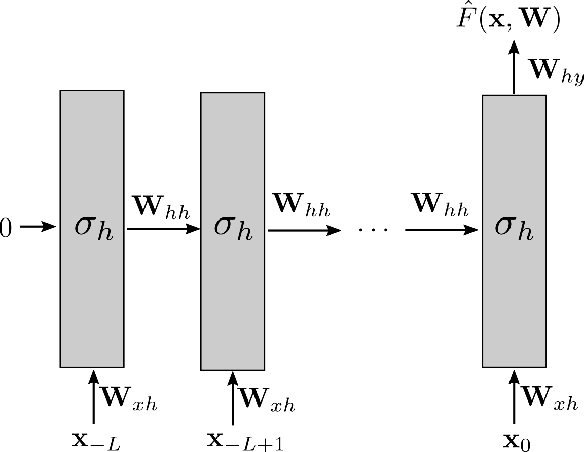
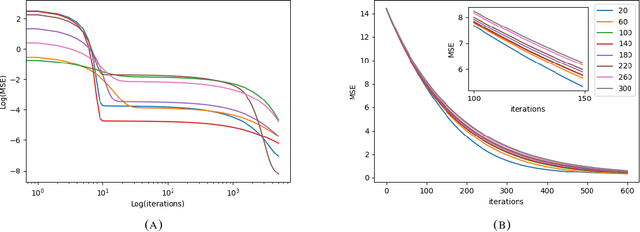
We analyze Elman-type Recurrent Reural Networks (RNNs) and their training in the mean-field regime. Specifically, we show convergence of gradient descent training dynamics of the RNN to the corresponding mean-field formulation in the large width limit. We also show that the fixed points of the limiting infinite-width dynamics are globally optimal, under some assumptions on the initialization of the weights. Our results establish optimality for feature-learning with wide RNNs in the mean-field regime

Global optimality of softmax policy gradient with single hidden layer neural networks in the mean-field regime

We study the problem of policy optimization for infinite-horizon discounted Markov Decision Processes with softmax policy and nonlinear function approximation trained with policy gradient algorithms. We concentrate on the training dynamics in the mean-field regime, modeling e.g., the behavior of wide single hidden layer neural networks, when exploration is encouraged through entropy regularization. The dynamics of these models is established as a Wasserstein gradient flow of distributions in parameter space. We further prove global optimality of the fixed points of this dynamics under mild conditions on their initialization.

Temporal-difference learning for nonlinear value function approximation in the lazy training regime

We discuss the approximation of the value function for infinite-horizon discounted Markov Decision Processes (MDP) with nonlinear functions trained with Temporal-Difference (TD) learning algorithm. We consider this problem under a certain scaling of the approximating function, leading to a regime called lazy training. In this regime the parameters of the model vary only slightly during the learning process, a feature that has recently been observed in the training of neural networks, where the scaling we study arises naturally, implicit in the initialization of their parameters. Both in the under- and over-parametrized frameworks, we prove exponential convergence to local, respectively global minimizers of the above algorithm in the lazy training regime. We then give examples of such convergence results in the case of models that diverge if trained with non-lazy TD learning, and in the case of neural networks.

Diffusion Fingerprints

We introduce, test and discuss a method for classifying and clustering data modeled as directed graphs. The idea is to start diffusion processes from any subset of a data collection, generating corresponding distributions for reaching points in the network. These distributions take the form of high-dimensional numerical vectors and capture essential topological properties of the original dataset. We show how these diffusion vectors can be successfully applied for getting state-of-the-art accuracies in the problem of extracting pathways from metabolic networks. We also provide a guideline to illustrate how to use our method for classification problems, and discuss important details of its implementation. In particular, we present a simple dimensionality reduction technique that lowers the computational cost of classifying diffusion vectors, while leaving the predictive power of the classification process substantially unaltered. Although the method has very few parameters, the results we obtain show its flexibility and power. This should make it helpful in many other contexts.