Diffusion Fingerprints

We introduce, test and discuss a method for classifying and clustering data modeled as directed graphs. The idea is to start diffusion processes from any subset of a data collection, generating corresponding distributions for reaching points in the network. These distributions take the form of high-dimensional numerical vectors and capture essential topological properties of the original dataset. We show how these diffusion vectors can be successfully applied for getting state-of-the-art accuracies in the problem of extracting pathways from metabolic networks. We also provide a guideline to illustrate how to use our method for classification problems, and discuss important details of its implementation. In particular, we present a simple dimensionality reduction technique that lowers the computational cost of classifying diffusion vectors, while leaving the predictive power of the classification process substantially unaltered. Although the method has very few parameters, the results we obtain show its flexibility and power. This should make it helpful in many other contexts.

Self reference in word definitions

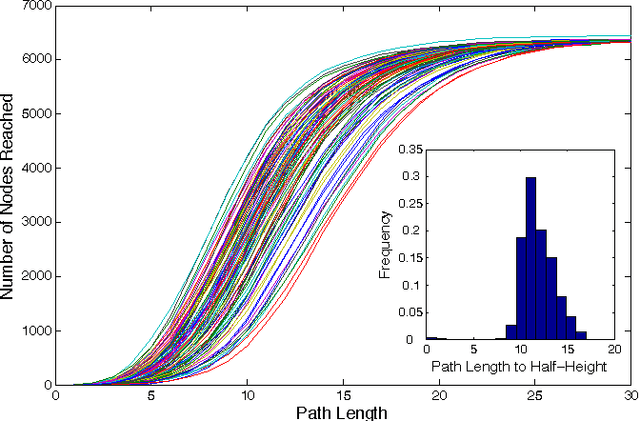
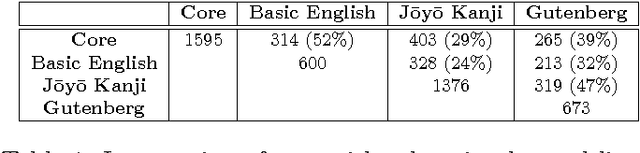
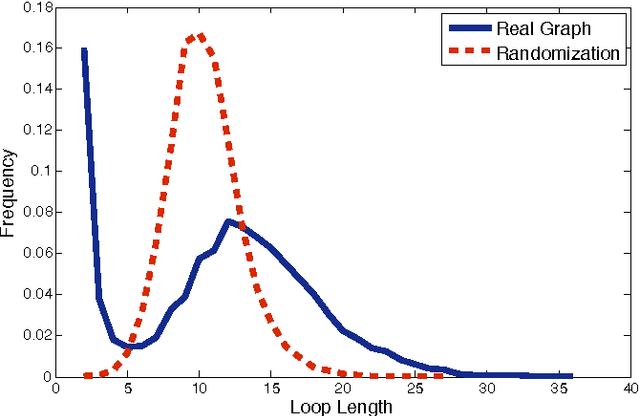
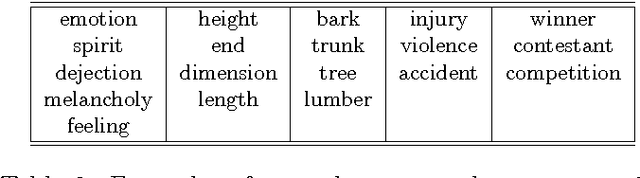
Dictionaries are inherently circular in nature. A given word is linked to a set of alternative words (the definition) which in turn point to further descendants. Iterating through definitions in this way, one typically finds that definitions loop back upon themselves. The graph formed by such definitional relations is our object of study. By eliminating those links which are not in loops, we arrive at a core subgraph of highly connected nodes. We observe that definitional loops are conveniently classified by length, with longer loops usually emerging from semantic misinterpretation. By breaking the long loops in the graph of the dictionary, we arrive at a set of disconnected clusters. We find that the words in these clusters constitute semantic units, and moreover tend to have been introduced into the English language at similar times, suggesting a possible mechanism for language evolution.