Emergence of meta-stable clustering in mean-field transformer models

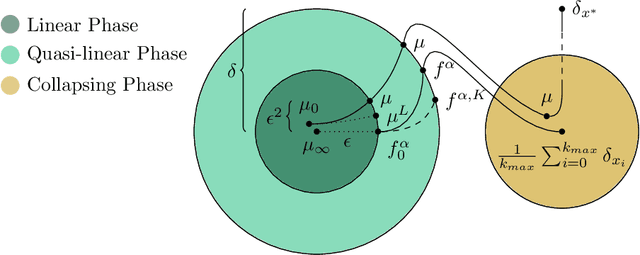
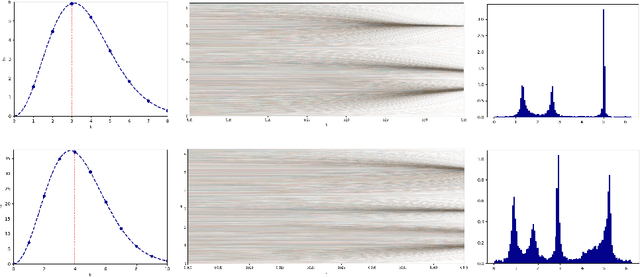
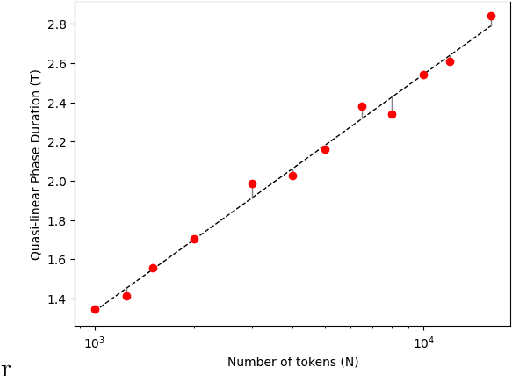
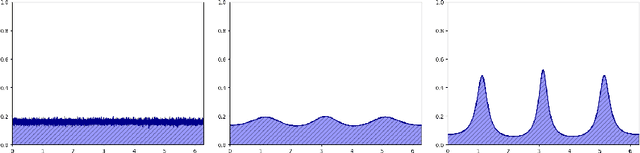
We model the evolution of tokens within a deep stack of Transformer layers as a continuous-time flow on the unit sphere, governed by a mean-field interacting particle system, building on the framework introduced in (Geshkovski et al., 2023). Studying the corresponding mean-field Partial Differential Equation (PDE), which can be interpreted as a Wasserstein gradient flow, in this paper we provide a mathematical investigation of the long-term behavior of this system, with a particular focus on the emergence and persistence of meta-stable phases and clustering phenomena, key elements in applications like next-token prediction. More specifically, we perform a perturbative analysis of the mean-field PDE around the iid uniform initialization and prove that, in the limit of large number of tokens, the model remains close to a meta-stable manifold of solutions with a given structure (e.g., periodicity). Further, the structure characterizing the meta-stable manifold is explicitly identified, as a function of the inverse temperature parameter of the model, by the index maximizing a certain rescaling of Gegenbauer polynomials.

The Challenges of the Nonlinear Regime for Physics-Informed Neural Networks

The Neural Tangent Kernel (NTK) viewpoint represents a valuable approach to examine the training dynamics of Physics-Informed Neural Networks (PINNs) in the infinite width limit. We leverage this perspective and focus on the case of nonlinear Partial Differential Equations (PDEs) solved by PINNs. We provide theoretical results on the different behaviors of the NTK depending on the linearity of the differential operator. Moreover, inspired by our theoretical results, we emphasize the advantage of employing second-order methods for training PINNs. Additionally, we explore the convergence capabilities of second-order methods and address the challenges of spectral bias and slow convergence. Every theoretical result is supported by numerical examples with both linear and nonlinear PDEs, and we validate our training method on benchmark test cases.