Phantora: Live GPU Cluster Simulation for Machine Learning System Performance Estimation

To accommodate ever-increasing model complexity, modern machine learning (ML) systems have to scale to large GPU clusters. Changes in ML model architecture, ML system implementation, and cluster configuration can significantly affect overall ML system performance. However, quantifying the performance impact before deployment is challenging. Existing performance estimation methods use performance modeling or static workload simulation. These techniques are not general: they requires significant human effort and computation capacity to generate training data or a workload. It is also difficult to adapt ML systems to use these techniques. This paper introduces, Phantora, a live GPU cluster simulator for performance estimation. Phantora runs minimally modified ML models and frameworks, intercepting and simulating GPU-related operations to enable high-fidelity performance estimation. Phantora overcomes several research challenges in integrating an event-driven network simulator with live system execution, and introduces a set of techniques to improve simulation speed, scalability, and accuracy. Our evaluation results show that Phantora can deliver similar estimation accuracy to the state-of-the-art workload simulation approach with only one GPU, while reducing human effort and increasing generalizability.

Accelerating Markov Random Field Inference with Uncertainty Quantification

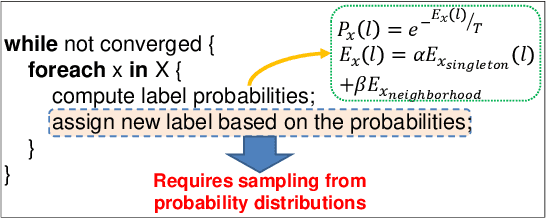
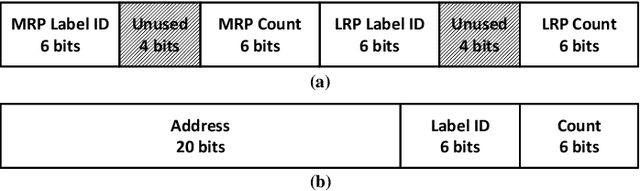
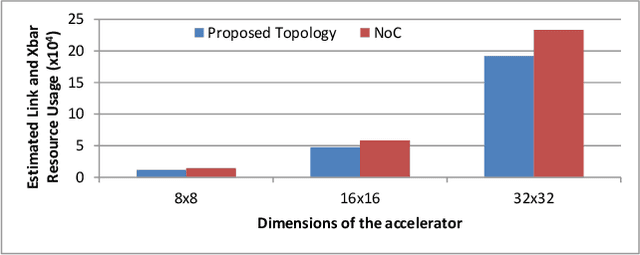
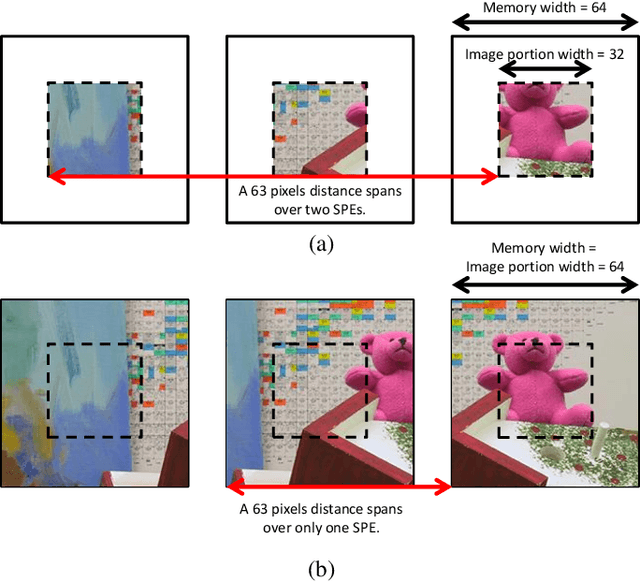
Statistical machine learning has widespread application in various domains. These methods include probabilistic algorithms, such as Markov Chain Monte-Carlo (MCMC), which rely on generating random numbers from probability distributions. These algorithms are computationally expensive on conventional processors, yet their statistical properties, namely interpretability and uncertainty quantification (UQ) compared to deep learning, make them an attractive alternative approach. Therefore, hardware specialization can be adopted to address the shortcomings of conventional processors in running these applications. In this paper, we propose a high-throughput accelerator for Markov Random Field (MRF) inference, a powerful model for representing a wide range of applications, using MCMC with Gibbs sampling. We propose a tiled architecture which takes advantage of near-memory computing, and memory optimizations tailored to the semantics of MRF. Additionally, we propose a novel hybrid on-chip/off-chip memory system and logging scheme to efficiently support UQ. This memory system design is not specific to MRF models and is applicable to applications using probabilistic algorithms. In addition, it dramatically reduces off-chip memory bandwidth requirements. We implemented an FPGA prototype of our proposed architecture using high-level synthesis tools and achieved 146MHz frequency for an accelerator with 32 function units on an Intel Arria 10 FPGA. Compared to prior work on FPGA, our accelerator achieves 26X speedup. Furthermore, our proposed memory system and logging scheme to support UQ reduces off-chip bandwidth by 71% for two applications. ASIC analysis in 15nm shows our design with 2048 function units running at 3GHz outperforms GPU implementations of motion estimation and stereo vision on Nvidia RTX2080Ti by 120X-210X, occupying only 7.7% of the area.

Beyond Application End-Point Results: Quantifying Statistical Robustness of MCMC Accelerators

Statistical machine learning often uses probabilistic algorithms, such as Markov Chain Monte Carlo (MCMC), to solve a wide range of problems. Probabilistic computations, often considered too slow on conventional processors, can be accelerated with specialized hardware by exploiting parallelism and optimizing the design using various approximation techniques. Current methodologies for evaluating correctness of probabilistic accelerators are often incomplete, mostly focusing only on end-point result quality ("accuracy"). It is important for hardware designers and domain experts to look beyond end-point "accuracy" and be aware of the hardware optimizations impact on other statistical properties. This work takes a first step towards defining metrics and a methodology for quantitatively evaluating correctness of probabilistic accelerators beyond end-point result quality. We propose three pillars of statistical robustness: 1) sampling quality, 2) convergence diagnostic, and 3) goodness of fit. We apply our framework to a representative MCMC accelerator and surface design issues that cannot be exposed using only application end-point result quality. Applying the framework to guide design space exploration shows that statistical robustness comparable to floating-point software can be achieved by slightly increasing the bit representation, without floating-point hardware requirements.

A Case for Quantifying Statistical Robustness of Specialized Probabilistic AI Accelerators

Statistical machine learning often uses probabilistic algorithms, such as Markov Chain Monte Carlo (MCMC), to solve a wide range of problems. Many accelerators are proposed using specialized hardware to address sampling inefficiency, the critical performance bottleneck of probabilistic algorithms. These accelerators usually improve the hardware efficiency by using some approximation techniques, such as reducing bit representation, truncating small values to zero, or simplifying the Random Number Generator (RNG). Understanding the influence of these approximations on result quality is crucial to meeting the quality requirements of real applications. Although a common approach is to compare the end-point result quality using community-standard benchmarks and metrics, we claim a probabilistic architecture should provide some measure (or guarantee) of statistical robustness. This work takes a first step towards quantifying the statistical robustness of specialized hardware MCMC accelerators by proposing three pillars of statistical robustness: sampling quality, convergence diagnostic, and goodness of fit. Each pillar has at least one quantitative metric without the need to know the ground truth data. We apply this method to analyze the statistical robustness of an MCMC accelerator proposed by previous work, with some modifications, as a case study. The method also applies to other probabilistic accelerators and can be used in design space exploration.