Learning Graph Partitions
Paper and Code
Dec 15, 2021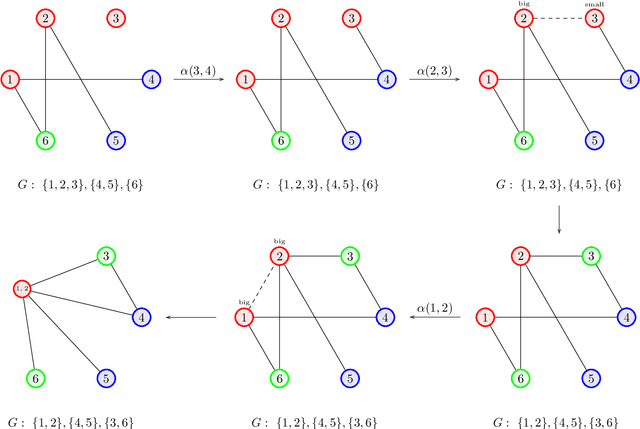
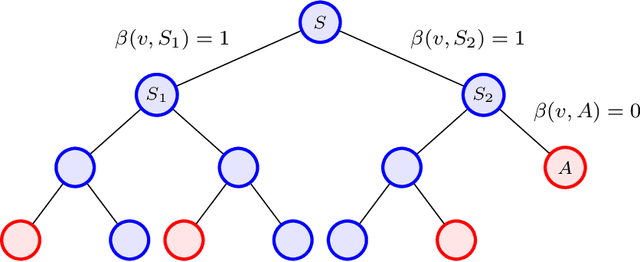
Given a partition of a graph into connected components, the membership oracle asserts whether any two vertices of the graph lie in the same component or not. We prove that for $n\ge k\ge 2$, learning the components of an $n$-vertex hidden graph with $k$ components requires at least $\frac{1}{2}(n-k)(k-1)$ membership queries. This proves the optimality of the $O(nk)$ algorithm proposed by Reyzin and Srivastava (2007) for this problem, improving on the best known information-theoretic bound of $\Omega(n\log k)$ queries. Further, we construct an oracle that can learn the number of components of $G$ in asymptotically fewer queries than learning the full partition, thus answering another question posed by the same authors. Lastly, we introduce a more applicable version of this oracle, and prove asymptotically tight bounds of $\widetilde\Theta(m)$ queries for both learning and verifying an $m$-edge hidden graph $G$ using this oracle.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge