PrACTiS: Perceiver-Attentional Copulas for Time Series

Transformers incorporating copula structures have demonstrated remarkable performance in time series prediction. However, their heavy reliance on self-attention mechanisms demands substantial computational resources, thus limiting their practical utility across a wide range of tasks. In this work, we present a model that combines the perceiver architecture with a copula structure to enhance time-series forecasting. By leveraging the perceiver as the encoder, we efficiently transform complex, high-dimensional, multimodal data into a compact latent space, thereby significantly reducing computational demands. To further reduce complexity, we introduce midpoint inference and local attention mechanisms, enabling the model to capture dependencies within imputed samples effectively. Subsequently, we deploy the copula-based attention and output variance testing mechanism to capture the joint distribution of missing data, while simultaneously mitigating error propagation during prediction. Our experimental results on the unimodal and multimodal benchmarks showcase a consistent 20\% improvement over the state-of-the-art methods, while utilizing less than half of available memory resources.

Semi-Empirical Objective Functions for MCMC Proposal Optimization

We introduce and demonstrate a semi-empirical procedure for determining approximate objective functions suitable for optimizing arbitrarily parameterized proposal distributions in MCMC methods. Our proposed Ab Initio objective functions consist of the weighted combination of functions following constraints on their global optima and of coordinate invariance that we argue should be upheld by general measures of MCMC efficiency for use in proposal optimization. The coefficients of Ab Initio objective functions are determined so as to recover the optimal MCMC behavior prescribed by established theoretical analysis for chosen reference problems. Our experimental results demonstrate that Ab Initio objective functions maintain favorable performance and preferable optimization behavior compared to existing objective functions for MCMC optimization when optimizing highly expressive proposal distributions. We argue that Ab Initio objective functions are sufficiently robust to enable the confident optimization of MCMC proposal distributions parameterized by deep generative networks that extend beyond the traditional limitations of individual MCMC schemes.

Projected Latent Markov Chain Monte Carlo: Conditional Inference with Normalizing Flows

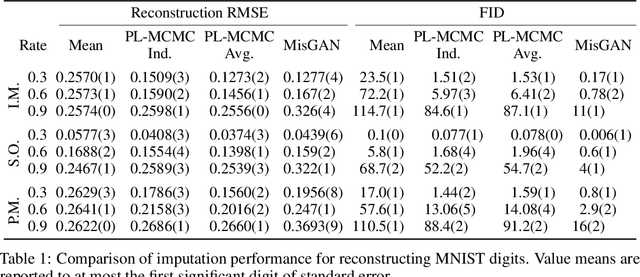
We introduce Projected Latent Markov Chain Monte Carlo (PL-MCMC), a technique for sampling from the high-dimensional conditional distributions learned by a normalizing flow. We prove that PL-MCMC asymptotically samples from the exact conditional distributions associated with a normalizing flow. As a conditional sampling method, PL-MCMC enables Monte Carlo Expectation Maximization (MC-EM) training of normalizing flows from incomplete data. By providing experimental results for a variety of data sets, we demonstrate the practicality and effectiveness of PL-MCMC for missing data inference using normalizing flows.

Perception-Distortion Trade-off with Restricted Boltzmann Machines

In this work, we introduce a new procedure for applying Restricted Boltzmann Machines (RBMs) to missing data inference tasks, based on linearization of the effective energy function governing the distribution of observations. We compare the performance of our proposed procedure with those obtained using existing reconstruction procedures trained on incomplete data. We place these performance comparisons within the context of the perception-distortion trade-off observed in other data reconstruction tasks, which has, until now, remained unexplored in tasks relying on incomplete training data.