Ali Hasan
Score-based Metropolis-Hastings for Fractional Langevin Algorithms
Jan 31, 2026Abstract:Sampling from heavy-tailed and multimodal distributions is challenging when neither the target density nor the proposal density can be evaluated, as in $α$-stable Lévy-driven fractional Langevin algorithms. While the target distribution can be estimated from data via score-based or energy-based models, the $α$-stable proposal density and its score are generally unavailable, rendering classical density-based Metropolis--Hastings (MH) corrections impractical. Consequently, existing fractional Langevin methods operate in an unadjusted regime and can exhibit substantial finite-time errors and poor empirical control of tail behavior. We introduce the Metropolis-Adjusted Fractional Langevin Algorithm (MAFLA), an MH-inspired, fully score-based correction mechanism. MAFLA employs designed proxies for fractional proposal score gradients under isotropic symmetric $α$-stable noise and learns an acceptance function via Score Balance Matching. We empirically illustrate the strong performance of MAFLA on a series of tasks including combinatorial optimization problems where the method significantly improves finite time sampling accuracy over unadjusted fractional Langevin dynamics.
Conditional Average Treatment Effect Estimation Under Hidden Confounders
Jun 14, 2025Abstract:One of the major challenges in estimating conditional potential outcomes and conditional average treatment effects (CATE) is the presence of hidden confounders. Since testing for hidden confounders cannot be accomplished only with observational data, conditional unconfoundedness is commonly assumed in the literature of CATE estimation. Nevertheless, under this assumption, CATE estimation can be significantly biased due to the effects of unobserved confounders. In this work, we consider the case where in addition to a potentially large observational dataset, a small dataset from a randomized controlled trial (RCT) is available. Notably, we make no assumptions on the existence of any covariate information for the RCT dataset, we only require the outcomes to be observed. We propose a CATE estimation method based on a pseudo-confounder generator and a CATE model that aligns the learned potential outcomes from the observational data with those observed from the RCT. Our method is applicable to many practical scenarios of interest, particularly those where privacy is a concern (e.g., medical applications). Extensive numerical experiments are provided demonstrating the effectiveness of our approach for both synthetic and real-world datasets.
Elliptic Loss Regularization
Mar 04, 2025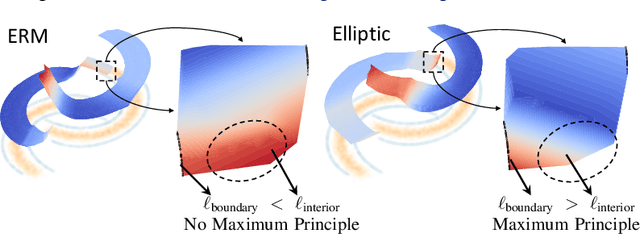

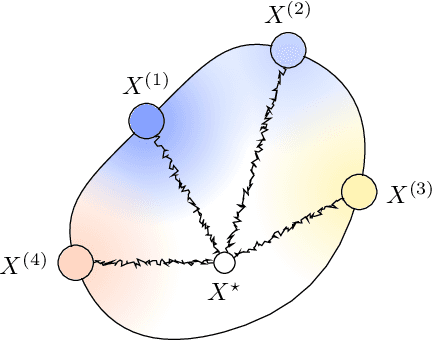
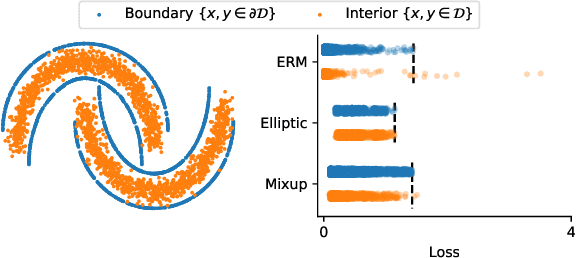
Abstract:Regularizing neural networks is important for anticipating model behavior in regions of the data space that are not well represented. In this work, we propose a regularization technique for enforcing a level of smoothness in the mapping between the data input space and the loss value. We specify the level of regularity by requiring that the loss of the network satisfies an elliptic operator over the data domain. To do this, we modify the usual empirical risk minimization objective such that we instead minimize a new objective that satisfies an elliptic operator over points within the domain. This allows us to use existing theory on elliptic operators to anticipate the behavior of the error for points outside the training set. We propose a tractable computational method that approximates the behavior of the elliptic operator while being computationally efficient. Finally, we analyze the properties of the proposed regularization to understand the performance on common problems of distribution shift and group imbalance. Numerical experiments confirm the utility of the proposed regularization technique.
Parabolic Continual Learning
Mar 03, 2025



Abstract:Regularizing continual learning techniques is important for anticipating algorithmic behavior under new realizations of data. We introduce a new approach to continual learning by imposing the properties of a parabolic partial differential equation (PDE) to regularize the expected behavior of the loss over time. This class of parabolic PDEs has a number of favorable properties that allow us to analyze the error incurred through forgetting and the error induced through generalization. Specifically, we do this through imposing boundary conditions where the boundary is given by a memory buffer. By using the memory buffer as a boundary, we can enforce long term dependencies by bounding the expected error by the boundary loss. Finally, we illustrate the empirical performance of the method on a series of continual learning tasks.
Score-Based Metropolis-Hastings Algorithms
Dec 31, 2024



Abstract:In this paper, we introduce a new approach for integrating score-based models with the Metropolis-Hastings algorithm. While traditional score-based diffusion models excel in accurately learning the score function from data points, they lack an energy function, making the Metropolis-Hastings adjustment step inaccessible. Consequently, the unadjusted Langevin algorithm is often used for sampling using estimated score functions. The lack of an energy function then prevents the application of the Metropolis-adjusted Langevin algorithm and other Metropolis-Hastings methods, limiting the wealth of other algorithms developed that use acceptance functions. We address this limitation by introducing a new loss function based on the \emph{detailed balance condition}, allowing the estimation of the Metropolis-Hastings acceptance probabilities given a learned score function. We demonstrate the effectiveness of the proposed method for various scenarios, including sampling from heavy-tail distributions.
Distributionally Robust Optimization as a Scalable Framework to Characterize Extreme Value Distributions
Jul 31, 2024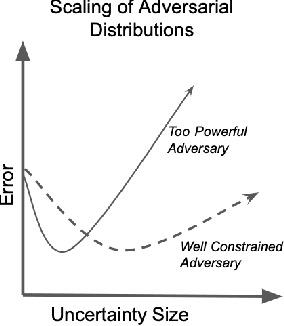


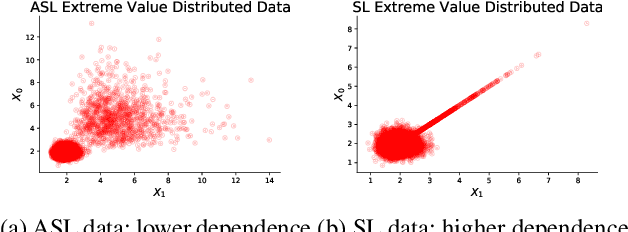
Abstract:The goal of this paper is to develop distributionally robust optimization (DRO) estimators, specifically for multidimensional Extreme Value Theory (EVT) statistics. EVT supports using semi-parametric models called max-stable distributions built from spatial Poisson point processes. While powerful, these models are only asymptotically valid for large samples. However, since extreme data is by definition scarce, the potential for model misspecification error is inherent to these applications, thus DRO estimators are natural. In order to mitigate over-conservative estimates while enhancing out-of-sample performance, we study DRO estimators informed by semi-parametric max-stable constraints in the space of point processes. We study both tractable convex formulations for some problems of interest (e.g. CVaR) and more general neural network based estimators. Both approaches are validated using synthetically generated data, recovering prescribed characteristics, and verifying the efficacy of the proposed techniques. Additionally, the proposed method is applied to a real data set of financial returns for comparison to a previous analysis. We established the proposed model as a novel formulation in the multivariate EVT domain, and innovative with respect to performance when compared to relevant alternate proposals.
Base Models for Parabolic Partial Differential Equations
Jul 17, 2024Abstract:Parabolic partial differential equations (PDEs) appear in many disciplines to model the evolution of various mathematical objects, such as probability flows, value functions in control theory, and derivative prices in finance. It is often necessary to compute the solutions or a function of the solutions to a parametric PDE in multiple scenarios corresponding to different parameters of this PDE. This process often requires resolving the PDEs from scratch, which is time-consuming. To better employ existing simulations for the PDEs, we propose a framework for finding solutions to parabolic PDEs across different scenarios by meta-learning an underlying base distribution. We build upon this base distribution to propose a method for computing solutions to parametric PDEs under different parameter settings. Finally, we illustrate the application of the proposed methods through extensive experiments in generative modeling, stochastic control, and finance. The empirical results suggest that the proposed approach improves generalization to solving PDEs under new parameter regimes.
Neural McKean-Vlasov Processes: Distributional Dependence in Diffusion Processes
Apr 15, 2024Abstract:McKean-Vlasov stochastic differential equations (MV-SDEs) provide a mathematical description of the behavior of an infinite number of interacting particles by imposing a dependence on the particle density. As such, we study the influence of explicitly including distributional information in the parameterization of the SDE. We propose a series of semi-parametric methods for representing MV-SDEs, and corresponding estimators for inferring parameters from data based on the properties of the MV-SDE. We analyze the characteristics of the different architectures and estimators, and consider their applicability in relevant machine learning problems. We empirically compare the performance of the different architectures and estimators on real and synthetic datasets for time series and probabilistic modeling. The results suggest that explicitly including distributional dependence in the parameterization of the SDE is effective in modeling temporal data with interaction under an exchangeability assumption while maintaining strong performance for standard It\^o-SDEs due to the richer class of probability flows associated with MV-SDEs.
PrACTiS: Perceiver-Attentional Copulas for Time Series
Oct 03, 2023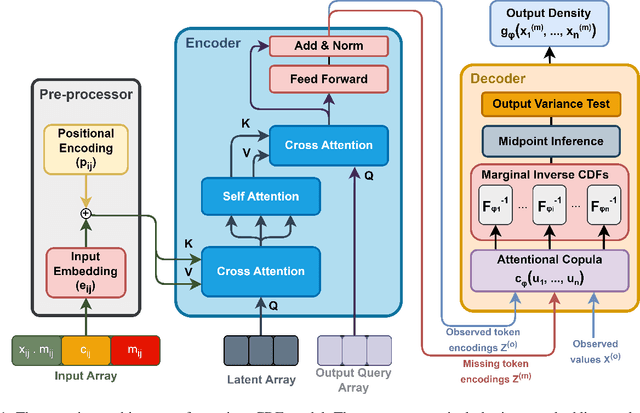
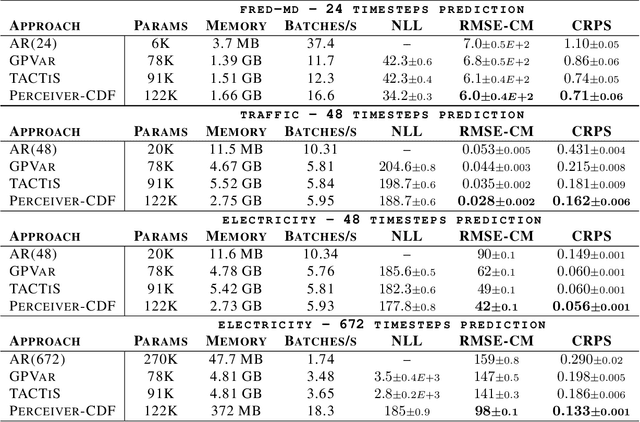
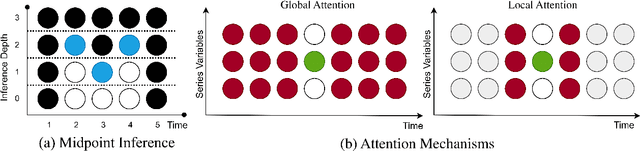
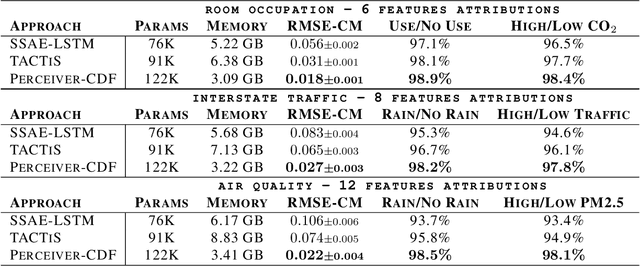
Abstract:Transformers incorporating copula structures have demonstrated remarkable performance in time series prediction. However, their heavy reliance on self-attention mechanisms demands substantial computational resources, thus limiting their practical utility across a wide range of tasks. In this work, we present a model that combines the perceiver architecture with a copula structure to enhance time-series forecasting. By leveraging the perceiver as the encoder, we efficiently transform complex, high-dimensional, multimodal data into a compact latent space, thereby significantly reducing computational demands. To further reduce complexity, we introduce midpoint inference and local attention mechanisms, enabling the model to capture dependencies within imputed samples effectively. Subsequently, we deploy the copula-based attention and output variance testing mechanism to capture the joint distribution of missing data, while simultaneously mitigating error propagation during prediction. Our experimental results on the unimodal and multimodal benchmarks showcase a consistent 20\% improvement over the state-of-the-art methods, while utilizing less than half of available memory resources.
Individual Treatment Effects in Extreme Regimes
Jun 20, 2023Abstract:Understanding individual treatment effects in extreme regimes is important for characterizing risks associated with different interventions. This is hindered by the fact that extreme regime data may be hard to collect, as it is scarcely observed in practice. In addressing this issue, we propose a new framework for estimating the individual treatment effect in extreme regimes (ITE$_2$). Specifically, we quantify this effect by the changes in the tail decay rates of potential outcomes in the presence or absence of the treatment. Subsequently, we establish conditions under which ITE$_2$ may be calculated and develop algorithms for its computation. We demonstrate the efficacy of our proposed method on various synthetic and semi-synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge