C-3DPO: Constrained Controlled Classification for Direct Preference Optimization

Direct preference optimization (DPO)-style algorithms have emerged as a promising approach for solving the alignment problem in AI. We present a novel perspective that formulates these algorithms as implicit classification algorithms. This classification framework enables us to recover many variants of DPO-style algorithms by choosing appropriate classification labels and loss functions. We then leverage this classification framework to demonstrate that the underlying problem solved in these algorithms is under-specified, making them susceptible to probability collapse of the winner-loser responses. We address this by proposing a set of constraints designed to control the movement of probability mass between the winner and loser in the reference and target policies. Our resulting algorithm, which we call Constrained Controlled Classification DPO (\texttt{C-3DPO}), has a meaningful RLHF interpretation. By hedging against probability collapse, \texttt{C-3DPO} provides practical improvements over vanilla \texttt{DPO} when aligning several large language models using standard preference datasets.

Adjoint sharding for very long context training of state space models

Despite very fast progress, efficiently training large language models (LLMs) in very long contexts remains challenging. Existing methods fall back to training LLMs with short contexts (a maximum of a few thousands tokens in training) and use inference time techniques when evaluating on long contexts (above 1M tokens context window at inference). As opposed to long-context-inference, training on very long context input prompts is quickly limited by GPU memory availability and by the prohibitively long training times it requires on state-of-the-art hardware. Meanwhile, many real-life applications require not only inference but also training/fine-tuning with long context on specific tasks. Such applications include, for example, augmenting the context with various sources of raw reference information for fact extraction, fact summarization, or fact reconciliation tasks. We propose adjoint sharding, a novel technique that comprises sharding gradient calculation during training to reduce memory requirements by orders of magnitude, making training on very long context computationally tractable. Adjoint sharding is based on the adjoint method and computes equivalent gradients to backpropagation. We also propose truncated adjoint sharding to speed up the algorithm while maintaining performance. We provide a distributed version, and a paralleled version of adjoint sharding to further speed up training. Empirical results show the proposed adjoint sharding algorithm reduces memory usage by up to 3X with a 1.27B parameter large language model on 1M context length training. This allows to increase the maximum context length during training or fine-tuning of a 1.27B parameter model from 35K tokens to above 100K tokens on a training infrastructure composed of five AWS P4 instances.

Base Models for Parabolic Partial Differential Equations

Parabolic partial differential equations (PDEs) appear in many disciplines to model the evolution of various mathematical objects, such as probability flows, value functions in control theory, and derivative prices in finance. It is often necessary to compute the solutions or a function of the solutions to a parametric PDE in multiple scenarios corresponding to different parameters of this PDE. This process often requires resolving the PDEs from scratch, which is time-consuming. To better employ existing simulations for the PDEs, we propose a framework for finding solutions to parabolic PDEs across different scenarios by meta-learning an underlying base distribution. We build upon this base distribution to propose a method for computing solutions to parametric PDEs under different parameter settings. Finally, we illustrate the application of the proposed methods through extensive experiments in generative modeling, stochastic control, and finance. The empirical results suggest that the proposed approach improves generalization to solving PDEs under new parameter regimes.

Characteristic Neural Ordinary Differential Equations

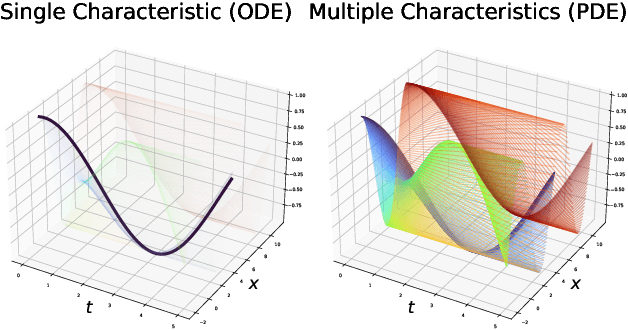
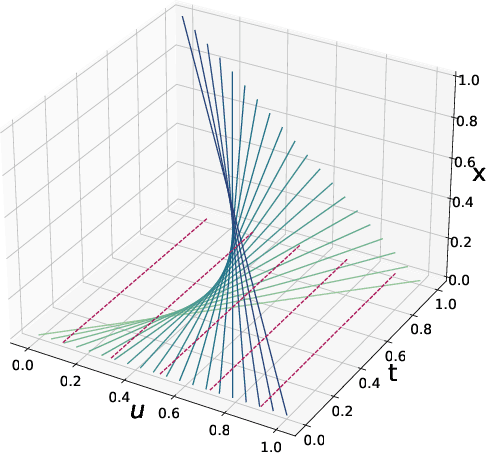
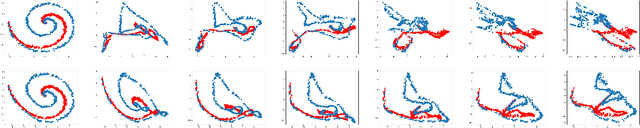
We propose Characteristic Neural Ordinary Differential Equations (C-NODEs), a framework for extending Neural Ordinary Differential Equations (NODEs) beyond ODEs. While NODEs model the evolution of the latent state as the solution to an ODE, the proposed C-NODE models the evolution of the latent state as the solution of a family of first-order quasi-linear partial differential equations (PDE) on their characteristics, defined as curves along which the PDEs reduce to ODEs. The reduction, in turn, allows the application of the standard frameworks for solving ODEs to PDE settings. Additionally, the proposed framework can be cast as an extension of existing NODE architectures, thereby allowing the use of existing black-box ODE solvers. We prove that the C-NODE framework extends the classical NODE by exhibiting functions that cannot be represented by NODEs but are representable by C-NODEs. We further investigate the efficacy of the C-NODE framework by demonstrating its performance in many synthetic and real data scenarios. Empirical results demonstrate the improvements provided by the proposed method for CIFAR-10, SVHN, and MNIST datasets under a similar computational budget as the existing NODE methods.