LLMForecaster: Improving Seasonal Event Forecasts with Unstructured Textual Data

Modern time-series forecasting models often fail to make full use of rich unstructured information about the time series themselves. This lack of proper conditioning can lead to obvious model failures; for example, models may be unaware of the details of a particular product, and hence fail to anticipate seasonal surges in customer demand in the lead up to major exogenous events like holidays for clearly relevant products. To address this shortcoming, this paper introduces a novel forecast post-processor -- which we call LLMForecaster -- that fine-tunes large language models (LLMs) to incorporate unstructured semantic and contextual information and historical data to improve the forecasts from an existing demand forecasting pipeline. In an industry-scale retail application, we demonstrate that our technique yields statistically significantly forecast improvements across several sets of products subject to holiday-driven demand surges.

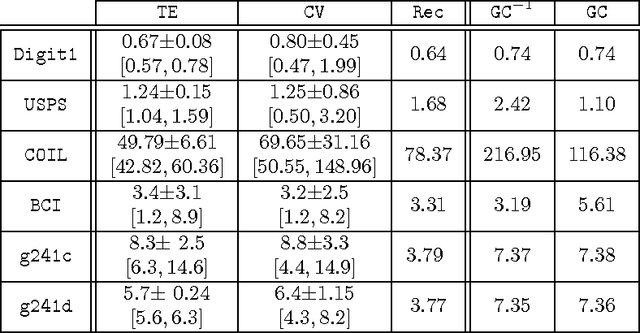
Assessment of Treatment Effect Estimators for Heavy-Tailed Data

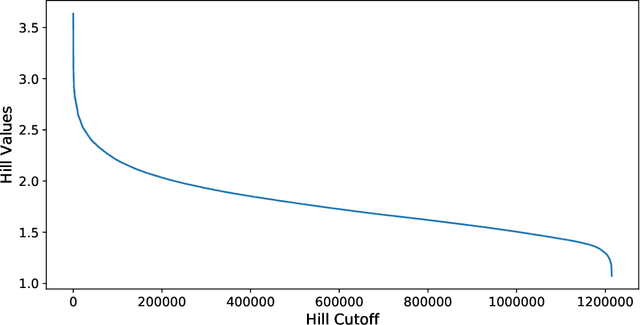
A central obstacle in the objective assessment of treatment effect (TE) estimators in randomized control trials (RCTs) is the lack of ground truth (or validation set) to test their performance. In this paper, we provide a novel cross-validation-like methodology to address this challenge. The key insight of our procedure is that the noisy (but unbiased) difference-of-means estimate can be used as a ground truth "label" on a portion of the RCT, to test the performance of an estimator trained on the other portion. We combine this insight with an aggregation scheme, which borrows statistical strength across a large collection of RCTs, to present an end-to-end methodology for judging an estimator's ability to recover the underlying treatment effect. We evaluate our methodology across 709 RCTs implemented in the Amazon supply chain. In the corpus of AB tests at Amazon, we highlight the unique difficulties associated with recovering the treatment effect due to the heavy-tailed nature of the response variables. In this heavy-tailed setting, our methodology suggests that procedures that aggressively downweight or truncate large values, while introducing bias, lower the variance enough to ensure that the treatment effect is more accurately estimated.

Improved graph Laplacian via geometric self-consistency

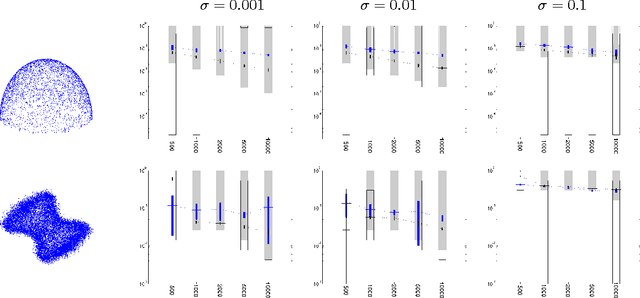
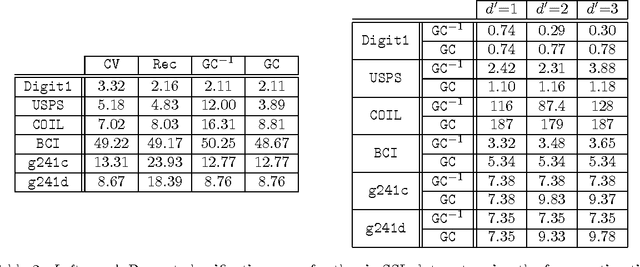
We address the problem of setting the kernel bandwidth used by Manifold Learning algorithms to construct the graph Laplacian. Exploiting the connection between manifold geometry, represented by the Riemannian metric, and the Laplace-Beltrami operator, we set the bandwidth by optimizing the Laplacian's ability to preserve the geometry of the data. Experiments show that this principled approach is effective and robust.

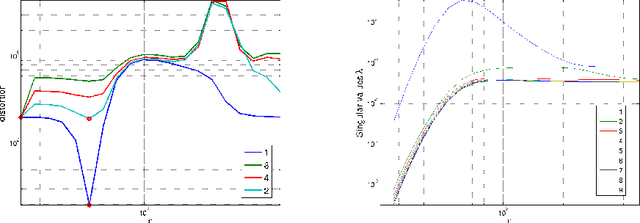
Estimating Vector Fields on Manifolds and the Embedding of Directed Graphs

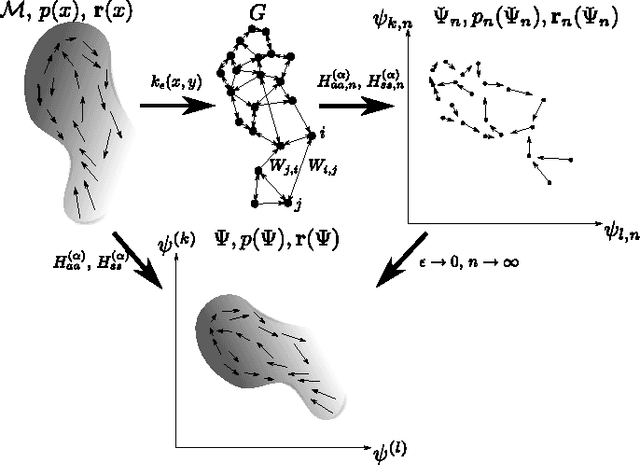
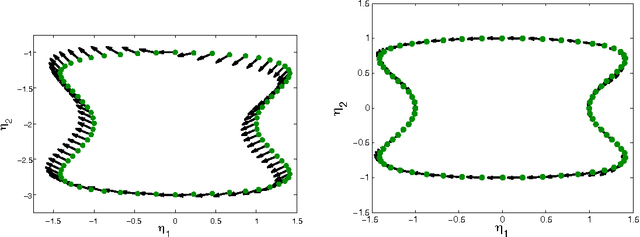
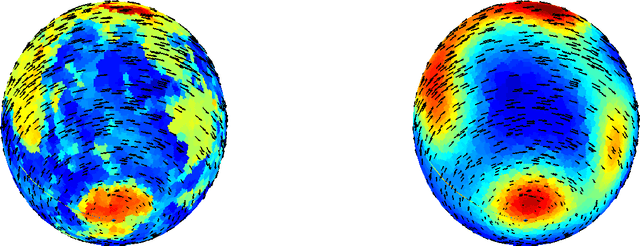
This paper considers the problem of embedding directed graphs in Euclidean space while retaining directional information. We model a directed graph as a finite set of observations from a diffusion on a manifold endowed with a vector field. This is the first generative model of its kind for directed graphs. We introduce a graph embedding algorithm that estimates all three features of this model: the low-dimensional embedding of the manifold, the data density and the vector field. In the process, we also obtain new theoretical results on the limits of "Laplacian type" matrices derived from directed graphs. The application of our method to both artificially constructed and real data highlights its strengths.