Mind the Gap: Examining the Self-Improvement Capabilities of Large Language Models

Self-improvement is a mechanism in Large Language Model (LLM) pre-training, post-training and test-time inference. We explore a framework where the model verifies its own outputs, filters or reweights data based on this verification, and distills the filtered data. Despite several empirical successes, a fundamental understanding is still lacking. In this work, we initiate a comprehensive, modular and controlled study on LLM self-improvement. We provide a mathematical formulation for self-improvement, which is largely governed by a quantity which we formalize as the generation-verification gap. Through experiments with various model families and tasks, we discover a scaling phenomenon of self-improvement -- a variant of the generation-verification gap scales monotonically with the model pre-training flops. We also examine when self-improvement is possible, an iterative self-improvement procedure, and ways to improve its performance. Our findings not only advance understanding of LLM self-improvement with practical implications, but also open numerous avenues for future research into its capabilities and boundaries.

Learning an Inventory Control Policy with General Inventory Arrival Dynamics

In this paper we address the problem of learning and backtesting inventory control policies in the presence of general arrival dynamics -- which we term as a quantity-over-time arrivals model (QOT). We also allow for order quantities to be modified as a post-processing step to meet vendor constraints such as order minimum and batch size constraints -- a common practice in real supply chains. To the best of our knowledge this is the first work to handle either arbitrary arrival dynamics or an arbitrary downstream post-processing of order quantities. Building upon recent work (Madeka et al., 2022) we similarly formulate the periodic review inventory control problem as an exogenous decision process, where most of the state is outside the control of the agent. Madeka et al. (2022) show how to construct a simulator that replays historic data to solve this class of problem. In our case, we incorporate a deep generative model for the arrivals process as part of the history replay. By formulating the problem as an exogenous decision process, we can apply results from Madeka et al. (2022) to obtain a reduction to supervised learning. Finally, we show via simulation studies that this approach yields statistically significant improvements in profitability over production baselines. Using data from an ongoing real-world A/B test, we show that Gen-QOT generalizes well to off-policy data.

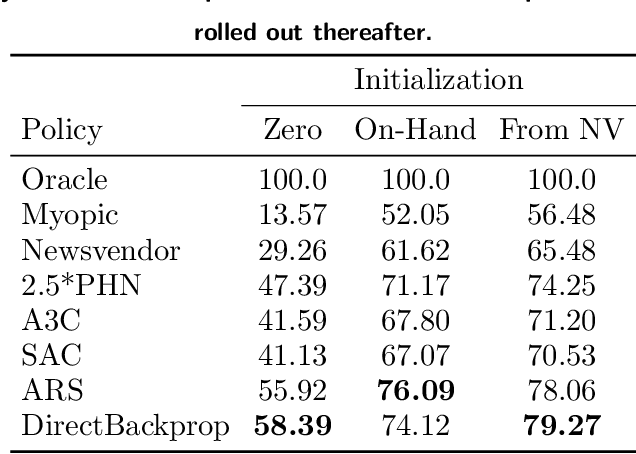
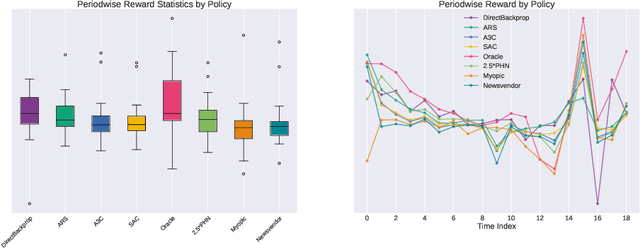
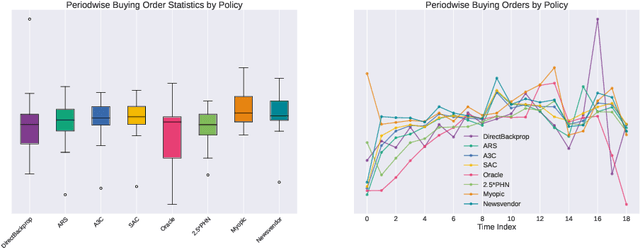
Deep Inventory Management

We present a Deep Reinforcement Learning approach to solving a periodic review inventory control system with stochastic vendor lead times, lost sales, correlated demand, and price matching. While this dynamic program has historically been considered intractable, we show that several policy learning approaches are competitive with or outperform classical baseline approaches. In order to train these algorithms, we develop novel techniques to convert historical data into a simulator. We also present a model-based reinforcement learning procedure (Direct Backprop) to solve the dynamic periodic review inventory control problem by constructing a differentiable simulator. Under a variety of metrics Direct Backprop outperforms model-free RL and newsvendor baselines, in both simulations and real-world deployments.

MQRetNN: Multi-Horizon Time Series Forecasting with Retrieval Augmentation

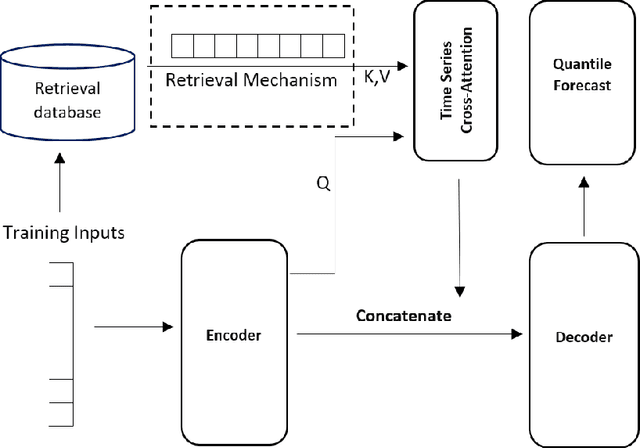
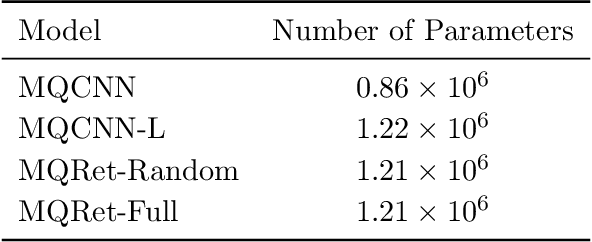
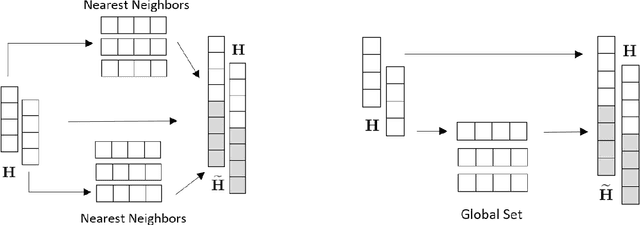
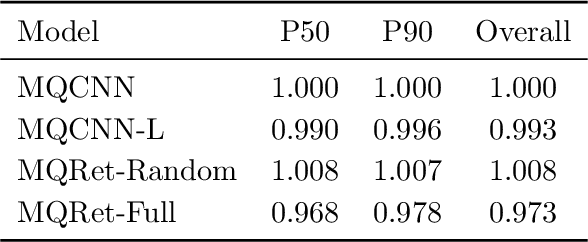
Multi-horizon probabilistic time series forecasting has wide applicability to real-world tasks such as demand forecasting. Recent work in neural time-series forecasting mainly focus on the use of Seq2Seq architectures. For example, MQTransformer - an improvement of MQCNN - has shown the state-of-the-art performance in probabilistic demand forecasting. In this paper, we consider incorporating cross-entity information to enhance model performance by adding a cross-entity attention mechanism along with a retrieval mechanism to select which entities to attend over. We demonstrate how our new neural architecture, MQRetNN, leverages the encoded contexts from a pretrained baseline model on the entire population to improve forecasting accuracy. Using MQCNN as the baseline model (due to computational constraints, we do not use MQTransformer), we first show on a small demand forecasting dataset that it is possible to achieve ~3% improvement in test loss by adding a cross-entity attention mechanism where each entity attends to all others in the population. We then evaluate the model with our proposed retrieval methods - as a means of approximating an attention over a large population - on a large-scale demand forecasting application with over 2 million products and observe ~1% performance gain over the MQCNN baseline.

MQTransformer: Multi-Horizon Forecasts with Context Dependent and Feedback-Aware Attention

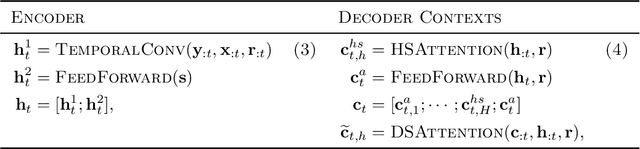
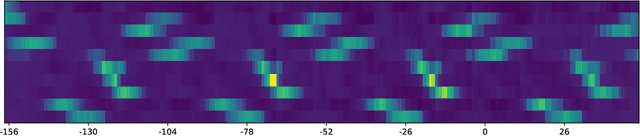
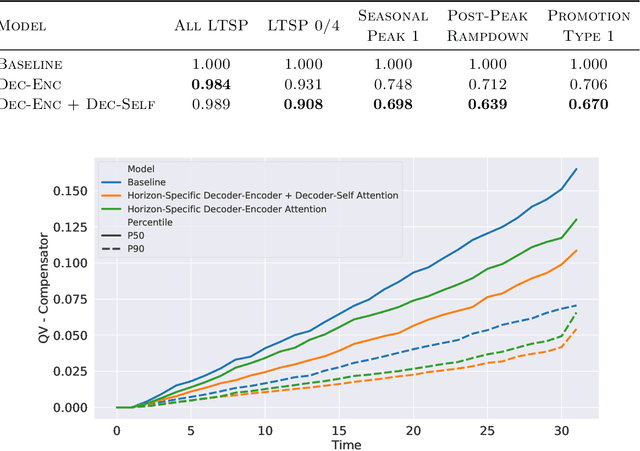
Recent advances in neural forecasting have produced major improvements in accuracy for probabilistic demand prediction. In this work, we propose novel improvements to the current state of the art by incorporating changes inspired by recent advances in Transformer architectures for Natural Language Processing. We develop a novel decoder-encoder attention for context-alignment, improving forecasting accuracy by allowing the network to study its own history based on the context for which it is producing a forecast. We also present a novel positional encoding that allows the neural network to learn context-dependent seasonality functions as well as arbitrary holiday distances. Finally we show that the current state of the art MQ-Forecaster (Wen et al., 2017) models display excess variability by failing to leverage previous errors in the forecast to improve accuracy. We propose a novel decoder-self attention scheme for forecasting that produces significant improvements in the excess variation of the forecast.

Efficient, Certifiably Optimal Clustering with Applications to Latent Variable Graphical Models

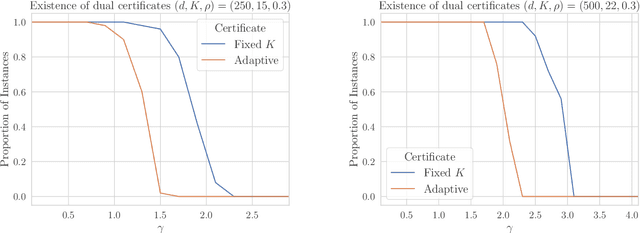
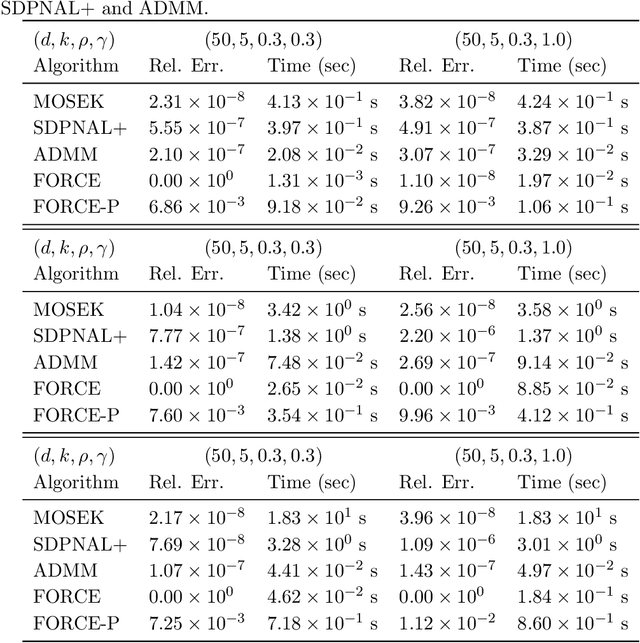
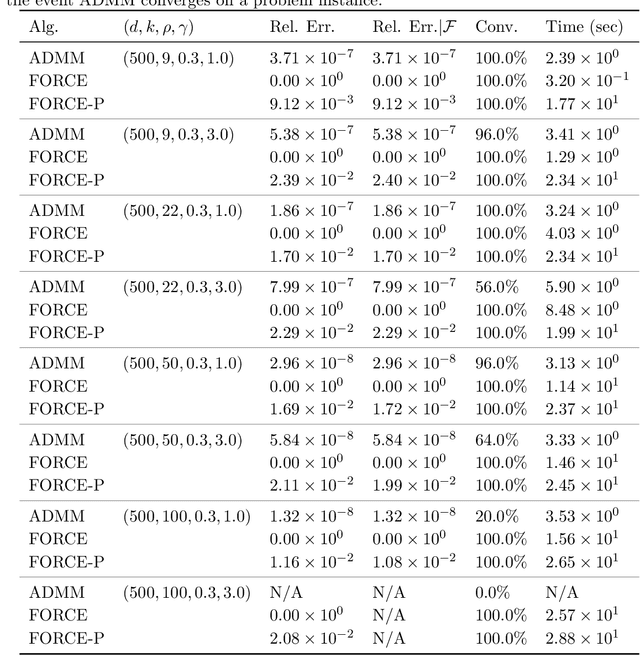
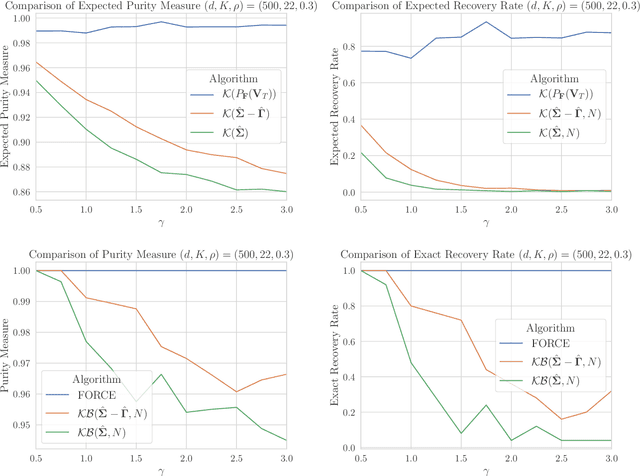
Motivated by the task of clustering either $d$ variables or $d$ points into $K$ groups, we investigate efficient algorithms to solve the Peng-Wei (P-W) $K$-means semi-definite programming (SDP) relaxation. The P-W SDP has been shown in the literature to have good statistical properties in a variety of settings, but remains intractable to solve in practice. To this end we propose FORCE, a new algorithm to solve this SDP relaxation. Compared to the naive interior point method, our method reduces the computational complexity of solving the SDP from $\tilde{O}(d^7\log\epsilon^{-1})$ to $\tilde{O}(d^{6}K^{-2}\epsilon^{-1})$ arithmetic operations for an $\epsilon$-optimal solution. Our method combines a primal first-order method with a dual optimality certificate search, which when successful, allows for early termination of the primal method. We show for certain variable clustering problems that, with high probability, FORCE is guaranteed to find the optimal solution to the SDP relaxation and provide a certificate of exact optimality. As verified by our numerical experiments, this allows FORCE to solve the P-W SDP with dimensions in the hundreds in only tens of seconds. For a variation of the P-W SDP where $K$ is not known a priori a slight modification of FORCE reduces the computational complexity of solving this problem as well: from $\tilde{O}(d^7\log\epsilon^{-1})$ using a standard SDP solver to $\tilde{O}(d^{4}\epsilon^{-1})$.

Marginal Policy Gradients: A Unified Family of Estimators for Bounded Action Spaces with Applications

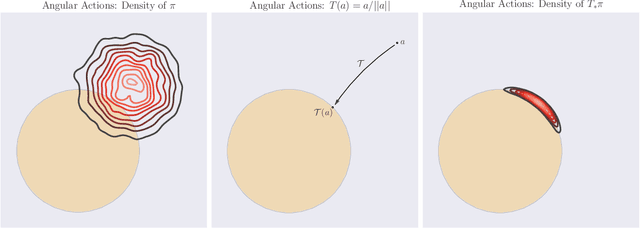
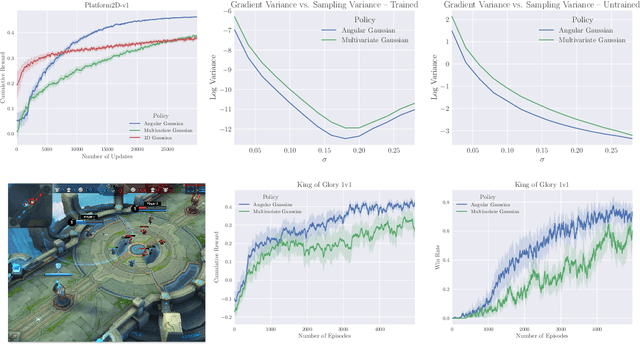
Many complex domains, such as robotics control and real-time strategy (RTS) games, require an agent to learn a continuous control. In the former, an agent learns a policy over $\mathbb{R}^d$ and in the latter, over a discrete set of actions each of which is parametrized by a continuous parameter. Such problems are naturally solved using policy based reinforcement learning (RL) methods, but unfortunately these often suffer from high variance leading to instability and slow convergence. Unnecessary variance is introduced whenever policies over bounded action spaces are modeled using distributions with unbounded support by applying a transformation $T$ to the sampled action before execution in the environment. Recently, the variance reduced clipped action policy gradient (CAPG) was introduced for actions in bounded intervals, but to date no variance reduced methods exist when the action is a direction, something often seen in RTS games. To this end we introduce the angular policy gradient (APG), a stochastic policy gradient method for directional control. With the marginal policy gradients family of estimators we present a unified analysis of the variance reduction properties of APG and CAPG; our results provide a stronger guarantee than existing analyses for CAPG. Experimental results on a popular RTS game and a navigation task show that the APG estimator offers a substantial improvement over the standard policy gradient.

High-Dimensional Inference for Cluster-Based Graphical Models

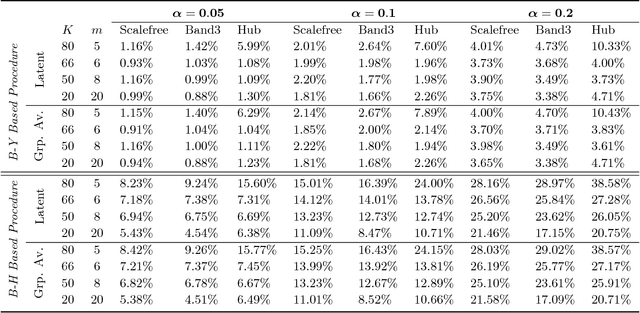
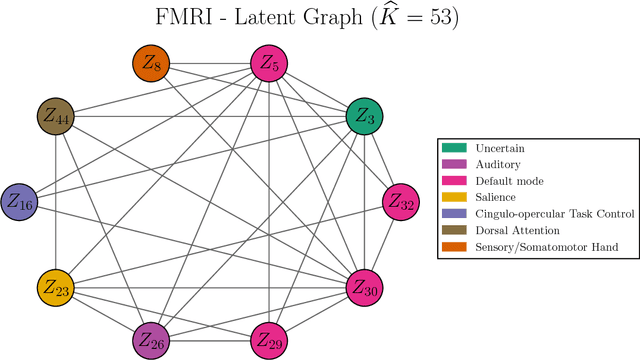
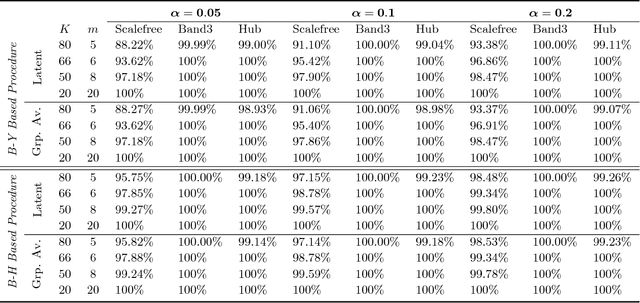
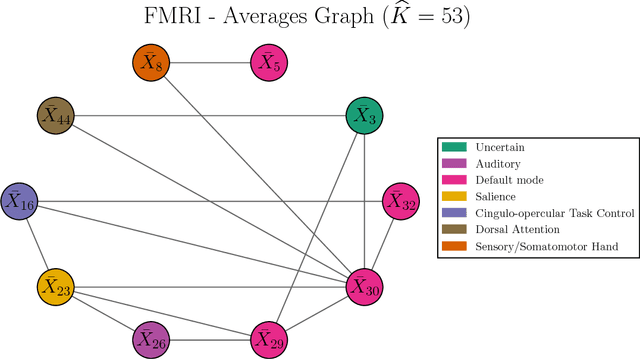
Motivated by modern applications in which one constructs graphical models based on a very large number of features, this paper introduces a new class of cluster-based graphical models. Unlike standard graphical models, variable clustering is applied as an initial step for reducing the dimension of the feature space. We employ model assisted clustering, in which the clusters contain features that are similar to the same unobserved latent variable. Two different cluster-based Gaussian graphical models are considered: the latent variable graph, corresponding to the graphical model associated with the unobserved latent variables, and the cluster-average graph, corresponding to the vector of features averaged over clusters. We derive estimates tailored to these graphs, with the goal of pattern recovery under false discovery rate (FDR) control. Our study reveals that likelihood based inference for the latent graph is analytically intractable, and we develop alternative estimation and inference strategies. We replace the likelihood of the data by appropriate empirical risk functions that allow for valid inference in both graphical models under study. Our main results are Berry-Esseen central limit theorems for the proposed estimators, which are proved under weaker assumptions than those employed in the existing literature on Gaussian graphical model inference. We make explicit the implications of the asymptotic approximations on graph recovery under FDR control, and show when it can be controlled asymptotically. Our analysis takes into account the uncertainty induced by the initial clustering step. We find that the errors induced by clustering are asymptotically ignorable in the follow-up analysis, under no further restrictions on the parameter space for which inference is valid. The theoretical properties of the proposed procedures are verified on simulated data and an fMRI data analysis.