Learning an Inventory Control Policy with General Inventory Arrival Dynamics

In this paper we address the problem of learning and backtesting inventory control policies in the presence of general arrival dynamics -- which we term as a quantity-over-time arrivals model (QOT). We also allow for order quantities to be modified as a post-processing step to meet vendor constraints such as order minimum and batch size constraints -- a common practice in real supply chains. To the best of our knowledge this is the first work to handle either arbitrary arrival dynamics or an arbitrary downstream post-processing of order quantities. Building upon recent work (Madeka et al., 2022) we similarly formulate the periodic review inventory control problem as an exogenous decision process, where most of the state is outside the control of the agent. Madeka et al. (2022) show how to construct a simulator that replays historic data to solve this class of problem. In our case, we incorporate a deep generative model for the arrivals process as part of the history replay. By formulating the problem as an exogenous decision process, we can apply results from Madeka et al. (2022) to obtain a reduction to supervised learning. Finally, we show via simulation studies that this approach yields statistically significant improvements in profitability over production baselines. Using data from an ongoing real-world A/B test, we show that Gen-QOT generalizes well to off-policy data.

Contextual Bandits for Evaluating and Improving Inventory Control Policies

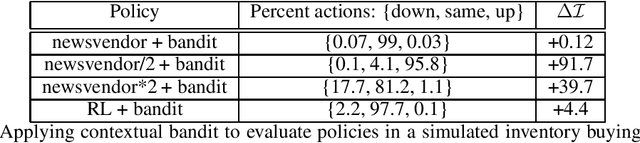
Solutions to address the periodic review inventory control problem with nonstationary random demand, lost sales, and stochastic vendor lead times typically involve making strong assumptions on the dynamics for either approximation or simulation, and applying methods such as optimization, dynamic programming, or reinforcement learning. Therefore, it is important to analyze and evaluate any inventory control policy, in particular to see if there is room for improvement. We introduce the concept of an equilibrium policy, a desirable property of a policy that intuitively means that, in hindsight, changing only a small fraction of actions does not result in materially more reward. We provide a light-weight contextual bandit-based algorithm to evaluate and occasionally tweak policies, and show that this method achieves favorable guarantees, both theoretically and in empirical studies.

Linear Reinforcement Learning with Ball Structure Action Space

We study the problem of Reinforcement Learning (RL) with linear function approximation, i.e. assuming the optimal action-value function is linear in a known $d$-dimensional feature mapping. Unfortunately, however, based on only this assumption, the worst case sample complexity has been shown to be exponential, even under a generative model. Instead of making further assumptions on the MDP or value functions, we assume that our action space is such that there always exist playable actions to explore any direction of the feature space. We formalize this assumption as a ``ball structure'' action space, and show that being able to freely explore the feature space allows for efficient RL. In particular, we propose a sample-efficient RL algorithm (BallRL) that learns an $\epsilon$-optimal policy using only $\tilde{O}\left(\frac{H^5d^3}{\epsilon^3}\right)$ number of trajectories.

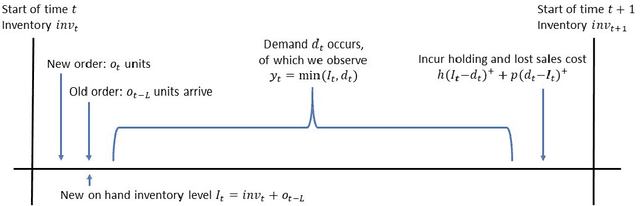
Learning in structured MDPs with convex cost functions: Improved regret bounds for inventory management

We consider a stochastic inventory control problem under censored demands, lost sales, and positive lead times. This is a fundamental problem in inventory management, with significant literature establishing near-optimality of a simple class of policies called ``base-stock policies'' for the underlying Markov Decision Process (MDP), as well as convexity of long run average-cost under those policies. We consider the relatively less studied problem of designing a learning algorithm for this problem when the underlying demand distribution is unknown. The goal is to bound regret of the algorithm when compared to the best base-stock policy. We utilize the convexity properties and a newly derived bound on bias of base-stock policies to establish a connection to stochastic convex bandit optimization. Our main contribution is a learning algorithm with a regret bound of $\tilde{O}(L\sqrt{T}+D)$ for the inventory control problem. Here $L$ is the fixed and known lead time, and $D$ is an unknown parameter of the demand distribution described roughly as the number of time steps needed to generate enough demand for depleting one unit of inventory. Notably, even though the state space of the underlying MDP is continuous and $L$-dimensional, our regret bounds depend linearly on $L$. Our results significantly improve the previously best known regret bounds for this problem where the dependence on $L$ was exponential and many further assumptions on demand distribution were required. The techniques presented here may be of independent interest for other settings that involve large structured MDPs but with convex cost functions.

Posterior sampling for reinforcement learning: worst-case regret bounds

We present an algorithm based on posterior sampling (aka Thompson sampling) that achieves near-optimal worst-case regret bounds when the underlying Markov Decision Process (MDP) is communicating with a finite, though unknown, diameter. Our main result is a high probability regret upper bound of $\tilde{O}(D\sqrt{SAT})$ for any communicating MDP with $S$ states, $A$ actions and diameter $D$, when $T\ge S^5A$. Here, regret compares the total reward achieved by the algorithm to the total expected reward of an optimal infinite-horizon undiscounted average reward policy, in time horizon $T$. This result improves over the best previously known upper bound of $\tilde{O}(DS\sqrt{AT})$ achieved by any algorithm in this setting, and matches the dependence on $S$ in the established lower bound of $\Omega(\sqrt{DSAT})$ for this problem. Our techniques involve proving some novel results about the anti-concentration of Dirichlet distribution, which may be of independent interest.