On the Complexity of Multi-Agent Decision Making: From Learning in Games to Partial Monitoring

A central problem in the theory of multi-agent reinforcement learning (MARL) is to understand what structural conditions and algorithmic principles lead to sample-efficient learning guarantees, and how these considerations change as we move from few to many agents. We study this question in a general framework for interactive decision making with multiple agents, encompassing Markov games with function approximation and normal-form games with bandit feedback. We focus on equilibrium computation, in which a centralized learning algorithm aims to compute an equilibrium by controlling multiple agents that interact with an unknown environment. Our main contributions are: - We provide upper and lower bounds on the optimal sample complexity for multi-agent decision making based on a multi-agent generalization of the Decision-Estimation Coefficient, a complexity measure introduced by Foster et al. (2021) in the single-agent counterpart to our setting. Compared to the best results for the single-agent setting, our bounds have additional gaps. We show that no "reasonable" complexity measure can close these gaps, highlighting a striking separation between single and multiple agents. - We show that characterizing the statistical complexity for multi-agent decision making is equivalent to characterizing the statistical complexity of single-agent decision making, but with hidden (unobserved) rewards, a framework that subsumes variants of the partial monitoring problem. As a consequence, we characterize the statistical complexity for hidden-reward interactive decision making to the best extent possible. Building on this development, we provide several new structural results, including 1) conditions under which the statistical complexity of multi-agent decision making can be reduced to that of single-agent, and 2) conditions under which the so-called curse of multiple agents can be avoided.

Linear Reinforcement Learning with Ball Structure Action Space

We study the problem of Reinforcement Learning (RL) with linear function approximation, i.e. assuming the optimal action-value function is linear in a known $d$-dimensional feature mapping. Unfortunately, however, based on only this assumption, the worst case sample complexity has been shown to be exponential, even under a generative model. Instead of making further assumptions on the MDP or value functions, we assume that our action space is such that there always exist playable actions to explore any direction of the feature space. We formalize this assumption as a ``ball structure'' action space, and show that being able to freely explore the feature space allows for efficient RL. In particular, we propose a sample-efficient RL algorithm (BallRL) that learns an $\epsilon$-optimal policy using only $\tilde{O}\left(\frac{H^5d^3}{\epsilon^3}\right)$ number of trajectories.

Forecast Hedging and Calibration

Calibration means that forecasts and average realized frequencies are close. We develop the concept of forecast hedging, which consists of choosing the forecasts so as to guarantee that the expected track record can only improve. This yields all the calibration results by the same simple basic argument while differentiating between them by the forecast-hedging tools used: deterministic and fixed point based versus stochastic and minimax based. Additional contributions are an improved definition of continuous calibration, ensuing game dynamics that yield Nash equilibria in the long run, and a new calibrated forecasting procedure for binary events that is simpler than all known such procedures.

Smooth Calibration, Leaky Forecasts, Finite Recall, and Nash Dynamics

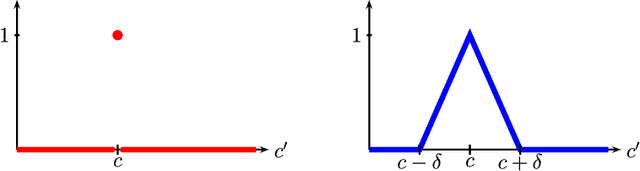
We propose to smooth out the calibration score, which measures how good a forecaster is, by combining nearby forecasts. While regular calibration can be guaranteed only by randomized forecasting procedures, we show that smooth calibration can be guaranteed by deterministic procedures. As a consequence, it does not matter if the forecasts are leaked, i.e., made known in advance: smooth calibration can nevertheless be guaranteed (while regular calibration cannot). Moreover, our procedure has finite recall, is stationary, and all forecasts lie on a finite grid. To construct the procedure, we deal also with the related setups of online linear regression and weak calibration. Finally, we show that smooth calibration yields uncoupled finite-memory dynamics in n-person games "smooth calibrated learning" in which the players play approximate Nash equilibria in almost all periods (by contrast, calibrated learning, which uses regular calibration, yields only that the time-averages of play are approximate correlated equilibria).

"Calibeating": Beating Forecasters at Their Own Game

In order to identify expertise, forecasters should not be tested by their calibration score, which can always be made arbitrarily small, but rather by their Brier score. The Brier score is the sum of the calibration score and the refinement score; the latter measures how good the sorting into bins with the same forecast is, and thus attests to "expertise." This raises the question of whether one can gain calibration without losing expertise, which we refer to as "calibeating." We provide an easy way to calibeat any forecast, by a deterministic online procedure. We moreover show that calibeating can be achieved by a stochastic procedure that is itself calibrated, and then extend the results to simultaneously calibeating multiple procedures, and to deterministic procedures that are continuously calibrated.

A Few Expert Queries Suffices for Sample-Efficient RL with Resets and Linear Value Approximation

The current paper studies sample-efficient Reinforcement Learning (RL) in settings where only the optimal value function is assumed to be linearly-realizable. It has recently been understood that, even under this seemingly strong assumption and access to a generative model, worst-case sample complexities can be prohibitively (i.e., exponentially) large. We investigate the setting where the learner additionally has access to interactive demonstrations from an expert policy, and we present a statistically and computationally efficient algorithm (Delphi) for blending exploration with expert queries. In particular, Delphi requires $\tilde{\mathcal{O}}(d)$ expert queries and a $\texttt{poly}(d,H,|\mathcal{A}|,1/\varepsilon)$ amount of exploratory samples to provably recover an $\varepsilon$-suboptimal policy. Compared to pure RL approaches, this corresponds to an exponential improvement in sample complexity with surprisingly-little expert input. Compared to prior imitation learning (IL) approaches, our required number of expert demonstrations is independent of $H$ and logarithmic in $1/\varepsilon$, whereas all prior work required at least linear factors of both in addition to the same dependence on $d$. Towards establishing the minimal amount of expert queries needed, we show that, in the same setting, any learner whose exploration budget is polynomially-bounded (in terms of $d,H,$ and $|\mathcal{A}|$) will require at least $\tilde\Omega(\sqrt{d})$ oracle calls to recover a policy competing with the expert's value function. Under the weaker assumption that the expert's policy is linear, we show that the lower bound increases to $\tilde\Omega(d)$.

On Submodular Contextual Bandits

We consider the problem of contextual bandits where actions are subsets of a ground set and mean rewards are modeled by an unknown monotone submodular function that belongs to a class $\mathcal{F}$. We allow time-varying matroid constraints to be placed on the feasible sets. Assuming access to an online regression oracle with regret $\mathsf{Reg}(\mathcal{F})$, our algorithm efficiently randomizes around local optima of estimated functions according to the Inverse Gap Weighting strategy. We show that cumulative regret of this procedure with time horizon $n$ scales as $O(\sqrt{n \mathsf{Reg}(\mathcal{F})})$ against a benchmark with a multiplicative factor $1/2$. On the other hand, using the techniques of (Filmus and Ward 2014), we show that an $\epsilon$-Greedy procedure with local randomization attains regret of $O(n^{2/3} \mathsf{Reg}(\mathcal{F})^{1/3})$ against a stronger $(1-e^{-1})$ benchmark.

The Benefits of Implicit Regularization from SGD in Least Squares Problems

Stochastic gradient descent (SGD) exhibits strong algorithmic regularization effects in practice, which has been hypothesized to play an important role in the generalization of modern machine learning approaches. In this work, we seek to understand these issues in the simpler setting of linear regression (including both underparameterized and overparameterized regimes), where our goal is to make sharp instance-based comparisons of the implicit regularization afforded by (unregularized) average SGD with the explicit regularization of ridge regression. For a broad class of least squares problem instances (that are natural in high-dimensional settings), we show: (1) for every problem instance and for every ridge parameter, (unregularized) SGD, when provided with logarithmically more samples than that provided to the ridge algorithm, generalizes no worse than the ridge solution (provided SGD uses a tuned constant stepsize); (2) conversely, there exist instances (in this wide problem class) where optimally-tuned ridge regression requires quadratically more samples than SGD in order to have the same generalization performance. Taken together, our results show that, up to the logarithmic factors, the generalization performance of SGD is always no worse than that of ridge regression in a wide range of overparameterized problems, and, in fact, could be much better for some problem instances. More generally, our results show how algorithmic regularization has important consequences even in simpler (overparameterized) convex settings.

Threshold Martingales and the Evolution of Forecasts

This paper introduces a martingale that characterizes two properties of evolving forecast distributions. Ideal forecasts of a future event behave as martingales, sequen- tially updating the forecast to leverage the available information as the future event approaches. The threshold martingale introduced here measures the proportion of the forecast distribution lying below a threshold. In addition to being calibrated, a threshold martingale has quadratic variation that accumulates to a total determined by a quantile of the initial forecast distribution. Deviations from calibration or to- tal volatility signal problems in the underlying model. Calibration adjustments are well-known, and we augment these by introducing a martingale filter that improves volatility while guaranteeing smaller mean squared error. Thus, post-processing can rectify problems with calibration and volatility without revisiting the original forecast- ing model. We apply threshold martingales first to forecasts from simulated models and then to models that predict the winner in professional basketball games.

What are the Statistical Limits of Offline RL with Linear Function Approximation?

Offline reinforcement learning seeks to utilize offline (observational) data to guide the learning of (causal) sequential decision making strategies. The hope is that offline reinforcement learning coupled with function approximation methods (to deal with the curse of dimensionality) can provide a means to help alleviate the excessive sample complexity burden in modern sequential decision making problems. However, the extent to which this broader approach can be effective is not well understood, where the literature largely consists of sufficient conditions. This work focuses on the basic question of what are necessary representational and distributional conditions that permit provable sample-efficient offline reinforcement learning. Perhaps surprisingly, our main result shows that even if: i) we have realizability in that the true value function of \emph{every} policy is linear in a given set of features and 2) our off-policy data has good coverage over all features (under a strong spectral condition), then any algorithm still (information-theoretically) requires a number of offline samples that is exponential in the problem horizon in order to non-trivially estimate the value of \emph{any} given policy. Our results highlight that sample-efficient offline policy evaluation is simply not possible unless significantly stronger conditions hold; such conditions include either having low distribution shift (where the offline data distribution is close to the distribution of the policy to be evaluated) or significantly stronger representational conditions (beyond realizability).